最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
つり合い式の基本的な弱形式は,式(D.7)のつり合い式から
と書くことができるから,部分積分をして境界条件式(D.8)を代入すると
となる。これに式(D.3)を
考慮して式(D.5)を代入すると,最終的な仮想仕事式
が
となる。内力仮想仕事項は式(D.3)を考慮すると
とも表すことができる。
式(D.12)を見る限り![]() は要素内一定,
は要素内一定,![]() は1次
多項式でよさそうだ。
したがって式(D.3)を考慮すれば
は1次
多項式でよさそうだ。
したがって式(D.3)を考慮すれば![]() には2次多項式で
いいことになる。
これで四つの未定係数で
には2次多項式で
いいことになる。
これで四つの未定係数で![]() ,
, ![]() を表すことができ,節点での
連続条件を満足すべき四つの
を表すことができ,節点での
連続条件を満足すべき四つの![]() ,
, ![]() を係数とする
変位関数が仮定できる。
しかし式(D.13)を見ると,
これでは被積分関数第2項の
を係数とする
変位関数が仮定できる。
しかし式(D.13)を見ると,
これでは被積分関数第2項の![]() の微係数が落ちてしまう。
だからといって
の微係数が落ちてしまう。
だからといって![]() に1次の多項式を仮定すると
未定係数の数が一つ増え,
後述の高次要素と同じような煩雑さを伴う。
ただこの第2項は曲げの項であり,
に1次の多項式を仮定すると
未定係数の数が一つ増え,
後述の高次要素と同じような煩雑さを伴う。
ただこの第2項は曲げの項であり,![]() の貢献は
主に第1項であろうから,
思い切ってこの最も簡単な変位関数を採用して試してみよう。
つまり
の貢献は
主に第1項であろうから,
思い切ってこの最も簡単な変位関数を採用して試してみよう。
つまり
と置く。これを式(D.13)に代入して剛性行列
を求めると
となる。
ところでTimoshenko梁理論はBernoulli-Euler梁の拡張理論で
あり,![]() の極限で各基礎式は初等梁理論のそれに整合する
はずである。しかし式(D.14)の剛性
行列は,
の極限で各基礎式は初等梁理論のそれに整合する
はずである。しかし式(D.14)の剛性
行列は,![]() の極限で式(5.24)にはならない。
しかも式(D.14)を用いた有限要素解析による
数値解は,要素数を非常に多く用いなければならない等,
厳密解への収束が非常に遅い[38]こともわかっている。
の極限で式(5.24)にはならない。
しかも式(D.14)を用いた有限要素解析による
数値解は,要素数を非常に多く用いなければならない等,
厳密解への収束が非常に遅い[38]こともわかっている。
たわみ![]() で表したつり合い式(D.9)を見ると
明らかなように,最も重要な項は初等梁理論と同様,たわみ
についての4階の微係数であった。したがって,
で表したつり合い式(D.9)を見ると
明らかなように,最も重要な項は初等梁理論と同様,たわみ
についての4階の微係数であった。したがって,![]() に対しては3次の
多項式を用いるのが望ましいことは明らかであったが,前節では
故意に簡単な要素を誘導してみた。
そこでここでは,
に対しては3次の
多項式を用いるのが望ましいことは明らかであったが,前節では
故意に簡単な要素を誘導してみた。
そこでここでは,![]() については定数として
については定数として
と置いてみよう。ここに![]() は式(5.21)で定義した
多項式であり,新たに
は式(5.21)で定義した
多項式であり,新たに
と定義した。
ここでも![]() を定数と置いているから,式(D.13)の
被積分関数第2項の
を定数と置いているから,式(D.13)の
被積分関数第2項の![]() の微係数が落ちてしまう。しかし,
式(D.15)の
の微係数が落ちてしまう。しかし,
式(D.15)の![]() の方の
変位関数表現に
の方の
変位関数表現に![]() の項があることから,
少なからずせん断変形の影響がこの第2項にも及ぶことが期待できる。
また
の項があることから,
少なからずせん断変形の影響がこの第2項にも及ぶことが期待できる。
また![]() を1次多項式にしても,実は求められる剛性方程式が同じに
なることは,ちょっと面倒な演算で示すことができる。
を1次多項式にしても,実は求められる剛性方程式が同じに
なることは,ちょっと面倒な演算で示すことができる。
式(D.15)を式(D.12)に代入して「要素」剛性方程式を
求めると
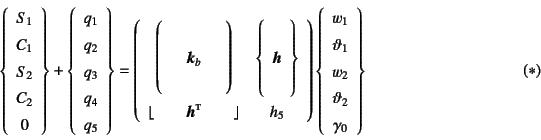
となる。
なお簡単のためにこの章では,括弧無しの太字で行列を表している。
ここで![]() は式(5.22a) (5.24)で
定義された初等梁の剛性行列であり,
は式(5.22a) (5.24)で
定義された初等梁の剛性行列であり,![]() (
(![]() =1〜4)は
式(5.22b)で定義された等価節点外力である。
=1〜4)は
式(5.22b)で定義された等価節点外力である。![]() や
や![]() の
具体的な表現は省略するが
の
具体的な表現は省略するが
と定義した。なお簡単のためにこの章では括弧無しの太字で行列を
表している。剛性方程式(![]() )の第5行目の式は,境界条件から判断して
左辺の外力に相当する部分が零になっており,これは要素剛性方程式の
レベルでの余剰な自由度
)の第5行目の式は,境界条件から判断して
左辺の外力に相当する部分が零になっており,これは要素剛性方程式の
レベルでの余剰な自由度![]() に対する付帯条件と
考えなければならない。つまり式(D.8)の境界条件
から判断して
に対する付帯条件と
考えなければならない。つまり式(D.8)の境界条件
から判断して![]() は要素間で連続になる必要が無いから,
式(
は要素間で連続になる必要が無いから,
式(![]() )の形で
)の形で![]() を剛性方程式に残しておく必要はなくなる。
したがって,式(
を剛性方程式に残しておく必要はなくなる。
したがって,式(![]() )第5行目から
)第5行目から![]() を計算してしまい,
それを残りの行に代入して剛性行列の縮約を行う。第5行目の式は
を計算してしまい,
それを残りの行に代入して剛性行列の縮約を行う。第5行目の式は
となる。便宜上
と置いた。式(![]() )を式(
)を式(![]() )の上4行右辺に代入すると
)の上4行右辺に代入すると
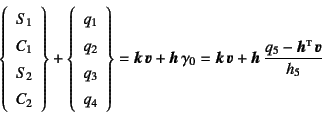
であり,
![]() は式(4.85a)で定義したパラメータ
である。
この
は式(4.85a)で定義したパラメータ
である。
この
![]() がせん断変形の影響の程度を代表するパラメータであり,
せん断変形を無視する場合には前述のように
せん断抵抗係数
がせん断変形の影響の程度を代表するパラメータであり,
せん断変形を無視する場合には前述のように
せん断抵抗係数![]() と考えればいいから,
と考えればいいから,
![]() と
なる。
と
なる。
![]() のとき,式(D.18c)は
式(5.24)の初等梁理論の剛性行列に一致する。
実は式(D.17)はマトリックス構造解析
の基礎式としての
厳密な剛性方程式に一致する。したがって当然のことであるが,
式(D.9) (D.10)で表した支配方程式から
有限要素定式化しても同じ剛性方程式(D.17)が求められる。
この節を高次要素と題したが,以上のような意味ではこの要素の方が
有限要素法として適正なものと言えよう。
のとき,式(D.18c)は
式(5.24)の初等梁理論の剛性行列に一致する。
実は式(D.17)はマトリックス構造解析
の基礎式としての
厳密な剛性方程式に一致する。したがって当然のことであるが,
式(D.9) (D.10)で表した支配方程式から
有限要素定式化しても同じ剛性方程式(D.17)が求められる。
この節を高次要素と題したが,以上のような意味ではこの要素の方が
有限要素法として適正なものと言えよう。