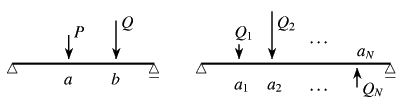 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
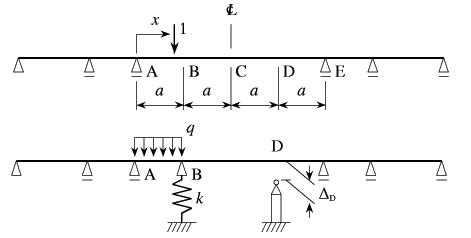
章-2では,静定トラスと静定梁を設計するときに,
断面力の影響線を求めなければ荷重の位置を決めることができないことを説明した。
つまり,構造設計で最初に必要になる4.8のはそういった影響線だ。
ここではたわみの影響線を中心にして説明する。
例えば図-4.50の系Bのように,ある点![]() に
単位の大きさの集中外力が作用している問題の解を
に
単位の大きさの集中外力が作用している問題の解を![]() と
記すことにしたので,章-4.3でも用いた
線形系の重ね合わせの原理から,
同じ点に大きさ
と
記すことにしたので,章-4.3でも用いた
線形系の重ね合わせの原理から,
同じ点に大きさ![]() の集中外力が作用した問題の解は
の集中外力が作用した問題の解は![]() と
なる。さらに,点
と
なる。さらに,点![]() にも大きさ
にも大きさ![]() の集中外力が
作用しているような場合にはたわみが
の集中外力が
作用しているような場合にはたわみが
![]() に
なるのも自明であろう。
つまり,ある点
に
なるのも自明であろう。
つまり,ある点![]() ,
,
![]() に集中外力
に集中外力![]() が
作用している場合の解は
が
作用している場合の解は
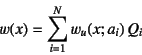
でいいことになる(図-4.53参照)。
では次に,任意の分布外力![]() が作用している場合に,
ある観測点
が作用している場合に,
ある観測点![]() で発生するたわみを計算することを考えよう。
この場合は図-4.54に示したように,梁の全長を
で発生するたわみを計算することを考えよう。
この場合は図-4.54に示したように,梁の全長を![]() 等分
したとして,ある点
等分
したとして,ある点![]() 近傍の分布外力を集中外力で
近似してみよう。前節でも示したように,集中外力は面積がその大きさに
なるような非常に短い区間に作用する分布外力としてもモデル化できた
ことから,この点
近傍の分布外力を集中外力で
近似してみよう。前節でも示したように,集中外力は面積がその大きさに
なるような非常に短い区間に作用する分布外力としてもモデル化できた
ことから,この点![]() 近傍の集中外力
近傍の集中外力![]() は
は
![]() と
置いてもいいだろう。
したがって,もし上で使ったような
と
置いてもいいだろう。
したがって,もし上で使ったような![]() が
既知であれば,ある点
が
既知であれば,ある点![]() のたわみは
のたわみは
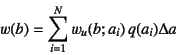
でいいことになる。これに数学的極限としての![]() を考えると,
この総和を積分に置き換えればいいだけである
を考えると,
この総和を積分に置き換えればいいだけである
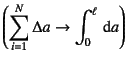 から,結局
から,結局
によって点![]() におけるたわみを求めることができる。
におけるたわみを求めることができる。
このように![]() は「載荷点
は「載荷点![]() に作用する単位外力が,観測
点
に作用する単位外力が,観測
点![]() のたわみにどの程度の影響を与えるか」を定量的に示した関数で
あることから,この観測点
のたわみにどの程度の影響を与えるか」を定量的に示した関数で
あることから,この観測点![]() におけるたわみの影響線
と呼ばれている。ある着目点の断面を設計するに当たっては,
その点での応答が一番大きく(不利に)なるような外力の
載せ方をまず知る必要があるが,そのような場合に影響線が必要になることは
既に述べた。
数学では
におけるたわみの影響線
と呼ばれている。ある着目点の断面を設計するに当たっては,
その点での応答が一番大きく(不利に)なるような外力の
載せ方をまず知る必要があるが,そのような場合に影響線が必要になることは
既に述べた。
数学では![]() のような関数を,対象としている
境界値問題のGreen関数
と呼んでいる。これは材料力学の
多くの問題を解析的に,あるいは半解析的に解く場合に
重用される概念であり,数値解析手法の一つと
しての境界要素法
においても(そちらは基本解
ではあるが)非常に重要な概念である。
昨今は数値的なシミュレーションが全盛で,解析的な手法や考察がないがしろに
されることが多いように感じる。しかし,数値シミュレーションは
単なるケーススタディにしか過ぎず,対象としている問題全体が持っている
力学的特性を定性的かつ定量的に把握できるとは限らない。
そういう観点から,このGreen関数等の特性を考えると,
設計という観点から見ても有用なことを多く含んでいると感じられる。
のような関数を,対象としている
境界値問題のGreen関数
と呼んでいる。これは材料力学の
多くの問題を解析的に,あるいは半解析的に解く場合に
重用される概念であり,数値解析手法の一つと
しての境界要素法
においても(そちらは基本解
ではあるが)非常に重要な概念である。
昨今は数値的なシミュレーションが全盛で,解析的な手法や考察がないがしろに
されることが多いように感じる。しかし,数値シミュレーションは
単なるケーススタディにしか過ぎず,対象としている問題全体が持っている
力学的特性を定性的かつ定量的に把握できるとは限らない。
そういう観点から,このGreen関数等の特性を考えると,
設計という観点から見ても有用なことを多く含んでいると感じられる。
簡単のために,観測点が![]() の単純梁を対象として式(4.61)を
証明しておく。解きたい問題は,
ある与えられた分布外力の作用した単純梁なので
の単純梁を対象として式(4.61)を
証明しておく。解きたい問題は,
ある与えられた分布外力の作用した単純梁なので
がつり合い式で,境界条件は
で与えられているものとする。
一方,図-4.55に
示した左の系Aのたわみ![]() は観測点
は観測点![]() に単位集中荷重を載せた系で
に単位集中荷重を載せた系で
を満足しており,![]() の境界条件は上式(b)と同じである。
影響線を求める系は同じく図-4.55の右の系Bのように
任意の点
の境界条件は上式(b)と同じである。
影響線を求める系は同じく図-4.55の右の系Bのように
任意の点![]() に単位集中荷重を載せた系でで
あり,そのたわみ
に単位集中荷重を載せた系でで
あり,そのたわみ![]() も同じ境界条件の元で
も同じ境界条件の元で
を満足しているものとする。系Aは系Bの随伴系 と呼ばれている。
ここで,単位荷重法の誘導と同じように式(c)に
求めたい解![]() を乗じて全領域で積分し(仮想仕事を算定し),
デルタ関数の定義を用いることにすると
を乗じて全領域で積分し(仮想仕事を算定し),
デルタ関数の定義を用いることにすると
となる。さらに,右辺第1項を移項してそれを4回部分積分すると
![\begin{eqnarray*}
w(b)&=&\int_0^\ell EI{w_u^*}''''(x;b) w(x) \dint x \\
&=& \le...
...)\right] \Bigr\vert _0^\ell
-\int_0^\ell w_u^*(-EIw'''')\dint x
\end{eqnarray*}](s1img1438.gif)
を得る。これに境界条件を代入すれば右辺第1, 2項の境界での
値はすべて零になり,
第3項の被積分関数の括弧の中は式(a)より![]() なので
なので
となる。
次に式(c)に影響線![]() の方を乗じて
全領域で積分すると,同様に
の方を乗じて
全領域で積分すると,同様に
となるので,これも4回部分積分すると最終的に
を得ることができる。この関係はちょっと面白い。
つまり図-4.55を見ると理解し易くなるが,
「ある構造物の,ある載荷点に単位荷重を載せたときに別のある観測点で観測された
たわみは,逆にその観測点に単位荷重を載せて観測される元の載荷点の
たわみに等しくなる」ということである。
これをMaxwellの相反定理
と呼ぶ。さて,上式の記号![]() を
を![]() に置き換えた上で
式(e)の右辺に代入すると
に置き換えた上で
式(e)の右辺に代入すると
となり,式(4.61)が証明された。
ちなみに,図-4.55の荷重を一般化し,系Aには![]() が
作用してたわみ
が
作用してたわみ![]() が生じ,系Bには
が生じ,系Bには![]() が作用してたわみ
が作用してたわみ![]() が
生じたとすると,
上述と同様の演算から式(4.62)の代わりに
が
生じたとすると,
上述と同様の演算から式(4.62)の代わりに
を得る。これはBettiの相反定理 と呼ばれる。 相反定理の誘導にはエネルギ等の物理的解釈(自己随伴系 にしか使えないし,そもそも本末転倒の間違った誘導・証明だ)は要らない。
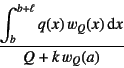
となることを示せ。相反定理と影響線の考え方を用いる。
たわみの影響線と同様に,曲げモーメントも影響線を定義できる。
つまり,単位荷重を点![]() に作用させたときの観測点
に作用させたときの観測点![]() の
曲げモーメント
の
曲げモーメント![]() を曲げモーメントの影響線
と呼ぶ。この曲げモーメントの影響線がわかっていれば,ある任意の
分布外力
を曲げモーメントの影響線
と呼ぶ。この曲げモーメントの影響線がわかっていれば,ある任意の
分布外力![]() が作用したときの観測点の曲げモーメントは,
式(4.61)のたわみの場合と同様に
が作用したときの観測点の曲げモーメントは,
式(4.61)のたわみの場合と同様に
| (4.64) |
となる。これは設計上で非常に重要な関係である。
簡単な例を解いてみよう。図-4.57には
片持ち梁の点Bの曲げモーメントの影響線を示した。求めてみよう。
まず![]() の場合には,点Bより右には何も荷重が載っていないので,
点Bで仮想的に切断したその右の部分のモーメントのつり合いから
の場合には,点Bより右には何も荷重が載っていないので,
点Bで仮想的に切断したその右の部分のモーメントのつり合いから
となる。次に![]() の場合には,同じ部分のモーメントのつり合いは
の場合には,同じ部分のモーメントのつり合いは
と求められる。まとめると
となる。すなわち観測点Bに関する限り,もし外力が
それよりも左側![]() に作用する限り何の影響も受けない。
それに反して,観測点より右側に作用する外力から受ける影響は観測点から
離れれば離れるほど大きくなり,片持ち梁先端で最大になる。
ということは,この観測点を危険にしようと思えばできるだけ
先端に大きな外力を載せればいいことがわかる。
ちなみにせん断力の影響線も
同様に求めることができ,
に作用する限り何の影響も受けない。
それに反して,観測点より右側に作用する外力から受ける影響は観測点から
離れれば離れるほど大きくなり,片持ち梁先端で最大になる。
ということは,この観測点を危険にしようと思えばできるだけ
先端に大きな外力を載せればいいことがわかる。
ちなみにせん断力の影響線も
同様に求めることができ,![]() では
では![]() であり,
であり,![]() では
では
となることから
と求められる。
設計の段階では,外力のパターン![]() が示方書で規定されている
(具体的な値の求め方については節-A.2を参照)ので,
この影響線を用いることによって,着目している断面(設計断面)を
最も危険にするような外力の分布を決定でき,その最も危険な外力に対する
曲げモーメントを最大曲げモーメント
と呼んでいる。
つまり,その載荷位置を
が示方書で規定されている
(具体的な値の求め方については節-A.2を参照)ので,
この影響線を用いることによって,着目している断面(設計断面)を
最も危険にするような外力の分布を決定でき,その最も危険な外力に対する
曲げモーメントを最大曲げモーメント
と呼んでいる。
つまり,その載荷位置を![]() , (
, (![]() , 2,
, 2, ![]() )とすると
)とすると
のような最大値が得られるように載荷位置![]() と
と![]() を探し出し,
それで得られる左辺の値を最大曲げモーメントと呼ぶのである。
このような外力の載せ方を影響線載荷と呼んでいる。
すなわち上の片持ち梁の例では,集中外力の場合なら先端に,
ある幅を持った等分布外力の場合もできるだけ先端付近のみに
載せたときに断面Bは最も不利になり,その曲げモーメントが
最大曲げモーメントである。
ただし一般的に,ある断面には正負の曲げモーメントが生じるので,
式(4.67)の被積分関数中の
を探し出し,
それで得られる左辺の値を最大曲げモーメントと呼ぶのである。
このような外力の載せ方を影響線載荷と呼んでいる。
すなわち上の片持ち梁の例では,集中外力の場合なら先端に,
ある幅を持った等分布外力の場合もできるだけ先端付近のみに
載せたときに断面Bは最も不利になり,その曲げモーメントが
最大曲げモーメントである。
ただし一般的に,ある断面には正負の曲げモーメントが生じるので,
式(4.67)の被積分関数中の![]() に,
正だけの影響線
に,
正だけの影響線![]() 箇所か,負だけの影響線
箇所か,負だけの影響線![]() 箇所のいずれかを
それぞれ用いて求めた正負の最大曲げモーメント
箇所のいずれかを
それぞれ用いて求めた正負の最大曲げモーメント
![]() に対して
安全を確保する必要がある。
同様に,設計したい断面でのせん断力の影響線を
用いれば,最大せん断力
が算定できる。つまり
に対して
安全を確保する必要がある。
同様に,設計したい断面でのせん断力の影響線を
用いれば,最大せん断力
が算定できる。つまり
であるが, この載荷位置は最大曲げモーメントを得る載荷位置とは異なるので注意する。 最大曲げモーメントと最大せん断力の 計算法については節-2.3.4に 詳しく述べたので,参照して欲しい。
例えば曲げに対する設計の場合は,このようにして求められた最大
曲げモーメント![]() を式(4.16)に代入して,
最外縁応力
を式(4.16)に代入して,
最外縁応力
![]() ,
(
,
(
![]() )を
)を
と算定する。例えば正の最大曲げモーメント(
![]() )に対しては,
断面の上端の
)に対しては,
断面の上端の
![]() は負(圧縮)だから
は負(圧縮)だから
| (4.69) |
になるように,曲げ圧縮強度
![]() を用いて断面の設計をすればいいことになる。
同時に,断面の下端の
を用いて断面の設計をすればいいことになる。
同時に,断面の下端の
![]() は正(引張り)だから
は正(引張り)だから
| (4.70) |
を満足するように,曲げ引張り強度
![]() を用いて断面を設計すればいい。
同じ検討を負の最大曲げモーメント(
を用いて断面を設計すればいい。
同じ検討を負の最大曲げモーメント(
![]() :負の最大値)に対して
行うと,今度は下端が圧縮になるので
:負の最大値)に対して
行うと,今度は下端が圧縮になるので
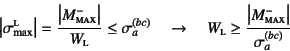 |
(4.71) |
であり,上端の引張り側では
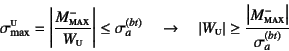 |
(4.72) |
となるので,この4式を満足するように
断面係数![]() と
と![]() を設計することになる。
この二つの強度については,節-7.7.3の
式(7.92) (7.95)を
参照のこと。
最大せん断力に対する設計の考え方は節-2.3.4
(3)の式(2.12)に
述べた通りなので,ここでは説明を省略する。
具体的な計算例については,
トラス(圧縮引張り)については節-2.2.3
(3)を,梁(曲げ)については節-2.3.4
(2)を参照のこと。
を設計することになる。
この二つの強度については,節-7.7.3の
式(7.92) (7.95)を
参照のこと。
最大せん断力に対する設計の考え方は節-2.3.4
(3)の式(2.12)に
述べた通りなので,ここでは説明を省略する。
具体的な計算例については,
トラス(圧縮引張り)については節-2.2.3
(3)を,梁(曲げ)については節-2.3.4
(2)を参照のこと。
となることを示し,例えば幅![]() の等分布外力を作用させる
場合には,どこに配置したときに断面
の等分布外力を作用させる
場合には,どこに配置したときに断面![]() にとって最も危険になるのか
求めよ。それを元に,その断面の
最大曲げモーメントと最大せん断力を求めよ。
にとって最も危険になるのか
求めよ。それを元に,その断面の
最大曲げモーメントと最大せん断力を求めよ。
不静定構造物の影響線は,例えば図-4.58の
問題の解![]() が任意の
が任意の![]() と
と![]() に対して
求められさえすれば,
に対して
求められさえすれば,![]() を代入することに
よって
を代入することに
よって![]() 点の影響線を算定できる。
点の影響線を算定できる。![]() は
たわみの影響線であり
は
たわみの影響線であり
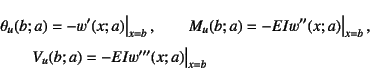
はそれぞれ,たわみ角・曲げモーメント・せん断力の影響線になる。
この影響線を求めるにはもちろん![]() 点に単位荷重を与えた
問題を解けばよく,前節までの解法やあとに述べる近似解法でも
得ることができる。
ここでは値そのものというわけではなく,影響線がどのような
分布になっているのか直感的に知るためにも便利な方法について
概説する。それはMüller-Breslauの定理
と呼ばれている。
物理的な観点からではなく,仮想仕事の原理の有意義な使い方4.9として面白い。
点に単位荷重を与えた
問題を解けばよく,前節までの解法やあとに述べる近似解法でも
得ることができる。
ここでは値そのものというわけではなく,影響線がどのような
分布になっているのか直感的に知るためにも便利な方法について
概説する。それはMüller-Breslauの定理
と呼ばれている。
物理的な観点からではなく,仮想仕事の原理の有意義な使い方4.9として面白い。
たわみの
影響線が,影響線を求めたい点に単位荷重を作用させた
ときのたわみであろうことは,式(4.62)のMaxwellの
相反定理が不静定系でも成立することから簡単に予想できる。
証明は相反定理のそれと同じなので省略する
が,図-4.59のたわみを![]() と
すると,元の問題のたわみの影響線は
と
すると,元の問題のたわみの影響線は
| (4.74) |
として求められる。
たわみ角の
影響線を求めたい場合には,図-4.60の
ように観測点![]() に集中単位外力モーメントを
作用させた場合のたわみ
に集中単位外力モーメントを
作用させた場合のたわみ![]() を考えてみよう。
式(4.56)で示したように集中外力モーメントは
デルタ関数の一階の微係数で表現できた。
したがって,
を考えてみよう。
式(4.56)で示したように集中外力モーメントは
デルタ関数の一階の微係数で表現できた。
したがって,![]() が満足すべきつり合い式は
が満足すべきつり合い式は
となる。この式に![]() を乗じて全領域積分すると
を乗じて全領域積分すると
を得る。ただしここでは,
被積分関数の第1項は4回部分積分をして境界条件を考慮し,
第2項も1回部分積分をしてデルタ関数の定義を用いた。
右辺の被積分関数の中の括弧の中は影響線が満足すべき
つり合い式より![]() でなければならない。
したがってデルタ関数の定義を用いると上式は
でなければならない。
したがってデルタ関数の定義を用いると上式は
| (4.75) |
となる。すなわち,
影響線を計算したい点に単位の集中曲げ外力モーメントを
作用させたときのたわみ形状![]() が,
求めたいたわみ角の影響線
が,
求めたいたわみ角の影響線![]() になる。
になる。
次に
曲げモーメントの影響線
については,観測点にヒンジを挿入して
そこのたわみ角が単位量,つまり1だけ不連続になるように
する問題(4.61)を解いて考えてみよう。
この場合には
となるので,これは
と書いてもいいことは容易に確かめられる。
ということは,図のような1だけたわみ角に不連続がある
場合のたわみはデルタ関数を用いて
という関係があると考えてよさそうである。これをさらに2回
微分するとつり合い式の表現として
を![]() は満足していることになる。上と同様に
この式に
は満足していることになる。上と同様に
この式に![]() を乗じて全領域積分し,部分積分した
あと境界条件を考慮して整理すると
を乗じて全領域積分し,部分積分した
あと境界条件を考慮して整理すると
となるので,結局
| (4.76) |
という関係が求められる。すなわち図-4.61の
ように,観測したい点にヒンジを挿入してたわみ角に1だけの
不連続が発生するようにたわませたときのたわみ形状![]() が,
その点の曲げモーメントの影響線
が,
その点の曲げモーメントの影響線![]() に一致している。
実際にその値を計算するのは面倒ではあるが,
分布の様子は比較的容易に想像できる。
に一致している。
実際にその値を計算するのは面倒ではあるが,
分布の様子は比較的容易に想像できる。
せん断力の
影響線の場合は図-4.62のように,
観測点にスライダーを挿入してその点でたわみが1だけ
不連続になるようにしたときのたわみ形状を求めれば,それが
せん断力の影響線
になる。この場合は
とすればいいので,曲げモーメントの影響線を求める場合と同じように
演算すると
を![]() は満足するから,さらに上と同様の演算をすると
は満足するから,さらに上と同様の演算をすると
となるので
| (4.77) |
ということになり,たわみに不連続がある場合のたわみ形状(の負の値)![]() が
せん断力の影響線分布
が
せん断力の影響線分布![]() になっていることを証明できる。
になっていることを証明できる。
実際に式(4.65) (4.66) (4.73)の 片持ち梁と単純支持梁4.10における 曲げモーメントとせん断力の影響線を 図示したのが図-4.63である。 曲げモーメントは下向きが正,せん断力は上向きが正である。 この図をなんらかの梁のたわみ図であるように捉えた上で 負のたわみ角と負のたわみの点Bでの不連続量を求めると,それぞれ
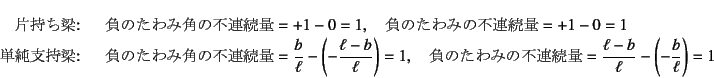
となることから,上式(a) (b)が確かめられる。 つまり,観測断面にヒンジを挿入した上で, そこの負のたわみ角の差が1になるように強制的に変位させた状態の たわみ図が曲げモーメント(下向きが正)の影響線になる。 また,観測断面にスライダーを挿入した上で, そこの負のたわみの差が1になるように強制的に変位させた状態の たわみ図がせん断力(上向きが正)の影響線になる。 同図の一番右に不静定梁の例を示した。
もちろん
この定理を用いなくても,重ね合わせの原理を用いることに
よって影響線を求めることができる。
例として図-4.61の曲げモーメントの影響線を
計算してみよう。
まず右端の支点を取り除いて片持ち梁の静定基本系を考える。
この場合の点![]() の曲げモーメントの影響線
の曲げモーメントの影響線
![]() は
式(4.65)あるいは図-4.57に
示した通りである。
右端に不静定反力
は
式(4.65)あるいは図-4.57に
示した通りである。
右端に不静定反力![]() が作用した系と重ねて元の系に
一致させようとするなら,図-4.64の下の図の
ように,右端に単位荷重が作用したときの点
が作用した系と重ねて元の系に
一致させようとするなら,図-4.64の下の図の
ように,右端に単位荷重が作用したときの点![]() の
曲げモーメントを
の
曲げモーメントを![]() とすることによって,この点
とすることによって,この点![]() の
曲げモーメントの影響線は
の
曲げモーメントの影響線は
と求められるはずである。ただし
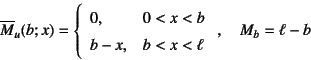
である。
あとは不静定反力![]() を求めればいい。そのためには,
同じく図-4.64の左上の図のように
任意点に単位荷重が載ったときの右端のたわみ
を求めればいい。そのためには,
同じく図-4.64の左上の図のように
任意点に単位荷重が載ったときの右端のたわみ![]() が
求められていれば,それと不静定反力によるたわみを重ね合わせた
たわみが右端で零になる条件から,
その
が
求められていれば,それと不静定反力によるたわみを重ね合わせた
たわみが右端で零になる条件から,
その![]() を求めることができる。つまり
を求めることができる。つまり
ここに![]() は同図下の先端のたわみで,
式(4.37a)から
は同図下の先端のたわみで,
式(4.37a)から
![]() となる。
ところで上の図左の
となる。
ところで上の図左の![]() が
その右の図の
が
その右の図の![]() に等しいことは,Maxwellの相反定理から
明らかである。したがって式(4.36)か
ら
に等しいことは,Maxwellの相反定理から
明らかである。したがって式(4.36)か
ら
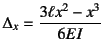 であり,
以上の結果をまとめると結局,曲げモーメントの影響線が
であり,
以上の結果をまとめると結局,曲げモーメントの影響線が
と求められる。