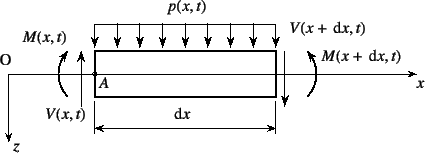
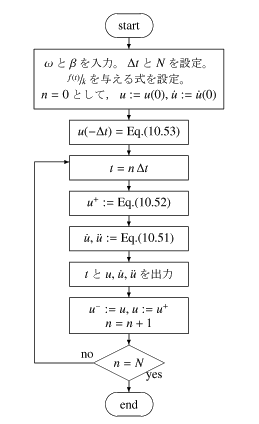
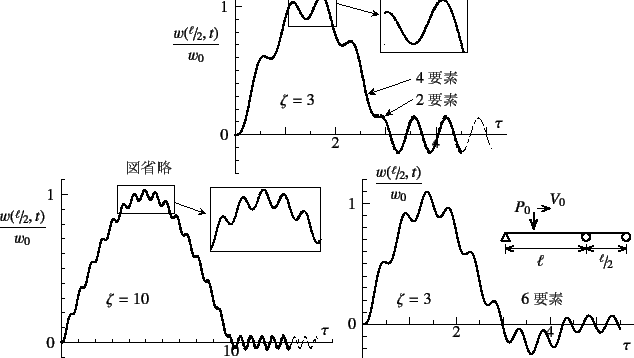
 |
�ŐV�ł𐳊m�ɓǂޏꍇ�ɂ� pdf �t�@�C�� ���ǂ����B����� web �����̂��߂̊ȈՋ��łł��B
�}-10.41�ɂ́C
���z�O��![]() ����p���C�����͂Ƃ��Ă̋Ȃ����[�����g��
����f�͂��������ĉ^�����Ă����Ԃ̗��̔����v�f
����p���C�����͂Ƃ��Ă̋Ȃ����[�����g��
����f�͂��������ĉ^�����Ă����Ԃ̗��̔����v�f![]() ���������B
���̔����v�f��
���������B
���̔����v�f��![]() �����̉^���������́CNewton�̖@������
�����̉^���������́CNewton�̖@������
�ƂȂ�B������![]() ��
��![]() �����̂���݂ł���C
�����̂���݂ł���C![]() ��
���̒P�ʒ���������̎��ʂŁC���x��
��
���̒P�ʒ���������̎��ʂŁC���x��![]() �Ƃ���
�f�ʐς�
�Ƃ���
�f�ʐς�![]() �Ƃ���ƁC
�Ƃ���ƁC![]() �ł���B
���ɓ_A�̔����v���̃��[�����g�̂荇������
�ł���B
���ɓ_A�̔����v���̃��[�����g�̂荇������
��10.11���߂���B
��(10.169)����(10.168)�ɑ�����邱�Ƃ�
����āC�����͂ŕ\�������̉^����������
�ł������Ƃ��킩��B����ɁC![]() �����f�ʂ̐}�S��ʂ�悤�ɒ�`����C
��(4.13b)����
�����f�ʂ̐}�S��ʂ�悤�ɒ�`����C
��(4.13b)����
�Ȃ̂ŁC�������(10.170)�ɑ������C
�ŏI�I�����̉^��������
��
���邢�́C�ȉ��C��l�ޗ����f�ʂ̗�������ΏۂƂ����
�ƂȂ�B�ꏊ![]() �ɂ��Ă̔��W����4�K�ɂȂ��Ă��邪�C
���̂��Ƃƕ����ɖڂ��Ԃ�C
�`���I�ɂ͎�(10.130)�̔g���������ɂ悭���Ă���B
�ɂ��Ă̔��W����4�K�ɂȂ��Ă��邪�C
���̂��Ƃƕ����ɖڂ��Ԃ�C
�`���I�ɂ͎�(10.130)�̔g���������ɂ悭���Ă���B
�����B��ł��邽�߂ɂ́C���E��������(4.28)�̂悤�ɁC
���[![]() ,
, ![]() ,
, ![]() �ɂ����ēK��
�ɂ����ēK��
�Ɨ^�����Ă���K�v������B
������![]() �͔����v���𐳂Ƃ��Ē�`����
����݊p�ł���C
�͔����v���𐳂Ƃ��Ē�`����
����݊p�ł���C![]() �͎�(4.24)��
��`�����f�ʂ̌�����\��������
�͎�(4.24)��
��`�����f�ʂ̌�����\��������
�Ƃ����l�����B
�܂��}-10.42�Ɏ������悤�ɁC![]() ��
��![]() ��
���������̂���f�O�͂Ɣ����v��肪���̊O�̓��[�����g�ł���B
�܂��C���������́C���̏����ʒu�Ə����ŗ^�����������
��
���������̂���f�O�͂Ɣ����v��肪���̊O�̓��[�����g�ł���B
�܂��C���������́C���̏����ʒu�Ə����ŗ^�����������
�Ƃ�������B
�ŏ��͍ł���{�I�Ȏ��R�U���C�܂�
![]() �Œ[�O�͂�
��̏ꍇ�������Ă������B���������̐߂ł́C
�ŗL����p������␔�w�I�ȃA�v���[�`�����Ă���̂ŁC
�����Ȑl�͓ǂݔ���Ă������B
���Ď��R�U�����́C
�U����͂ōł��d�v�ȌŗL�U�����ƌŗL�U�����[�h�����߂�i�K�ɓ�����B
�O�̐�-10.3.2��������l�́C���̗���
�ꍇ�ɂ́C�܂��ŗL�l���
�Œ[�O�͂�
��̏ꍇ�������Ă������B���������̐߂ł́C
�ŗL����p������␔�w�I�ȃA�v���[�`�����Ă���̂ŁC
�����Ȑl�͓ǂݔ���Ă������B
���Ď��R�U�����́C
�U����͂ōł��d�v�ȌŗL�U�����ƌŗL�U�����[�h�����߂�i�K�ɓ�����B
�O�̐�-10.3.2��������l�́C���̗���
�ꍇ�ɂ́C�܂��ŗL�l���
�������������Ƃ��킩�邩������Ȃ����C�����ł͂������C
�܂��ϐ������ʼn����Ă݂悤�B
�������C�ȒP�̂��߂ɁC�ŏ��͒���![]() �̗��[�P���x���̖���
�ΏۂƂ���B
�̗��[�P���x���̖���
�ΏۂƂ���B
�܂��C����݂�ϐ���������
�ƒu���āC�^��������(10.172)�ɑ�����āC�ϐ������Ȃ��琮�������
�̂悤�ɁC���ӉE�ӂ��萔�łȂ���Ȃ�Ȃ����Ƃ��킩��B
�����Ƀv���C����![]() �ɂ������ł���B
���E�����́C���[�ł����
�ɂ������ł���B
���E�����́C���[�ł����![]() �Ƃ���݂�2�K�̔��W��
�Ƃ���݂�2�K�̔��W��![]() ��
��ł�������̂ŁC������ϐ�����������ƁC����
��
��ł�������̂ŁC������ϐ�����������ƁC����
�ƂȂ�B���������͕����ł��Ȃ��̂ŁC�܂�������̂�![]() �̕��ŁC
���̔����������͏㎮����
�̕��ŁC
���̔����������͏㎮����
�ł���B���́C��̕ϐ��������������������̂����C![]() �̕���
����ƁC
�̕���
����ƁC![]() �����łȂ���������^�������Ȃ����Ƃ͖��炩�ł��邪�C
�����ł́C�ŗL�������߂��ʓI�ȃA�v���[�`�𑱂��Ă����B
�����łȂ���������^�������Ȃ����Ƃ͖��炩�ł��邪�C
�����ł́C�ŗL�������߂��ʓI�ȃA�v���[�`�𑱂��Ă����B
�܂�
![]() �̏ꍇ�́C��ʉ���
�̏ꍇ�́C��ʉ���
�ƂȂ�B��������E�����ɑ������ƁC�ŏI�I��
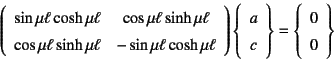
�ƂȂ邪�C���̌W���s��͐����Ȃ̂ŁC![]() ,
, ![]() �͗���������݂��Ȃ��B
�������
�͗���������݂��Ȃ��B
�������![]() �̏ꍇ������������݂��Ȃ����Ƃ͂����ɂ킩��B
�̏ꍇ������������݂��Ȃ����Ƃ͂����ɂ킩��B
����������
![]() �Ƃ����ƁC��ʉ���
�Ƃ����ƁC��ʉ���
�ƂȂ�B��������E�����ɑ�������
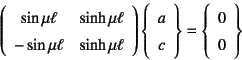
�ɂȂ�B���̏ꍇ�ɂ́C![]() �܂���
�܂���![]() ����ɂȂ�Ȃ���������C
�W���s��͓��قɂȂ�Ȃ���Ȃ�Ȃ��̂ŁC
���̍s�̗�������߂悤�Ƃ����
����ɂȂ�Ȃ���������C
�W���s��͓��قɂȂ�Ȃ���Ȃ�Ȃ��̂ŁC
���̍s�̗�������߂悤�Ƃ����
����C�C�ӂ̐���![]() , 2,
, 2, ![]() �ɑ���
�ɑ���
�ŁC![]() ���s��ɂȂ�̂�
���s��ɂȂ�̂�
�Ƌ��߂���B����![]() ���ŗL�l�ŁC
���ŗL�l�ŁC![]() ���ŗL���C
�܂�ŗL�U�����[�h�ɂȂ�B
���ŗL���C
�܂�ŗL�U�����[�h�ɂȂ�B
����������
�ł��邩��C�e![]() �ɑ���
�ɑ���![]() �ɂ��Ă̔�����������
�ɂ��Ă̔�����������
�ƂȂ�̂ŁC������
�ƒu���C����
�Ƌ��߂邱�Ƃ��ł��C���R�U������
�ƕ\�����Ƃ��ł���B
�܂�C���̐U���́C��(10.175)�̂悤�ɎO�p����
�o�Ȑ����̑g�ݍ��킹�ŕ\�����ŗL�U�����[�h�������C
��(![]() )�̂悤�ȌŗL�U�����ŒP���ɐU�����邱�ƂɂȂ�B
�ŗL�U�����́C1���R�x�n�̂���
)�̂悤�ȌŗL�U�����ŒP���ɐU�����邱�ƂɂȂ�B
�ŗL�U�����́C1���R�x�n�̂���
![]() �Ɠ��l�C
�Ȃ����������ʂŏ��������̂̕�����
�Ɠ��l�C
�Ȃ����������ʂŏ��������̂̕�����
![]() ��
�`����������B
��
�`����������B![]() ,
, ![]() ��������������
���߂���@�ɂ��ẮC��-10.4.4�ŏq�ׂ�B
��������������
���߂���@�ɂ��ẮC��-10.4.4�ŏq�ׂ�B
���������
���������V����I�ȍH�w�I�ȕ��@���q�ׂ悤�B����
�U�����Ȃ̂ŁC���Ԃɂ��Ă͂���U����![]() �ŐU������
���ɂȂ�͖̂��炩��������Ȃ��B���������āC���a�U������
�ŐU������
���ɂȂ�͖̂��炩��������Ȃ��B���������āC���a�U������
�Ɖ��肵�悤�Bp.![]() �ŕϐ�����������[
�ŕϐ�����������[![]() ]����
�U�����ɂȂ�
]����
�U�����ɂȂ�![]() ���ɋ��߂��ƍl��������B
���ɋ��߂��ƍl��������B![]() ���ŗL�U�����[�h
�ɂȂ�B���̎�(10.177)���C
���ŗL�U�����[�h
�ɂȂ�B���̎�(10.177)���C
![]() �Ƃ���
�^��������(10.172)�ɑ�������
�Ƃ���
�^��������(10.172)�ɑ�������
�ƂȂ�B���ꂪ�C�ӂ̎���![]() �Ő������Ȃ���Ȃ�Ȃ��̂ŁC
�Ő������Ȃ���Ȃ�Ȃ��̂ŁC![]() ��
��
�����Ȃ���Ȃ�Ȃ��B������
�ƒ�`����ƁC�㎮(10.178)�̈�ʉ���
�ƂȂ�B����͓��R�C�O�߂ŋ��߂���(10.175)�Ɠ������̂ł���B
�܂����[�P���x������ΏۂƂ��悤�B���E��������(10.177)��
�������C�C�ӂ̎����ɐ������邱�Ƃ���C![]() �݂̂�
�݂̂�
�ƕ\�����B���̏����Ɏ�(10.180)�̈�ʉ����������
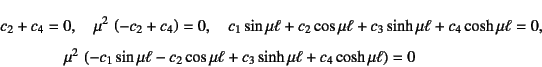
�ƂȂ�̂ŁC�s��\�������
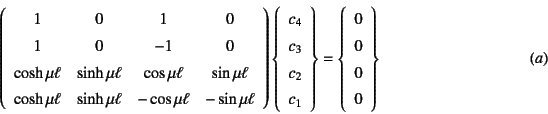
�ƂȂ�B�ϕ��萔���L�ӂȉ��邽�߂ɂ́C���̌W���s���قł�������̂�
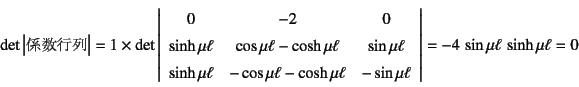
����������������ƂɂȂ�B����������
�ƂȂ�B���̌��ʂ��㎮(![]() )�ɑ������ƁC
)�ɑ������ƁC![]() �݂̂��s��ɂȂ�̂�
�݂̂��s��ɂȂ�̂�
�ł���B����![]() ���ŗL�l�ŁC
���ŗL�l�ŁC![]() ��
�ŗL�U�����[�h�ɂȂ�B��(
��
�ŗL�U�����[�h�ɂȂ�B��(![]() )��
�ŗL�l����(10.179)�ɑ������C�ŗL�U������
)��
�ŗL�l����(10.179)�ɑ������C�ŗL�U������
�ɂȂ�B�ŏI�I�ɉ��́C���ׂẴ��[�h�̏d�ˍ��킹��
�ƕ\�����B���̖���W��![]() ,
, ![]() �͏�����������
���߂Ȃ���Ȃ�Ȃ����C
����ɂ��Ă͐�-10.4.4��
��������B�}-10.43�ɑ�1�`3�����[�h�ƐU����������B
�͏�����������
���߂Ȃ���Ȃ�Ȃ����C
����ɂ��Ă͐�-10.4.4��
��������B�}-10.43�ɑ�1�`3�����[�h�ƐU����������B
���[���Œ肳�ꂽ�Ў������̏ꍇ�ɂ́C���E������
�ɂȂ�B���̏����Ɏ�(10.180)�̈�ʉ����������
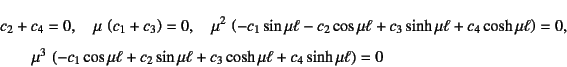
�ƂȂ�̂ŁC�s��\�������
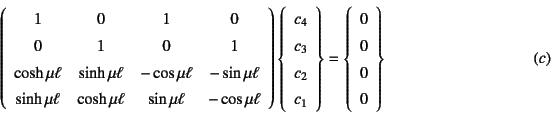
�ƂȂ�B�ϕ��萔���L�ӂȉ��ɂȂ邽�߂ɂ́C
���̌W���s���قł�������̂�
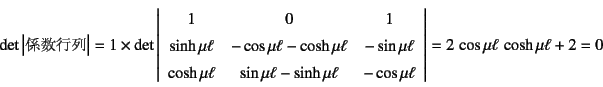
����������������ƂɂȂ�B����������
������![]() (
(![]() , 2,
, 2, ![]() )���ŗL�l�ɂȂ�B
���̌��ʂ��㎮(
)���ŗL�l�ɂȂ�B
���̌��ʂ��㎮(![]() )�ɑ�������
)�ɑ�������
�Ƌ��߂���B���ǁC�U�����[�h��
�ɂȂ�B��(10.184)�͗z�ɉ������Ƃ͂ł��Ȃ��̂ŁC
�Ⴆ��2���@
���Ő��l�I�ɉ��������B
�ŏ��̎O����Ă�����
���炢�ɂȂ�B�}-10.44�ɑΉ�����U�����[�h��`�����B
�O�߂܂ł͈̔͂ł́C�ŗL�U�����[�h�ƌŗL�U���������߂邱�Ƃ͂ł������C
��ʉ������������ɑ�����Đϕ��萔�����߂���C
�����U�����邱�Ƃ͂܂��ł��Ă��Ȃ������B
�����ł́C�����R�x�n�ł��p�������[�h��͖@����ɑ��ėU�����悤�B
�܂��ł��d�v�Ȃ̂͐U�����[�h�̒��𐫂ł���B
��(10.178)�����![]() �����[�h��
�����[�h��
�����Ă���B�����ŁC��![]() �����[�h�����z�ψʂƂ���悤��
���z�d����S�X�p���Ōv�Z�����
�����[�h�����z�ψʂƂ���悤��
���z�d����S�X�p���Ōv�Z�����
����������B��1�������o���C������ϕ����ċ��E�������l�������
�ƂȂ�B���E����������ɂȂ邱�Ƃɂ��ẮC�P���x����Ў������ł�
���炩���낤�B����ȊO���m���߂Ă݂ė~�����B���������āC��̉��z�d������
�ƕ\�����Ƃ��ł���B����Ɠ����v���Z�X���C��![]() �����[�h�̉^����������
��
�����[�h�̉^����������
��![]() �����[�h�Ƃ̉��z�d���̎Z��ōs����
�����[�h�Ƃ̉��z�d���̎Z��ōs����
��B���̓�̎���������������ƁC���ǁC��1���͓����Ȃ̂ŏ����Ă��܂�
�ƂȂ�B�����R�x�n�ł����������悤�ɁC���肵���\���ł���C
�قȂ��̌ŗL�U�����͈قȂ�l�������Ă��邱�Ƃ���C���̎���
�ł��邱�Ƃ������Ă���B
���̎��́C��̊��́i�d��![]() �����j����
���`���Ă���C���̓��ς���ɂȂ邱�Ƃ���C�ŗL�U�����[�h��
���݂����������Ă���
�ƌĂ�ł���B�������[�h���m�̓��ς́C���`�㐔����̗ސ��ŁC
�ŗL�U�����[�h�́u�m�����v�ƍl���Ă��悭�C�����
�����j����
���`���Ă���C���̓��ς���ɂȂ邱�Ƃ���C�ŗL�U�����[�h��
���݂����������Ă���
�ƌĂ�ł���B�������[�h���m�̓��ς́C���`�㐔����̗ސ��ŁC
�ŗL�U�����[�h�́u�m�����v�ƍl���Ă��悭�C�����
�ƋL�����Ƃɂ���B
![]() �́C
�����R�x�n�̂���Ɠ��l��ʉ����ꂽ����
�ƌĂ��B���������āC��(10.187)�ƈꏏ�ɂ����
�́C
�����R�x�n�̂���Ɠ��l��ʉ����ꂽ����
�ƌĂ��B���������āC��(10.187)�ƈꏏ�ɂ����
�Ə������Ƃ��ł���B
���̎�(10.189)��![]() ���C��(10.186)��
�p����
���C��(10.186)��
�p����![]() �Œu���������
�Œu���������
�ƂȂ邱�Ƃ���C��(10.189)�̒��𐫂͕ʂ̓��ς̒�`��p����
�ƒ�`���Ă��������ƂɂȂ�B
���邢�́C���������J�b�R�ǂ����邽�߂ɁC2���ϕ���������ŋ��E������
�l������ƁC���ǁC��̊��̔��W���̊K���������ɂȂ邱�Ƃ���C
������ʂ́u�Ώ̂ȁv�i�d��![]() �����j���ς���`�ł�
�����j���ς���`�ł�
�Ə����Ă������B���z�d���I�ɂ̓J�b�R�������C�ȉ��ł͎g��Ȃ��B
�ł͍ŏI�I�Ɏ��R�U���������߂Ă������B
�O�߂܂łŁC��(10.176)�⎮(10.183)�̂悤�ɁC
�������݂���ŗL�U�����[�h��p���āC����
�Ƌ����\���ł��邱�Ƃ��킩�����B
���̖���W�������肷�邽�߂ɁC����������(10.174)�ɑ�������
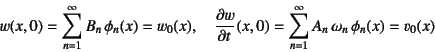
�ƂȂ�B�����Ƃ���U�����[�h![]() �Ƃ��C��(10.189)��
��`�������ς��Ƃ��
�Ƃ��C��(10.189)��
��`�������ς��Ƃ��
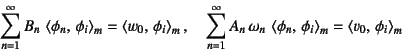
�ƂȂ邪�C���[�h�̒��𐫂��瑍�a�̍��͑�![]() ���ȊO�͗�ɂȂ�
���ȊO�͗�ɂȂ�
�Ƃ����W��B���������āC����W����
�Ƌ��߂��C�B��̉��邱�Ƃ��ł���B
�����C�ޗ����̂��̂ɔS����R������ꍇ�ɂ́C
���̉��͂Ђ��݊W��(4.7)�̋Ȃ��̕����������o����
�Ƃ��������f���͕����I�ɂ͗e�F�ł��������B
������![]() �͍ޗ��̔S���W���ł���B
���������āC������Ȃ����[�����g�̒�`�ɑ������C��(10.171)��
�����
�͍ޗ��̔S���W���ł���B
���������āC������Ȃ����[�����g�̒�`�ɑ������C��(10.171)��
�����
�ƂȂ�B���������āC�^���������́C��(10.172)�̑����
�Ƃ���������ƂɂȂ�B
�܂��C���E��������(10.173)�̑���ɁC���̂悤�ɂȂ�B
�ł͎��R�U���̏ꍇ(
![]() )�ɁC����
)�ɁC����
�̋����\���ŕ\�������̂Ƃ��āC���[�h��͂����悤�B
������![]() �́C���̌ŗL�U�����[�h�ł��邱�Ƃ�
���ӂ���B
�́C���̌ŗL�U�����[�h�ł��邱�Ƃ�
���ӂ���B![]() �͗�����ʉ����ꂽ���W
�ł���B���̎����C�^��������(10.196)�ɑ�������
�͗�����ʉ����ꂽ���W
�ł���B���̎����C�^��������(10.196)�ɑ�������
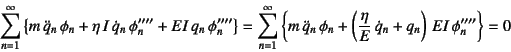
�ƂȂ�B���̉^���������Ƒ�![]() �����[�h�Ƃ̓��ς��Ƃ邽�߂�
�����[�h�Ƃ̓��ς��Ƃ邽�߂�
�Ƃ�����p�𗼕ӂɂ���ƁC
���ǁC��(10.189) (10.190)�̒���������p���邱�Ƃɂ���āC
���a�̑�![]() ���݂̂����o�ł��C���ꂪ
���݂̂����o�ł��C���ꂪ
�Ƃ����C1���R�x�n�̔S���������R�U���̌`�̉^���������ɂȂ�B����
��2���̌W�����`���I�ɁC��(10.18)��1���R�x�n�̌�������
�W��
![]() �̕\����
�u���������̂ŁCBernoulli-Euler������ʉ����ꂽ�����萔
��
�̕\����
�u���������̂ŁCBernoulli-Euler������ʉ����ꂽ�����萔
��
�ƒ�`�ł���B���傤�ǁC��(10.120)�Œ�`����Rayleigh������
�����̍������̌����萔
![]() ��
���������������ƂɂȂ�B
���������āC��ʉ����ꂽ���W�ŕ\�����^����������
��
���������������ƂɂȂ�B
���������āC��ʉ����ꂽ���W�ŕ\�����^����������
�ƂȂ�B�`���I�ɂ�1���R�x�n�̌������R�U���̉^���������Ɉ�v����B �������ۂɂ́C�L���v�f�@��p������ŁC ��(10.119)��Rayleigh������p���ĉ�͂���̂����ʂ��Ǝv����B
�S���������l���ł��邱�Ƃ͑O�߂Ŏ��������C�O�߂̂悤�Ȉ����́C
����ł͈�ʓI�ł͂Ȃ���������Ȃ��̂ŁC���炭�͖������C
���̋����U����_���Ă����B
���������āC�^���������͎�(10.172)��
�ł���B����ɁC���R�U�����[�h�ŋ����\��������(10.198)��
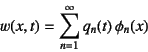
�ʼn����\����邱�Ƃɂ��āC�����U�������������B������![]() ��
���R�U���̐U�����[�h�ł��邱�Ƃɂ͒��ӂ���B�㎮�����̏�̉^����������
��������
��
���R�U���̐U�����[�h�ł��邱�Ƃɂ͒��ӂ���B�㎮�����̏�̉^����������
��������
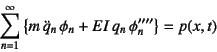
�ƂȂ�B���̉^���������Ƒ�![]() �����[�h�Ƃ̓��ς��Ƃ邽�߂�
�����[�h�Ƃ̓��ς��Ƃ邽�߂�
�Ƃ�����p�𗼕ӂɂ����
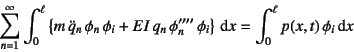
�ƂȂ�B����ɁC��(10.189) (10.190)�̒���������
�p���邱�Ƃɂ���āC���a�̑�![]() �����݂̂𒊏o�ł�
�����݂̂𒊏o�ł�
�ƂȂ�B������
![]() ��
��
�Ⴆ�C1���R�x�n�̎�(10.48)�̒P�ʏՌ������𗘗p�����C
��(10.49)��Duhamel�ϕ���p���ċ����U������
���߂Ă݂�ƁC��̎�(10.201)�̉���
�ƂȂ�̂ŁC�ŏI�I�ɂ���݂�
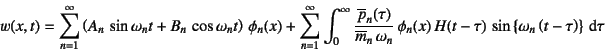
�ƂȂ�B����ɁC��ʉ����ꂽ�O�͂̎�(10.202)�������
��������
�ƕ\���ł���BDuhamel�ϕ����͗돉�������̉�������C
����W��![]() ,
, ![]() �͎�(10.193)�Ɠ����ł���B
�͎�(10.193)�Ɠ����ł���B
�}-10.45�ɂ́C�P�����̍�����1/4�̈ʒu�Ɏ���![]() �Ɉ���
�W���O��
�Ɉ���
�W���O��![]() ���ڂ��C���̂܂܂ɂ����Ƃ��̃X�p�������̉����ƁC
��������\�I�Ȏ����̂���`����������B�O�͂�
���ڂ��C���̂܂܂ɂ����Ƃ��̃X�p�������̉����ƁC
��������\�I�Ȏ����̂���`����������B�O�͂�
������C��(10.203)��Duhamel�ϕ���![]() �ɂ��Ă̐ϕ������ɂ��Ă�
�ɂ��Ă̐ϕ������ɂ��Ă�
�ƂȂ�B���Ƃ̌v�Z�͊ȒP�Ȃ̂ŏȗ�����B
�Ȃ��}����![]() �Əc����
�Əc����![]() ��
��
�ƒ�`�����B![]() �͐ÓI��
�͐ÓI��![]() ���ڂ����Ƃ��̒����̂���݂ł���B
���̐}�̉�����1�����͂ق�0.65���x�Ɍ�����B����C����������
���ڂ����Ƃ��̒����̂���݂ł���B
���̐}�̉�����1�����͂ق�0.65���x�Ɍ�����B����C����������![]() ��
�Z�肵���Ƃ���1��(
��
�Z�肵���Ƃ���1��(![]() )�̌ŗL�U������
)�̌ŗL�U������![]() �Ȃ̂ŁC
����ɑΉ�����1���̌ŗL������
�Ȃ̂ŁC
����ɑΉ�����1���̌ŗL������
![]() �ł���B
���̂��Ƃ���C�ÓI�ȕψʂ𒆐S�ɂ��āC�قƂ��1���U������
�U�����Ă��邾���ł��邪�C�O�͂̈ʒu�����Ă��邽�߁C
����`���1�����[�h�����Ƃ͌���Ȃ����Ƃ������Ă���B
�ł���B
���̂��Ƃ���C�ÓI�ȕψʂ𒆐S�ɂ��āC�قƂ��1���U������
�U�����Ă��邾���ł��邪�C�O�͂̈ʒu�����Ă��邽�߁C
����`���1�����[�h�����Ƃ͌���Ȃ����Ƃ������Ă���B
���āC��(10.203)��
�Ƃ����`�ŕ\�����Ă݂�B������
�ƒu�����B��(10.205)�̉E�ӂ̍Ō�̍��́C�u�ꏊ![]() ��
����
��
����![]() �ɍ�p�����O��
�ɍ�p�����O��![]() �̉e����
�̉e����![]() �{����
�����Z����C���ꂪ�O�͂��ׂĂ̍v���ɂȂ�v�Ƃ����悤�ɂ�
�ǂ߂Ȃ����낤���B���������Ȃ�C��(10.206)��
��`����
�{����
�����Z����C���ꂪ�O�͂��ׂĂ̍v���ɂȂ�v�Ƃ����悤�ɂ�
�ǂ߂Ȃ����낤���B���������Ȃ�C��(10.206)��
��`����![]() �́C���̉e���̓x������\���e�����q�ł���C
���邢�́C�ꏊ
�́C���̉e���̓x������\���e�����q�ł���C
���邢�́C�ꏊ![]() �Ɏ���
�Ɏ���![]() �ɉ����P�ʂ̏Ռ�����p����
�ꍇ�̉����ł���Ƃ͓ǂ߂Ȃ����낤���B
�܂�C
�ɉ����P�ʂ̏Ռ�����p����
�ꍇ�̉����ł���Ƃ͓ǂ߂Ȃ����낤���B
�܂�C
![]() �͗��́u�P�ʏՌ������v�ł�
�Ȃ����ƍl������B�����āC��(10.205)�̊O�͂Ɋւ��鍀�́C
�O�͂̍v������ϕ��\�������C����Duhamel�ϕ�
���낤�B
�����ł́C��(10.206)���{���ɒP�ʏՌ��������ǂ�����
�m�F���������B
�͗��́u�P�ʏՌ������v�ł�
�Ȃ����ƍl������B�����āC��(10.205)�̊O�͂Ɋւ��鍀�́C
�O�͂̍v������ϕ��\�������C����Duhamel�ϕ�
���낤�B
�����ł́C��(10.206)���{���ɒP�ʏՌ��������ǂ�����
�m�F���������B
���̂���ʒu![]() �ɁC����
�ɁC����![]() �ɒP�ʏՌ��O�͂�
��p�����Ƃ���ƁC����͐}-10.46�̂悤��
�ɂȂ�B�����ł́C1���R�x�n�̒P�ʏՌ��������l�����ۂ�
��������Dirac�̃f���^���ŊO�͂��\�����Ƃ��ł��邱�Ƃ𗘗p���Ă���B
�ȒP�̂��߂ɗ��[�P���x������ΏۂƂ���B
�܂��C��-4.4.1�Ő��������悤�ɁC
�W���O�͂�������Dirac�̃f���^���ŕ\�����Ƃ��ł��邱�Ƃ���C
���̐}�̂悤�ȒP�ʏՌ��O�͂�
�ɒP�ʏՌ��O�͂�
��p�����Ƃ���ƁC����͐}-10.46�̂悤��
�ɂȂ�B�����ł́C1���R�x�n�̒P�ʏՌ��������l�����ۂ�
��������Dirac�̃f���^���ŊO�͂��\�����Ƃ��ł��邱�Ƃ𗘗p���Ă���B
�ȒP�̂��߂ɗ��[�P���x������ΏۂƂ���B
�܂��C��-4.4.1�Ő��������悤�ɁC
�W���O�͂�������Dirac�̃f���^���ŕ\�����Ƃ��ł��邱�Ƃ���C
���̐}�̂悤�ȒP�ʏՌ��O�͂�
�ƕ\���ł��邱�Ƃ��킩��B
���̂悤�ȊO�͂ɑ���P�ʏՌ�������
![]() ��
�L�����Ƃɂ���ƁC���̉^����������
��
�L�����Ƃɂ���ƁC���̉^����������
�ƕ\�����B�܂����E������
�ł���C���������͗돉�������Ƃ���B�������CFourier�ϊ����g���̂ŁC
���������͊g�����āC����![]() �ɐÎ~���Ă������̂Ƃ���
�^��������̂Ƃ���B
�ɐÎ~���Ă������̂Ƃ���
�^��������̂Ƃ���B
�܂��C���̒P�ʏՌ�������Fourier�ϊ��������̂�
�ƋL�����Ƃɂ���B���ɉ^����������Fourier�ϊ����悤�B
�܂����ӑ�1����Fourier�ϊ��́C�����ϕ���2���
�ƂȂ�̂ŁC���������Ǝ�(![]() )���������
)���������
�ƂȂ�B
�ŏI�I��Fourier�t�ϊ��̐ϕ�������ۂɂ́C���f�ϕ����g���K�v��
����̂ŁC����![]() �����f���Ɋg������
�����f���Ɋg������
![]() ��
����ƁC
��
����ƁC
![]() �ƂȂ�̂ŁC
�㎮��1����
�ƂȂ�̂ŁC
�㎮��1����![]() �̍����ɂ��邽�߂ɂ�
�̍����ɂ��邽�߂ɂ�
�Ƃ��������C�܂�C![]() �̋�����
�̋�����![]() ��
���ł���K�v������B���̏������ő�1����Fourier�ϊ���
��
���ł���K�v������B���̏������ő�1����Fourier�ϊ���
�ɂȂ�B���ɍ��ӑ�2����Fourier�ϊ��́C������Fourier�ϊ���
���Ԃ����ւ��邾���Ȃ̂ŁC��(![]() )��������
)��������
�ƂȂ�B�Ō�ɉE�ӂ�Fourier�ϊ��́CDirac�̃f���^���̒�`����
�ƂȂ�B���������āC���̎�(![]() ) (
) (![]() ) (
) (![]() )���^����������
�`�ɑg�݂Ȃ�����
)���^����������
�`�ɑg�݂Ȃ�����
�ƂȂ�B���E������(![]() )�����l��Fourier�ϊ����Ă��܂��ƁC
����
)�����l��Fourier�ϊ����Ă��܂��ƁC
����![]() ��
��
�̔��������������C���E������
�ŗ^������B
��������[�h��͖@�ʼn������Ƃɂ��C![]() ����(10.181)��
�ŗL�U�����[�h�̋������Ƃ���
����(10.181)��
�ŗL�U�����[�h�̋������Ƃ���

�Ɖ��肷��B�������(![]() )�ɑ�������
)�ɑ�������
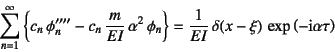
�ƂȂ�B�v���C����![]() �ɂ������ł���B
���̍��ӑ�1���Ɏ�(10.186)���������
�ɂ������ł���B
���̍��ӑ�1���Ɏ�(10.186)���������
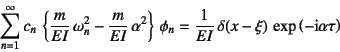
���邢��
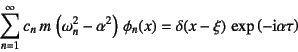
�ƂȂ�B�����![]() �Ƃ̓��ς��Ƃ邽�߂ɁC���ӂ�
�Ƃ̓��ς��Ƃ邽�߂ɁC���ӂ�
�Ƃ�����p�����C��(10.189)�̒���������
�p����C���a�̑�![]() �����݂̂𒊏o�ł�
�����݂̂𒊏o�ł�
�ƂȂ�B�E�ӂ̉��Z�ł�Dirac�̃f���^���̒�`���g�����B����������
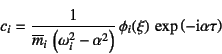
�Ƌ��߂���B�������(![]() )�ɖ߂����Ƃɂ����
)�ɖ߂����Ƃɂ����
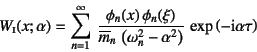
��B1���R�x�n�̎�(10.55)�̎��g���������̌`��C
��(10.60)�Ɏ������P�ʏՌ������Ǝ��g���������̊W����C
����![]() �́C�������g���������Ɂu�����v���邱�Ƃ��킩��B
�́C�������g���������Ɂu�����v���邱�Ƃ��킩��B
����ŁC�P�ʏՌ�������Fourier�ϊ������߂�ꂽ����C
������t�ϊ�����Ή��邱�Ƃ��ł���B�܂�
�ł��邩��C����ɏ㎮���������
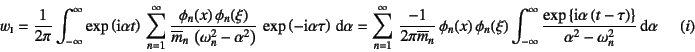
�ƂȂ�B���̉E�ӂ̍Ō�̐ϕ�
�����߂���C�P�ʏՌ����������߂邱�Ƃ��ł���B
���̐ϕ�![]() �́C
�́C![]() �f���Ƒ��������f�ϕ��ŋ��߂���B
���ꂪ
�f���Ƒ��������f�ϕ��ŋ��߂���B
���ꂪ
![]() �ŗ�ɂȂ�C���f���ʏ�̂�����1�ʂ���
�ł���B�܂���(
�ŗ�ɂȂ�C���f���ʏ�̂�����1�ʂ���
�ł���B�܂���(![]() )�̏�������C
�ϕ��o�H�͎����̎���i
)�̏�������C
�ϕ��o�H�͎����̎���i![]() �̋����������łȂ���Ȃ�Ȃ�����j��
�ʂ邱�Ƃɒ��ӂ���K�v������B�܂�}-10.47(a)��
������
�̋����������łȂ���Ȃ�Ȃ�����j��
�ʂ邱�Ƃɒ��ӂ���K�v������B�܂�}-10.47(a)��
������![]() �̌o�H���C
�̌o�H���C![]() ����
����![]() �܂�
���ϕ�����
�܂�
���ϕ�����
![]() ��
��![]() ��
�l�ɂȂ�B
��
�l�ɂȂ�B![]() �͕��f���Ȃ̂�
�͕��f���Ȃ̂�
![]() ��
����ƁC
��
����ƁC
![]() �ƂȂ�B
���������āC���̐ϕ��f���ʂ�1���ϕ�����ꍇ�C
�������_�ł�
�ƂȂ�B
���������āC���̐ϕ��f���ʂ�1���ϕ�����ꍇ�C
�������_�ł�![]() ���l�@�����
���l�@�����
�����҂ł���B
�����҂ł���B
������C![]() �̂Ƃ��͎��ϕ�(
�̂Ƃ��͎��ϕ�(
![]() )��
�̈���ɋɂ͑��݂����C
)��
�̈���ɋɂ͑��݂����C![]() �͐������ł��邩��CCauchy�̐ϕ��藝
���
�͐������ł��邩��CCauchy�̐ϕ��藝
���
�ƂȂ�̂ŁC��(![]() )���l������ƁC����
)���l������ƁC����
�Ƌ��߂���B
�܂�![]() �ł���C��(10.206)�ƈ�v����B
�ł���C��(10.206)�ƈ�v����B
�t��![]() �̂Ƃ��͎��ϕ�(
�̂Ƃ��͎��ϕ�(
![]() )��
�̈���ɋɂ���ӏ����邱�Ƃ���C����ϕ��͗���
�̒藝��
)��
�̈���ɋɂ���ӏ����邱�Ƃ���C����ϕ��͗���
�̒藝��
�̂悤�ɋ��߂邱�Ƃ��ł���B
������
![]() �́C
�́C![]() ��
�������
��
�������![]() �̗�����\���Ă���B���������āC�㎮(
�̗�����\���Ă���B���������āC�㎮(![]() )���l�������
)���l�������
�ƂȂ�B1�ʂ̋ɂ̗�����
�Ƌ��߂���B
���������āC
![]() �Ƃ��āCEuler��
����(10.62)��p�����
�Ƃ��āCEuler��
����(10.62)��p�����
�����߂��������ϕ��l�ɂȂ�B
�������(![]() )�ɑ�����āC
)�ɑ�����āC![]() �̒P�ʏՌ�������
�̒P�ʏՌ�������
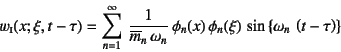
�ƕ\�����Ƃ��ł���B����͎�(10.206)�Ɉ�v����B
�����ł͔S��������ꍇ�̒莮�������Ă����B
�^���������͎�(10.196)�ł���C
���E�����͎�(10.197)�ŗ^������B
�����ł͊ȒP�̂��߂ɗ��[�P���x������ΏۂƂ���B
���������͗돉�������ł���B����C
�P�ʏՌ�����
![]() ��
�������E�����E����������
��
�������E�����E����������
�ŕ\�����^�������������Ă���B
����ɑ��C��-10.1.3 (5)��
�p�����悤�Ȑ������
���l����K�v������C�����
![]() ��
��
�ŕ\�����^��������������B���Ȑ����n�ł͂Ȃ����Ƃ���C
�������͏㎮�̌��̖��̌�������
�������قȂ邱�Ƃɉ����āC���������ł͂Ȃ��C![]() ��
�I��������������Ƃ���
��
�I��������������Ƃ���
�Ɨ^������悤�ȏI�ǒl���Ƃ��Ē�`�����B���E������
�������̕�����ς��Ȃ���Ȃ�Ȃ�(
![]() )���Ƃɒ��ӂ���B
)���Ƃɒ��ӂ���B
�ŏ��Ɍ��̖��Ɛ������̒P�ʏՌ�����![]() �Ƃ̓��ς��Ƃ��
�Ƃ̓��ς��Ƃ��
�ł��邪�C�܂����ӂ̊�������
�ƂȂ�B�����ł́C![]() �̗돉�������Ǝ�(
�̗돉�������Ǝ�(![]() )�̗�I��������p�����B
�^���������̔S�����ƍ������͂܂�
)�̗�I��������p�����B
�^���������̔S�����ƍ������͂܂�![]() ��2���ϕ����āC
���[�̋��E�������l�������
��2���ϕ����āC
���[�̋��E�������l�������
![\begin{eqnarray*}
&& \int_0^\ell w^*\subsc{i}\left(
\eta I\D[5][4][x]{w}{t}
+E...
...{x}\left(
\eta I\D[3][2][x]{w}{t}
+EI\D[2]{w}{x}\right)\dint x
\end{eqnarray*}](s4img1069.gif)
�ƕ\�����Ƃ��ł���̂ŁC��U��
�ƂȂ�B���̑�1�������ԕ�����1���ϕ������
�Ə���������B
�����ł�![]() �̗돉����������
�̗돉����������
![$\D[2]{w}{x}(x,0)=0$](s4img1072.gif) �Ƃ��C
�Ƃ��C![]() ��
��I����������
��
��I����������
![$\D[2]{w^*\subsc{i}}{x}=0$](s4img1073.gif) ����������Ƃ����B
���������āC�S���ƍ����̍���
����������Ƃ����B
���������āC�S���ƍ����̍���
�ƂȂ�B�ēx![]() �ɂ���2���ϕ����ċ��E�������l�������
�ɂ���2���ϕ����ċ��E�������l�������
![\begin{eqnarray*}
&& \int_0^\ell \D[2]{w}{x}\left(
-\eta I\D[3][2][x]{w^*\subsc...
...[4][x]{w^*\subsc{i}}{t}
+EI\D[4]{w^*\subsc{i}}{x}\right)\dint x
\end{eqnarray*}](s4img1075.gif)
�ƂȂ�B���̌��ʂƊ��������ꏏ�ɂ܂Ƃ߂�ƁC�ŏI�I��
�ƕ\���ł���̂ŁC��(![]() )�����ӂ̒����ʂɑ�������
)�����ӂ̒����ʂɑ�������
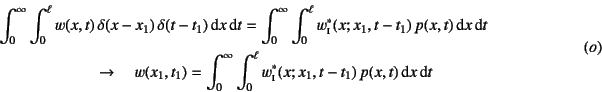
�Ƃ����W�����藧�B
�S�������v���Z�X���C�P�ʏՌ����̎�(![]() )��
�������̒P�ʏՌ�����
)��
�������̒P�ʏՌ�����![]() �Ƃ̓��ςɑ��Ď��s�����
�Ƃ̓��ςɑ��Ď��s�����
�ƂȂ�̂ŁC���ӂ̒����ʂɎ�(![]() )���������
)���������
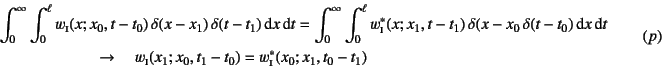
�Ƃ����W��B
�܂������藝
���B
���̎�(![]() )����(
)����(![]() )��
������邱�Ƃɂ����
)��
������邱�Ƃɂ����
�Ƃ���Duhamel�ϕ��̕\����B
����͎�(10.205)�̉E�ӑ�2���Ɉ�v����B
��(10.199)�̔S�������萔��p���āC1���R�x�n��
�P�ʏՌ������̉��̎�(10.47)���Q�l�ɂ���ƁC
�������܂��̒P�ʏՌ�������
�ɂȂ�B������
�ƒ�`�����B
��Ƃ��āC���̑��x![]() ��
��![]() �̐������ɑ����֎ԁi�W���O�́j
�̐������ɑ����֎ԁi�W���O�́j![]() �ɂ��
�P���x�����̔��U������͂��Ă݂悤�B��֎Ԃ����̍��[�ɍڂ����u�Ԃ�
����
�ɂ��
�P���x�����̔��U������͂��Ă݂悤�B��֎Ԃ����̍��[�ɍڂ����u�Ԃ�
����![]() �Ƃ���ƁC�}-10.48�Ɏ������悤�ɁC
�Ƃ���ƁC�}-10.48�Ɏ������悤�ɁC![]() �b��ɂ�
��֎Ԃ�
�b��ɂ�
��֎Ԃ�![]() �̈ʒu�ɂ���̂ŁC���̊O�͂�
�̈ʒu�ɂ���̂ŁC���̊O�͂�
�ƕ\�����Ƃ��ł���B![]() �͒P�ʒ���������̕��z�O�͂Ƃ��ĕ\����
�W���O�́i�͐ς̂悤�Ȃ��́j�Ȃ̂ŁC�͂̒P�ʂ������Ƃɒ��ӂ���B
�͒P�ʒ���������̕��z�O�͂Ƃ��ĕ\����
�W���O�́i�͐ς̂悤�Ȃ��́j�Ȃ̂ŁC�͂̒P�ʂ������Ƃɒ��ӂ���B
�����Duhamel�ϕ��̎�(10.207)��
��������
�ɂȂ�B�O�͂̕ϐ���![]() ��
��![]() �ɂȂ��Ă��邱�Ƃɒ��ӂ���B
����Ɏ�(10.208)�̒P�ʏՌ�������
�����萔��
�ɂȂ��Ă��邱�Ƃɒ��ӂ���B
����Ɏ�(10.208)�̒P�ʏՌ�������
�����萔��
![]() �Ƃ������̂������C
�P���x�����̌ŗL�U�����[�h�̎�(10.181)��
�������ƁC
�Ƃ������̂������C
�P���x�����̌ŗL�U�����[�h�̎�(10.181)��
�������ƁC
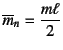 �Ȃ̂�
�Ȃ̂�
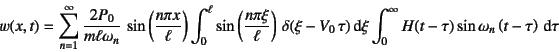
�ƂȂ�B![]() �ɂ��Ă̐ϕ��������o���ƁCDirac�̃f���^����
��`�ɂ���āC���̍��͐ϕ��͈͓���
�ɂ��Ă̐ϕ��������o���ƁCDirac�̃f���^����
��`�ɂ���āC���̍��͐ϕ��͈͓���![]() ������Ƃ��C
�܂�
������Ƃ��C
�܂�
![]() �̂Ƃ��ɂ����l���������C����ȊO�ł͗��
�Ȃ邱�Ƃ��킩��B�܂�C
�̂Ƃ��ɂ����l���������C����ȊO�ł͗��
�Ȃ邱�Ƃ��킩��B�܂�C
![]() �̂Ƃ������l��
�����Ƃ��ł���̂�
�̂Ƃ������l��
�����Ƃ��ł���̂�
�ƂȂ�B����͓�����O���낤�B�Ƃ����̂�
![]() �́C
��֎Ԃ����̊O�ɏo�鎞��������ł���B������
�́C
��֎Ԃ����̊O�ɏo�鎞��������ł���B������
�ƒu���ƁC��̉���
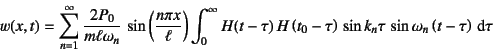
�Ə������Ƃ��ł���B���Heaviside�������
�͈̔͂Őϕ�����������Ƃ������Ă���B���������ď㎮��
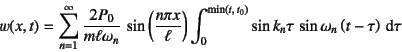
���v�Z����������ƂɂȂ�B![]() ��
��![]() ��
��![]() ��
���������Ƃ���
��
���������Ƃ���
�̐ϕ����ł�����������ł��邪�C
�璷�ɂȂ�̂ŁC���̌v�Z�͏ȗ����Č��ʂ�����������
�ƂȂ�B
�܂�C��֎Ԃ��ڂ��Ă���Ԃ͌ŗL�U����![]() ��
�O�͂̉^���ɋN������U����
��
�O�͂̉^���ɋN������U����![]() �Ƃ�
�����̓����œ����Ă��邪�C�ʉ߂������Ƃ͌ŗL�U����������
���R�U������B�}-10.49�ɂ́C����
��\�I��3�_�̉������������B
���̐}�͋���10����p�������ʂł��邪�C100���ł���ʂ͂��Ȃ��B
�܂��}�ŗp�����L���́C��(10.204)�Œ�`����
�Ƃ�
�����̓����œ����Ă��邪�C�ʉ߂������Ƃ͌ŗL�U����������
���R�U������B�}-10.49�ɂ́C����
��\�I��3�_�̉������������B
���̐}�͋���10����p�������ʂł��邪�C100���ł���ʂ͂��Ȃ��B
�܂��}�ŗp�����L���́C��(10.204)�Œ�`����![]() �̑��ɂ�
�̑��ɂ�
�ƒ�`�����B![]() �̓X�p�������ɏW���O��
�̓X�p�������ɏW���O��![]() ����p�����Ƃ���
�����̂���݂ł���B�܂��C
����p�����Ƃ���
�����̂���݂ł���B�܂��C![]() �Ɉ�֎Ԃ͗�����O�ɏo��B
�����ł́C���Ȃ葬���ʉ߂���ꍇ��
�Ɉ�֎Ԃ͗�����O�ɏo��B
�����ł́C���Ȃ葬���ʉ߂���ꍇ��![]() �Ƃ��C
�������ʉ߂���ʏ�̋������̏ꍇ��
�Ƃ��C
�������ʉ߂���ʏ�̋������̏ꍇ��![]() �Ƃ����B
�ǂ����
�Ƃ����B
�ǂ����![]() �ȍ~�͎��R�U�������Ă���B
���͂��̎�(10.211)�̉��͂ƂĂ��ʔ������ۂ��������Ă���B
����́C���s���x�ɂ���Ă͕�����ɂ���\�������邩��ł���B
�܂�
�ȍ~�͎��R�U�������Ă���B
���͂��̎�(10.211)�̉��͂ƂĂ��ʔ������ۂ��������Ă���B
����́C���s���x�ɂ���Ă͕�����ɂ���\�������邩��ł���B
�܂�![]() �̂Ƃ��C���̉��̐U���͖�����ɂȂ�B
�Ⴆ�C
�̂Ƃ��C���̉��̐U���͖�����ɂȂ�B
�Ⴆ�C![]() �̂Ƃ��ɂ͎�(10.210)����
�̂Ƃ��ɂ͎�(10.210)����
�ƂȂ邩��C
�܂�C��֎Ԃ�����ʉ߂���̂ɕK�v�Ȏ��Ԃ��C����1����
�ŗL�����̔����̂Ƃ��C���͔��U���ɂȂ邱�Ƃ������Ă���B
�����Zimmermann����
�ƌĂԁB�������C�����I�Ȗ��̐ݒ���l����ƁC�����
���I�Ȃ��炢�������x�ň�֎Ԃ��ړ�����ꍇ�ɑ�������B
�Ⴆ�C�����a�ɓS��n���C������V�������炢�̍����ԗ���
�ʉ߂���ꍇ�ł��낤�B���ۂ�
![]() ��
����}-10.50�Ɏ������B�����Ƃ����Ԃ�
�ʉ߂������ƁC�ÓI����ݒ��x�̐U���̎��R�U���ɂȂ�B
����[87]�ɂ��C�U����������ɂȂ�O�Ɉ�֎Ԃ��ʉ߂���̂ŁC
���ۂɂ͐U����������ɂȂ邱�Ƃ͂Ȃ��Ɛ�������Ă���E�E�E���C�ʔ����B
��
����}-10.50�Ɏ������B�����Ƃ����Ԃ�
�ʉ߂������ƁC�ÓI����ݒ��x�̐U���̎��R�U���ɂȂ�B
����[87]�ɂ��C�U����������ɂȂ�O�Ɉ�֎Ԃ��ʉ߂���̂ŁC
���ۂɂ͐U����������ɂȂ邱�Ƃ͂Ȃ��Ɛ�������Ă���E�E�E���C�ʔ����B
�Ƃ��Ă݂��BHeaviside����Dirac�̃f���^���̎g�����̗��K���Ƃ��āC
��������߂Ă݂�B
���ʂ͂��܂�ʔ������̂ł͂Ȃ��C��֎Ԃ̌��ʂ�![]() �����ړ����������炢��
���̂ł���B
�����ړ����������炢��
���̂ł���B
���ۂɕ��G�ȎЉ��Ս\���̐v���̐U����͂� �Δ����������ڗp���邱�Ƃ́C ���f�����̓_���������������ϓ_���������������B ���������āC�����I�ȕ��@�͐��l�I�ɋߎ��I�ɉ������@�ł��낤�B ���̂��߂ɂ́C��(10.196)�̉^���������� ��(10.197)�̋��E�������C���炩�̕��@�ŗ��U�����Ă��� �K�v������B��̑�\�I�Ȏ�@�͗L���v�f�@�̓K�p�ł���B �����ł͗���ΏۂƂ��āC���̗v�f�̒莮���Ɖ�͗�������B
�܂��C����![]() ��1�v�f��ΏۂƂ��C��(10.196)��
�Ή����鉼�z�d���������߂��
��1�v�f��ΏۂƂ��C��(10.196)��
�Ή����鉼�z�d���������߂��
�ƂȂ�B��ϕ����̑�2, 3����2���ϕ�����ƁC�㎮��
![\begin{eqnarray*}
&&\int_0^\ell \left\{ \delta w
m\D[2]{w}{t}+\delta \D[2]{w}{...
...D[3][2][x]{w}{t}
+EI \D[2]{w}{x} \right)\right\vert _0^\ell = 0
\end{eqnarray*}](s4img1120.gif)
�ƂȂ�B�����ł́C����݊p![]() ����(10.173)�ŁC
�����v���𐳂ɒ�`����Ă������Ƃ��l�����Ă���B
���̎��Ɏ�(10.197)�̋��E������������ƁC
�ŏI�I�ɉ��z�d������
����(10.173)�ŁC
�����v���𐳂ɒ�`����Ă������Ƃ��l�����Ă���B
���̎��Ɏ�(10.197)�̋��E������������ƁC
�ŏI�I�ɉ��z�d������
�ƕ\�����B�����ɁC![]() ,
, ![]() �͍��[
�͍��[![]() �̂���݂�
����݊p�ł���C
�̂���݂�
����݊p�ł���C![]() ,
, ![]() �͉E�[
�͉E�[![]() �̊e�ʂł���B
�܂��C
�̊e�ʂł���B
�܂��C![]() ,
, ![]() �����[�̏W������f�O�͂ƏW���O�̓��[�����g�ł���B
�����[�̏W������f�O�͂ƏW���O�̓��[�����g�ł���B
���U���̈�ʉ��͎O�p���Ƒo�Ȑ����ł��������C
�L���v�f�@�̓����́C�ψʂ��敪�I�������ŋߎ����邱�Ƃɂ���������C
�����ł��ÓI�Ȗ��̎�(5.21)�Ɠ��l�ɁC����݂̕ψʊ���
�ƒ�`�������
�ƒu�����Ƃɂ���B���̎�(10.214)��
��̉��z�d����(10.212)�ɑ�������
�ɂȂ�̂ŁC�C�ӂ̉��z�ψ�
![]() �ɑ��Ă��ꂪ
�������Ȃ���Ȃ�Ȃ����Ƃ���C�^����������
�ɑ��Ă��ꂪ
�������Ȃ���Ȃ�Ȃ����Ƃ���C�^����������
�ƕ\���ł���B�����ɁC�v�f�̕ψʃx�N�g���Ɠ�̊O�̓x�N�g����
�ƒ�`�����B�܂��Ō�̕��z�O�͂̓����ߓ_�O�́i������
���Y����![]() �͗������j�́C��(5.22b)�Ɠ��l��
�͗������j�́C��(5.22b)�Ɠ��l��
�ƒ�`�����B���̒莮���œ��邱�Ƃ��ł��鎿�ʍs��![]() ��
��
�ƒ�`�ł���B�����R�x�n�̏W�����ʍs��i�Ίp�s��j�Ƃ�
�قȂ�C![]() �̂��ׂĂ̐��������̍s��ɂȂ��Ă���B
���̂悤�Ȏ��ʍs����������ʍs��
�ƌĂԂ��Ƃ�����B�܂������s��́C��(5.24)�Ɠ�����
�̂��ׂĂ̐��������̍s��ɂȂ��Ă���B
���̂悤�Ȏ��ʍs����������ʍs��
�ƌĂԂ��Ƃ�����B�܂������s��́C��(5.24)�Ɠ�����
�ƒ�`�����B�v���C����![]() �ɂ�������\���B
�܂��C�S�����ޗ����̂��̂̔S�����f���Œ莮������
�L���v�f�̏ꍇ�ɂ́C���̌����s���Rayleigh�����̎�(10.119)��
�����̍�����ጸ���ɂȂ�
�ɂ�������\���B
�܂��C�S�����ޗ����̂��̂̔S�����f���Œ莮������
�L���v�f�̏ꍇ�ɂ́C���̌����s���Rayleigh�����̎�(10.119)��
�����̍�����ጸ���ɂȂ�
�ƒ�`�ł���B���ׂāC1�v�f�͈�l�f�ʂň�l�ޗ��łł��Ă��邱�Ƃ� ���肵�Ċȗ��������B
��(10.215)�͗v�f�̉^���������Ȃ̂ŁC
���Ƃ͗v�f�Ԃ̘A��������p���āC��-5.3.2
(1)�̒��ڍ����@��p���āC
�S�̍\���̉^����������g�ݗ��Ă�����B
�ŏI�I�ɂ͑����R�x�n�̉^��������(10.95)�ƑS������
�̌`�̉^���������ɂȂ�B�O�̓x�N�g��![]() �ɂ́C
�W���O��
�ɂ́C
�W���O��![]() �ƕ��z�O�͂ɂ�铙���ߓ_�O��
�ƕ��z�O�͂ɂ�铙���ߓ_�O��![]() ��
�������܂Ƃ߂��B
�����R�x�n�ƈقȂ�̂́C���̂悤�ɂ��đS�̍\���̉^����������
�g�ݗ��Ă����ƁC�w�I�ȋ��E�����i���R�x���Œ肳��Ă���
�����j�����̉^���������ɐݒ肵�Ȃ��Ƃ����Ȃ����Ƃł���B
�Ⴆ�C�㎮(10.221)����������
��
�������܂Ƃ߂��B
�����R�x�n�ƈقȂ�̂́C���̂悤�ɂ��đS�̍\���̉^����������
�g�ݗ��Ă����ƁC�w�I�ȋ��E�����i���R�x���Œ肳��Ă���
�����j�����̉^���������ɐݒ肵�Ȃ��Ƃ����Ȃ����Ƃł���B
�Ⴆ�C�㎮(10.221)����������![]() ���R�x��
�^���������ɂȂ��Ă���ƍl���āC���̑�
���R�x��
�^���������ɂȂ��Ă���ƍl���āC���̑�![]() ���R�x���S������Ă���ꍇ�ɂ́C
����ɑΉ�����O�͔͂��͂ɂȂ�̂Ŗ��m���ł���B
�����ŁC���̍s�̕��������C��
���R�x���S������Ă���ꍇ�ɂ́C
����ɑΉ�����O�͔͂��͂ɂȂ�̂Ŗ��m���ł���B
�����ŁC���̍s�̕��������C��![]() ���R�x�̉����x���ɂ��������
���R�x�̉����x���ɂ��������
�ƒu�������邱�Ƃɂ���B�܂�C
�O�̍s��ƊO�̓x�N�g���̐����̂����C
![]() �ɑ���
�ɑ���
�Ƃ��������������C�Ή������![]() ���R�x���S���������ƂɂȂ�B
�����ɁC�Ⴆ��
���R�x���S���������ƂɂȂ�B
�����ɁC�Ⴆ��![]() �͍s��
�͍s��![]() �̑�
�̑�![]() �s��
�s��![]() ����\������B
����\������B
�U����͂ł́C�ŗL�U�����ƐU�����[�h��m�邱�Ƃ��ł��d�v�ł���������C
�܂����R�U����͂�����K�v������B
�O�͂��ɂ��Ă����Ď�������T�����������Ȃ̂�
�ƒu�������B������![]() �͐U����s��ł���B
�������ŊO�̖͂�����(10.221)�ɑ�������
�͐U����s��ł���B
�������ŊO�̖͂�����(10.221)�ɑ�������
�����Ă���������ƂɂȂ�B���������āC
�L�ӂ�![]() �����݂��邽�߂̏�������
�����݂��邽�߂̏�������
�łȂ���Ȃ炸�C���̎����ŗL�U����![]() �����肷��U�����������ɂȂ�B
�܂�C�����R�x�n�̌ŗL�l���ƌ`���I�ɂ͓����`�����Ă���B
�����肷��U�����������ɂȂ�B
�܂�C�����R�x�n�̌ŗL�l���ƌ`���I�ɂ͓����`�����Ă���B
�Ⴆ�Η��[�P���x������1�v�f��p�����ꍇ�ɂ́C�㎮(10.223)�́C
��(10.215)�̑�2, 4�s�����̕�����
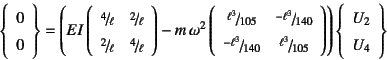
�ƂȂ�̂ŁC�U����������(10.223)��
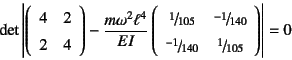
�ƂȂ�B![]() ,
, ![]() �͂��ꂼ��
�͂��ꂼ��![]() ,
, ![]() �̐U���ł���B
�����������
�̐U���ł���B
�����������
�Ƌ��߂邱�Ƃ��ł���B���ꂪ�P���x�����̑�1, 2���̌ŗL�U������
��������̂ŁC��(10.182)�̌������Ɣ�r�����
���x�ɂȂ�B�܂�1���̐U������11%�̌덷�C2���̐U������27%�� �덷�ŋ��߂�ꂽ���Ƃ��Ӗ�����B
�\-10.2�ɂ́C
���[�P���x�����̌ŗL�U�������C�p����v�f���𑝂₵�Ȃ���L���v�f�@��
���߂��̂��̂��������B
�������C�\��![]() �͑�
�͑�![]() ���U�����̌������ƗL���v�f����
��ŁC
���U�����̌������ƗL���v�f����
��ŁC
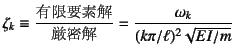 �ƒ�`�����B�v�f����������ɂ��
���̐��x���オ���Ă������Ƃ����炩�ł���B
�H�w�I�ɍł��d�v�ȍŒ�̌ŗL�U�����́C2�v�f�i4���R�x�j��
��1%�����ɂȂ��Ă��邱�Ƃ͋����[���B
�U�����̋ߎ��������������傫���Ȃ�̂́C�ߎ����邱�Ƃɂ����
���f���̕ό`���^�̕ό`���S�����ꂽ���̂ɂȂ��āC
���̌�������̍������傫���Ȃ��Ă��܂�����ł���B
�ƒ�`�����B�v�f����������ɂ��
���̐��x���オ���Ă������Ƃ����炩�ł���B
�H�w�I�ɍł��d�v�ȍŒ�̌ŗL�U�����́C2�v�f�i4���R�x�j��
��1%�����ɂȂ��Ă��邱�Ƃ͋����[���B
�U�����̋ߎ��������������傫���Ȃ�̂́C�ߎ����邱�Ƃɂ����
���f���̕ό`���^�̕ό`���S�����ꂽ���̂ɂȂ��āC
���̌�������̍������傫���Ȃ��Ă��܂�����ł���B
�������C�e�ŗL�U�����ɑΉ�����ŗL�x�N�g���́C�ŗL�U�����[�h�ł���B
�܂�������O�ł��邪�C
�����̒莮���ł�![]() ���邢��
���邢��![]() �ɂ�
����݂Ƃ���݊p�����݂ɕ���ł���̂ŁC
���ۂɕ`�悷��ꍇ�ɂ͒��ӂ��K�v�ł���B
���Ƃ��āC��q�̗��[�P���x�����̗L���v�f��p�������R�U����͂�
����ꂽ�ŗL�x�N�g������C��s�̂���݂������Ō����
�ߎ��̌ŗL�U�����[�h��`���Ă݂悤�B�}-10.52��
����40�v�f�ŕ��������Ƃ��̍ŏ��̎O�̐U�����[�h�ł���B
�ŗL�x�N�g���̂����̂���݂����i�}�ł�
�ɂ�
����݂Ƃ���݊p�����݂ɕ���ł���̂ŁC
���ۂɕ`�悷��ꍇ�ɂ͒��ӂ��K�v�ł���B
���Ƃ��āC��q�̗��[�P���x�����̗L���v�f��p�������R�U����͂�
����ꂽ�ŗL�x�N�g������C��s�̂���݂������Ō����
�ߎ��̌ŗL�U�����[�h��`���Ă݂悤�B�}-10.52��
����40�v�f�ŕ��������Ƃ��̍ŏ��̎O�̐U�����[�h�ł���B
�ŗL�x�N�g���̂����̂���݂����i�}�ł�![]() �ƋL�����j��p����
�ߎ��ł��邪�C�}-10.43������܂ł��Ȃ��C
�������U�����[�h�������Ă���̂����炩�ł���B
�ƋL�����j��p����
�ߎ��ł��邪�C�}-10.43������܂ł��Ȃ��C
�������U�����[�h�������Ă���̂����炩�ł���B
 |
���ɁC�n�k������͂̂悤�Ɏ�����������͂�����ꍇ�ɂ́C
���U�����ꂽ�^��������(10.221)�𑽎��R�x�n�̏ꍇ��
������@�ʼn��������B
�Ⴆ�C��-10.2.3�Ő�����������������
�p����ꍇ�̃t���[�`���[�g��}-10.53�Ɏ������B
��������������Ă������B�܂����̏ꍇ�̗�Ƃ��āC
�P���x������̑��s�d�ɂ��}-10.49�̉����̂����C
�X�p�������̂���݂�2�v�f��4�v�f��
��͂������ʂ�}-10.54�Ɏ������B
���s�d�͂��鎞��![]() ��
��![]() �̈ʒu�ɂ��邪�C
���ꂪ
�̈ʒu�ɂ��邪�C
���ꂪ![]() �Ԗڂ̗v�f��ɂ���Ɣ���ł����ꍇ�C
���̗v�f���[��
�Ԗڂ̗v�f��ɂ���Ɣ���ł����ꍇ�C
���̗v�f���[��![]() ���W��
���W��![]() �ł���Ƃ���ƁC
���̗v�f���̈�֎Ԃ̈ʒu
�ł���Ƃ���ƁC
���̗v�f���̈�֎Ԃ̈ʒu![]() ��
��![]() �ƂȂ�B���������āC
��(10.217)�̓����ߓ_�O�͂̒�`����C
���s�d��Dirac�̃f���^����p����
�ƂȂ�B���������āC
��(10.217)�̓����ߓ_�O�͂̒�`����C
���s�d��Dirac�̃f���^����p����
�ɂ���ĎZ��ł���B�������C����![]() ��1�v�f�̒����ł���B
���[�h��͖@��
��錵�����̈�_������4�v�f�ɂ������̌��ʂ�
�قƂ�Ǐd�Ȃ��Ă��āC2�v�f�ɂ��
�j���̌��ʂ��C�g��}�Ɏ��������x�̍��i�قƂ�Ǐd�Ȃ��Ă����
�v�����j�����Ȃ��B�H�w�I�ɂ�2�v�f��
�\���Ȍ��ʂ����߂��Ă���ƍl������B�}-10.55�ɂ́C
���[�h��͂��ʓ|�ȕs�Ò���̗�Ƃ��āC2�a�ԘA��������֎Ԃ�
���s����ꍇ�́C���̃X�p�������̂���݂��������B
��1�v�f�̒����ł���B
���[�h��͖@��
��錵�����̈�_������4�v�f�ɂ������̌��ʂ�
�قƂ�Ǐd�Ȃ��Ă��āC2�v�f�ɂ��
�j���̌��ʂ��C�g��}�Ɏ��������x�̍��i�قƂ�Ǐd�Ȃ��Ă����
�v�����j�����Ȃ��B�H�w�I�ɂ�2�v�f��
�\���Ȍ��ʂ����߂��Ă���ƍl������B�}-10.55�ɂ́C
���[�h��͂��ʓ|�ȕs�Ò���̗�Ƃ��āC2�a�ԘA��������֎Ԃ�
���s����ꍇ�́C���̃X�p�������̂���݂��������B![]() ��
�E�̃X�p���Ɉړ�����̂ŁC����݂����i������j�Ɉڍs���C
��
�E�̃X�p���Ɉړ�����̂ŁC����݂����i������j�Ɉڍs���C![]() ��
���s�d�͗��̊O�ɏo�āC���̂��Ƃ͎��R�U�������Ă���B
��
���s�d�͗��̊O�ɏo�āC���̂��Ƃ͎��R�U�������Ă���B
�}-10.56(a)�ɂ́C�����Œ�W���O�͂�
���鉞�����������}-10.45�̌��ʂƂ�
��r���C4�v�f�ʼn�͂������ʂ�p���Ď������B
���[�h��͌��ʂ��j���ŕ`���Ă��邪�C�X�p�������̎������������C
��\�I�Ȏ����̂���`����C�قƂ�Ǐd�Ȃ��Ă��āC
�\���Ȑ��x�ŋ��߂��Ă��邱�Ƃ��킩��B
�Ȃ��C����`��́C�ψʊ��̎�(10.214)��
�ߓ_�̂���݂Ƃ���݊p�̗�����p���Ă�萳�m�ɕ`�������̂ł���B
�܂��}-10.56(b)�ɂ́C
�����\���ƊO�͏����ŁC�������܂߂��ꍇ�̉������������B
�����萔��
�ƒ�`���C���̗�ł�
![]() �Ƃ����B
���̒�`�́C��(10.199)��
�Ƃ����B
���̒�`�́C��(10.199)��
![]() ��
��`�Ƃ͎�قȂ�̂Œ��ӂ���B
�j�������[�h��͂ɂ������ł��邪�C�������܂߂����l
���́C�ÓI�Ȃ����
��
��`�Ƃ͎�قȂ�̂Œ��ӂ���B
�j�������[�h��͂ɂ������ł��邪�C�������܂߂����l
���́C�ÓI�Ȃ����![]() �i�c����1�j�ɏ��X�ɋ߂Â��Ă������Ƃ������Ă���B
����
�i�c����1�j�ɏ��X�ɋ߂Â��Ă������Ƃ������Ă���B
����![]() ��
��![]() �̉ו���
�̉ו���
![]() �ɒu���܂܂ɂ���������
���Ȃ̂ŁC�ŏI�I�ɂ͂��̐ÓI����݂Ɏ������Ă����B
�ɒu���܂܂ɂ���������
���Ȃ̂ŁC�ŏI�I�ɂ͂��̐ÓI����݂Ɏ������Ă����B
���̂悤�ɁC���l��͂ɂ���āC�ǂ�ȊO�͂ɑ��鉞�����v�Z�ł��� �킯�����C�������ӂ��ė~�����̂́C���ꂪ�K���������ڐv�ɗL�p�� ����^���Ă����Ƃ͌���Ȃ����Ƃł���B �ނ���C�K�v�ɉ����đ�z���郂�[�h��T���C ���̐����̉������X�ɔ�r��������C�v�ɂ͖𗧂̂ł���B ���������āC�O�߂܂ł̃��[�h��͂ɂ��Ă̗������d�v�ƂȂ�B ����3�����̎��\�����̂悤�ɁC�Ȃ������ł͂Ȃ��˂��ꓙ���܂� ���G�ȐU��������ꍇ�ɂ́C���ڂ��Ă���v�f�ʂ̉��͂� ���傳����U�����[�h��T���o���C���̃��[�h�𐧌䂷��悤�� �v�ύX������K�v�����邾�낤�B ���̂悤�ȏꍇ�C���R�Ƃ��̒f�ʂ̐��l�I�ȉ����߂Ă�����C ���[�h��͖@�̂悤�ȍl�@�����݂邱�Ƃ̕����L�p�ł��낤�B �����Ă��̏ꍇ�C���l��͂Ƃ����̂́C����P�[�X�X�^�f�B�� �Ȃ��Ă��܂��Ă���\��������̂Œ��ӂ��ė~�����B
�O�߂܂łɎ��������Ɠ��l�C
�g���X���ނ̂悤�Ȏ��͂Œ�R����_���ނ������R�x�U���n�Ƀ��f�����ł���B
�������ƈꏏ�ɗp���邱�Ƃɂ���ĔC�ӂ̕��ʍ��g�̐U����͂��\��
�Ȃ邾�낤�B
�����ł܂��C�_���ނ̗L���v�f�^�������������߂Ă������B
��(5.13)�̉��z�d�����Ɋ������������邱�Ƃɂ���āC
����![]() ��1�v�f�̉��z�d������
��1�v�f�̉��z�d������
�ƂȂ�B������![]() �͒f�ʐςł���C
�͒f�ʐςł���C![]() �͎������̒P�ʒ����������
���z�O�́C
�͎������̒P�ʒ����������
���z�O�́C![]() , (
, (![]() )�͒[���̎��O�͂ł���B
�p����ψʊ��͐ÓI�Ȗ��̎�(5.15)�Ɠ����������ł�������
)�͒[���̎��O�͂ł���B
�p����ψʊ��͐ÓI�Ȗ��̎�(5.15)�Ɠ����������ł�������
�Ƃ��悤�B�������̉��z�d����(10.225)�ɑ�����Đ�������ƁC
���U�����ꂽ�^����������
�ƕ\�����Ƃ��ł���B�����ɁC�v�f�̕ψʃx�N�g���Ɠ�̊O�̓x�N�g����
�ƒ�`�����B�܂��Ō�̕��z�O�͂̓����ߓ_�O�͂́C��(5.16)�Ɠ��l��
�ƒ�`�����B���̒莮���œ��邱�Ƃ��ł��鎿�ʍs��![]() ��
��
�ƒ�`�ł��C���̏ꍇ�Ɠ��l�������ʍs��ɂȂ��Ă���B
�܂������s��́C��(5.17)�Ɠ�����
�ƒ�`�����B�v���C����![]() �ɂ�������\���B
���ׂāC1�v�f�͈�l�f�ʂň�l�ޗ��łł��Ă��邱�Ƃ����肵�Ċȗ��������B
�㎮(10.227)�́C��-11.1��1������
�g���C�܂�_�ⓛ�̒��̑a���g���̗L���v�f��͂Ɏg����B
�܂��C
�ɂ�������\���B
���ׂāC1�v�f�͈�l�f�ʂň�l�ޗ��łł��Ă��邱�Ƃ����肵�Ċȗ��������B
�㎮(10.227)�́C��-11.1��1������
�g���C�܂�_�ⓛ�̒��̑a���g���̗L���v�f��͂Ɏg����B
�܂��C![]() ��
��![]() �Œu��������ΐ�-10.3.1��
���̐U���̗L���v�f�^���������ł�����B
�Œu��������ΐ�-10.3.1��
���̐U���̗L���v�f�^���������ł�����B
�S�������ɂ��ẮC�Ⴆ���̍ޗ����f����
��(10.194)�Ɠ����悤�ɍl���Ă������̂�
�Ƃ�������B������![]() �͍ޗ��̔S���W���ł���B
���̃��f���̏ꍇ�ɂ́C���̌����s���
�͍ޗ��̔S���W���ł���B
���̃��f���̏ꍇ�ɂ́C���̌����s���
�ƒ�`�ł���B
���ʍ��g�́C���k�͂���Ȃ����ނ��C�ӂ̕����ɔz�u���ꂽ���̂�
���邪�C��-5.3.4�ɂ���悤�ɍl����C
���̗L���v�f�^�����������莮���ł���B
�����ŁC��̎�(10.227)��
�Ȃ��̎�(10.215)�����̂����Ă݂悤�B
�������ȒP�̂��߂Ɍ����ƕ��z�O�͖͂�������B
���g�̊e���ނ͂��ꂼ��ʁX�̕�����������
�z�u����Ă���̂ŁC�}-10.57�̂悤��
�v�f��![]() -
-![]() ���W�n�ƑS�̍��W�n�Ƃ̌�����
�Ⴂ���p�x
���W�n�ƑS�̍��W�n�Ƃ̌�����
�Ⴂ���p�x![]() �Œ�`���Ă����B
���̗v�f���W�n�ł̎��ʍs��ƍ����s��͂��ꂼ��C
��(10.218)�Ǝ�(10.230)���C������
��(10.219)�Ǝ�(10.231)�����̂�����
�Œ�`���Ă����B
���̗v�f���W�n�ł̎��ʍs��ƍ����s��͂��ꂼ��C
��(10.218)�Ǝ�(10.230)���C������
��(10.219)�Ǝ�(10.231)�����̂�����
�ƒ�`�ł���B
����ɑ��đS��![]() -
-![]() ���W�n�ɂ��������g�L���v�f�̉^��������
��
���W�n�ɂ��������g�L���v�f�̉^��������
��
�ƕ\�����Ƃ��ł���B������
�ƒ�`�����B�����đS�̍��W�n�̎��ʍs��ƍ����s��́C
��(10.234)�̏��s���p����
�ƒ�`�ł���B�����ɁC���W�ϊ��s���
�ƒ�`�����B
�ŏI�I�ȉ^���������͑����R�x�n�̂���Ɠ����Ȃ̂ŁC
�O�߂ł��������悤�Ȏ��R�U����͂�������������͂����l�ɉ\�ł���B
�����ł͎��R�U�������Ɍ��肵�āC��{�I�ȍ\���n�̌ŗL�U������
�U�����[�h���������Ƃɂ���āC���̓�����������Ă������B
�ŏ��ɁC��^���g����͂����̂��}-10.58�ł���B
�����ł��ŗL�x�N�g���̂����̂���݊p
![]() ��
�������C�ψʐ���������p���Ē����Ō���ŕ`�����ߎ��I�ȐU�����[�h�ł���B
�܂��ŗL�x�N�g���̕ψʂ̒l�����������Č֒������}�ɂȂ��Ă���B
�܂��������������̍��E�Ώ̂Ȗ�^���g��
��͂����̂��}-10.58(a)�ł���B
�Ή�����ŗL�U������\-10.3�̑�2�J�����Ɏ����Ă������B
���Ɨ������ꂼ��40�v�f�ŋߎ����Ă���̂ŁC
�Z�̋��E�����̂��Ƃ��l������C117���R�x�̑����R�x�n�ŋߎ��������ƂɂȂ�B
���Ɨ��͓�������
��
�������C�ψʐ���������p���Ē����Ō���ŕ`�����ߎ��I�ȐU�����[�h�ł���B
�܂��ŗL�x�N�g���̕ψʂ̒l�����������Č֒������}�ɂȂ��Ă���B
�܂��������������̍��E�Ώ̂Ȗ�^���g��
��͂����̂��}-10.58(a)�ł���B
�Ή�����ŗL�U������\-10.3�̑�2�J�����Ɏ����Ă������B
���Ɨ������ꂼ��40�v�f�ŋߎ����Ă���̂ŁC
�Z�̋��E�����̂��Ƃ��l������C117���R�x�̑����R�x�n�ŋߎ��������ƂɂȂ�B
���Ɨ��͓�������![]() �ł���Ƃ��C
���̒����Œ�`�����ג���
�ł���Ƃ��C
���̒����Œ�`�����ג���![]() ��100�Ƃ����B
������
��100�Ƃ����B
������![]() �͒f�ʂ̉�]���a
�͒f�ʂ̉�]���a
![]() �ł���B
�ł���B
���[�P���x�����̏ꍇ�ƈقȂ�C��3���ŗL�U�����͂���قǑ傫���Ȃ��Ă��Ȃ��B ����́C3���̐U�����[�h��2���̐U�����[�h�̈ꕔ���t�����ɂȂ������炢�� �������������߂ł���B�܂���4���ŗL�U������3���̂�����߂��B �����3����4���̐U�����[�h���ގ����Ă��邩��ł���B ���̂悤�ɁC�U�����[�h�����E����������\�����āC�ǂ̂悤�Ȏ����� �ŗL�U�������ߕt���̂��𐄑��ł���悤�ɂȂ�ƁC ���U����\���n��v���邱�Ƃ��ł���悤�ɂȂ邩������Ȃ���B
���ɁC�E�̒������̔����̍��������Ȃ���Ώ̂Ȗ�^���g�� ��͂������ʂ��}-10.58(b)�ł���B �ŗL�U�����͕\-10.3�̑�3�J�����Ɏ������B ���x�͑�3����4���̐U����������Ă���B�����4���̐U�����[�h�� ���Ȃ蕡�G�Ȃ��̂ɂȂ������Ƃ������ł���B ����ɂ���āC��5���̐U�������傫���Ȃ����ƍl������B
���ɁC���ɐ�2�q���W�A�[�`��̍\����
�ΏۂƂ��Ă݂��B�}-10.59�̍���ɂ���̂��C
���p![]() ��30�x�̐A�[�`�������Ă���B
���̉~�ʂ̒�����
��30�x�̐A�[�`�������Ă���B
���̉~�ʂ̒�����![]() �Ƃ��āC�����p�����ג����
�Ƃ��āC�����p�����ג����
![]() �Ɛݒ肵�C
���̉~�ʂ�40�̌��Ō���ŋߎ����Ă���B�}-10.59(a)�ɂ�
���̓��p��30�x�̏ꍇ�̐U�����[�h���������B�����[�����ƂɁC�\���n���Ώ̂ł���ɂ�������炸�C�Œ�̑�1����
�U�����[�h�͔��Ώ̂ł���B����́C�\���n���̂��̂̌`��������
��1���Ώ̐U�����[�h�Ɠ����ł��邱�Ƃ������ł���B�\-10.3��
��4�J�����ɂ���ŗL�U����������ƁC
���[�P���x�����ɔ�ׂāC���ꂼ�ꂪ���܂藣��Ă��Ȃ��B
�܂�C���U�U�������ߕt���Ă��邱�ƂɂȂ�C�ΐU����
�v����������Ȃ邱�Ƃ������Ă���B
�Ɛݒ肵�C
���̉~�ʂ�40�̌��Ō���ŋߎ����Ă���B�}-10.59(a)�ɂ�
���̓��p��30�x�̏ꍇ�̐U�����[�h���������B�����[�����ƂɁC�\���n���Ώ̂ł���ɂ�������炸�C�Œ�̑�1����
�U�����[�h�͔��Ώ̂ł���B����́C�\���n���̂��̂̌`��������
��1���Ώ̐U�����[�h�Ɠ����ł��邱�Ƃ������ł���B�\-10.3��
��4�J�����ɂ���ŗL�U����������ƁC
���[�P���x�����ɔ�ׂāC���ꂼ�ꂪ���܂藣��Ă��Ȃ��B
�܂�C���U�U�������ߕt���Ă��邱�ƂɂȂ�C�ΐU����
�v����������Ȃ邱�Ƃ������Ă���B
����ɑ��C���p��22.5�x�ɂȂ�悤�ȁC�����ƐA�[�`��̍\����
�ꍇ�ɂ́C�}-10.59(b)�ɂ���悤�ɁC
�Œ�̑�1���U�����[�h���Ώ̂ɂȂ�B���̓�̐}�����Ă����ɂ킩��悤�ɁC
���̓��p�̈Ⴂ�ɂ���āC
��1����2���̃��[�h�������t�]���Ă��邱�Ƃ����炩�ł���B
���́C
![]() �x�ŏ��������̓�̌ŗL�U������
��v�i
�x�ŏ��������̓�̌ŗL�U������
��v�i
![]() �j����B
���̂��߁C���̊p�x�ɋ߂�22.5�x�̏ꍇ�̌ŗL�U������
���z��\-10.3�̑�5�J�����Ō���ƁC
���������̓�̐U�������ߕt���Ă���̂��[���������B
�j����B
���̂��߁C���̊p�x�ɋ߂�22.5�x�̏ꍇ�̌ŗL�U������
���z��\-10.3�̑�5�J�����Ō���ƁC
���������̓�̐U�������ߕt���Ă���̂��[���������B
�����Ŏ��ɁC�Œ�A�[�`�̏ꍇ�̓��p�Ə��������̓�̌ŗL�U������
�W�����߂Ă݂��̂��}-10.60�ł���B
�������A�[�`�̓��p�ł���C��40.092�x�����ɁC
�Œ�̐U�����[�h�̑Ώ̂Ɣ��Ώ̂�����ւ���Ă���B
������![]() ��45�x�̏ꍇ��36�x�̏ꍇ�ɂ��āC
�ŗL�U�����[�h��}-10.61�ɁC
�ŗL�U������\-10.3�̑�6, 7�J�����Ɏ������B
���炩�ɁC��1����2���̐U�����[�h������ւ���Ă���B
���p��45�x�̏ꍇ�ɂ́C��2, 3, 5�����قڑΏ̂ő�1, 4�������Ώ̂ɂȂ�B
����ɑ�36�x�̏ꍇ�ɂ́C��2, 4�������Ώ̂ł���B
������ɂ��Ă��C�\-10.3���������ɔ�ׂ��
���炩�Ȃ悤�ɁC�A�[�`��̍\���̏��������̐U�����́C
��^���g�◼�[�P���x�����ɔ�ׂĂ��݂��ɋߕt���Ă��邱�Ƃ�
���ӂ���K�v�����邾�낤�B
����Ɏ��ۂ̎Љ��Ս\���͂��ׂė��̓I�Ȃ��̂ł���C
�����ƕ��G�ȕό`�̎��R�x��L���Ă��邱�Ƃ���C
�ŗL�U�������m���ߕt�����Ƃ͕��ʂɊώ@�����ł���B
���[�P���x�����̂悤�Ȃ������ꂽ�ŗL�U�����̕��z�����邱�Ƃ�
�����H�ł��邱�Ƃɂ͏\�����ӂ���K�v������B
��45�x�̏ꍇ��36�x�̏ꍇ�ɂ��āC
�ŗL�U�����[�h��}-10.61�ɁC
�ŗL�U������\-10.3�̑�6, 7�J�����Ɏ������B
���炩�ɁC��1����2���̐U�����[�h������ւ���Ă���B
���p��45�x�̏ꍇ�ɂ́C��2, 3, 5�����قڑΏ̂ő�1, 4�������Ώ̂ɂȂ�B
����ɑ�36�x�̏ꍇ�ɂ́C��2, 4�������Ώ̂ł���B
������ɂ��Ă��C�\-10.3���������ɔ�ׂ��
���炩�Ȃ悤�ɁC�A�[�`��̍\���̏��������̐U�����́C
��^���g�◼�[�P���x�����ɔ�ׂĂ��݂��ɋߕt���Ă��邱�Ƃ�
���ӂ���K�v�����邾�낤�B
����Ɏ��ۂ̎Љ��Ս\���͂��ׂė��̓I�Ȃ��̂ł���C
�����ƕ��G�ȕό`�̎��R�x��L���Ă��邱�Ƃ���C
�ŗL�U�������m���ߕt�����Ƃ͕��ʂɊώ@�����ł���B
���[�P���x�����̂悤�Ȃ������ꂽ�ŗL�U�����̕��z�����邱�Ƃ�
�����H�ł��邱�Ƃɂ͏\�����ӂ���K�v������B
���́C��(10.169)�̃��[�����g�̂荇�����l�����Ƃ��ɂ́C
���I�Ȍ��ʂ����Ă����B
�܂�C��]�^���̉^����������
��(10.4)�̂悤��Newton�̖@������������͂��Ȃ̂ɁC
��]���������Ă����B��]����������ƁC
�f�ʂ̉�]�p������݊p�Ɠ����Ȃ̂ŁC��(10.169)�̑����
���������^���������ɂȂ�B�����̊������[�����g![]() ��
��(10.5)�̒�`����̒f�ʂɓK�p����C����
��
��(10.5)�̒�`����̒f�ʂɓK�p����C����![]() �������
�������
�ƂȂ�B������![]() �͖��x�ŁC
�͖��x�ŁC![]() �͒f��2�����[�����g�ł���B
���������āC���[�����g�̉^���������͖{����
�͒f��2�����[�����g�ł���B
���������āC���[�����g�̉^���������͖{����
�Ƃ��Ȃ���Ȃ�Ȃ��B���̉E�ӂ������]����
�ƌĂ�ł���B�������(10.168)�̂���f�͂�
���Ẳ^���������ɑ������C��]�������l������
���̉^���������́C��l�f�ʁE��l�ޗ��̏ꍇ�ɂ�
�ƂȂ�B�܂����E������(10.197)���C����f�͂̎���
�Œu�������Ȃ���Ȃ�Ȃ��B
���̉�]�����̒�ʓI�ȉe���͎��̐߂Ŏ����B
�����ł͂��̓����𖾂炩�ɂ��邽�߂ɁC����݂Əꏊ�̓Ɨ��ϐ���
���̒���![]() �Ŗ����������Ă����B�܂�
�Ŗ����������Ă����B�܂�
�ƒ�`���āC��̉^��������(10.240)������������
�ƂȂ�B������![]() �͎�(6.37a)�Œ�`�����ג���
�͎�(6.37a)�Œ�`�����ג���
(10.243)
�ł���B![]() �͒f�ʂ���]���a
�ƌĂ�C�f�ʐ��@���\���钷���ł���B
�^���������̍��ӂ̑劇�ʓ��ɂ���ŏ���3����
���ʂ̗����_�̉^���������̍��ł��邱�Ƃ�O���ɒu���ƁC
��4���̉�]�������͍ג���
�͒f�ʂ���]���a
�ƌĂ�C�f�ʐ��@���\���钷���ł���B
�^���������̍��ӂ̑劇�ʓ��ɂ���ŏ���3����
���ʂ̗����_�̉^���������̍��ł��邱�Ƃ�O���ɒu���ƁC
��4���̉�]�������͍ג���![]() ���傫���Ȃ��
��r�I�������Ȃ��Ė����ł��邱�Ƃ��킩��B
�܂�C��]�����̉e���́C�ג������ł͖������Ă��������ƂɂȂ�B
���邢�́C�����I�ɒZ�����̐U�����ۂɑ������鍂���g�U����
�ΏۂƂ���ꍇ�ɂ́C��]�����̉e�����ł��Ȃ��Ȃ�\����
���邱�Ƃ��������Ă���B
���傫���Ȃ��
��r�I�������Ȃ��Ė����ł��邱�Ƃ��킩��B
�܂�C��]�����̉e���́C�ג������ł͖������Ă��������ƂɂȂ�B
���邢�́C�����I�ɒZ�����̐U�����ۂɑ������鍂���g�U����
�ΏۂƂ���ꍇ�ɂ́C��]�����̉e�����ł��Ȃ��Ȃ�\����
���邱�Ƃ��������Ă���B
�����ג��䂪���������ʼn�]�����̉e�����傫���Ȃ�̂ł���C
������C�����Z���ꍇ�ɍl�����Ȃ���Ȃ�Ȃ��Ȃ邹��f�ό`��
�e���������ł��Ȃ��Ȃ邱�Ƃ��\�z�����B
����f�ό`���l�����������_�̑�\��Timoshenko�����_�ł��낤�B
�����ł́C����f�ό`�̉e����Timoshenko���̃��f���ōl�����C
��]�������l�������ꍇ�̉^�����������C
���̉e�����ʓI�Ɏ����Ă����BTimoshenko���̉^�����
�L�q�����̂��}-10.62�ł���B
�}���疾�炩�Ȃ悤�ɁC�f�ʓ��C�ӓ_��![]() ,
, ![]() �����ψʐ�����
�����ψʂ͈͓̔��ŁCBernoulli-Euler���̎�(4.3)�̑����
�����ψʐ�����
�����ψʂ͈͓̔��ŁCBernoulli-Euler���̎�(4.3)�̑����
�ƂȂ�B������![]() �́C���̂���݊p�ł͂Ȃ��f�ʂ�
��]�p��\���Ă��āC���̂���݊p�ƒf�ʂ̉�]�p�̍�
�́C���̂���݊p�ł͂Ȃ��f�ʂ�
��]�p��\���Ă��āC���̂���݊p�ƒf�ʂ̉�]�p�̍�
��Bernoulli-Euler���ł͖������Ă�������f�ό`�ł���B
�莮���̏ڍׂ͕t�^-D�Ɏ������B�}-10.62��
�����C�Ȃ��ɂ��Ă̐����݂̂������ł͍l���邱�Ƃɂ���ƁC
��]�������܂߂��^����������
�ƂȂ�B�܂�����f�͂ƋȂ����[�����g��
�Ƃ����W�ɂȂ��Ă���B![]() �͂���f�e���W���ł���B
�͂���f�e���W���ł���B![]() �́C
���ۂɂ͐}-4.68�̂悤�ɒf�ʓ���
���l�ɕ��z����͂��̂���f�ό`���C�f�ʓ�����
����f�ό`
�́C
���ۂɂ͐}-4.68�̂悤�ɒf�ʓ���
���l�ɕ��z����͂��̂���f�ό`���C�f�ʓ�����
����f�ό`![]() �ŋߎ��������Ƃ�₤���߂̌W���ł���B�l���̂��̂�
�f�ʌ`���Poisson��
�ŋߎ��������Ƃ�₤���߂̌W���ł���B�l���̂��̂�
�f�ʌ`���Poisson��![]() �Ɉˑ�����萔[16]�ł���B�Ⴆ��
�Ɉˑ�����萔[16]�ł���B�Ⴆ��
�Ƃ������l�����B���E������
�ƂȂ�B������![]() ��p.
��p.![]() �ɍČf����
��(4.24)��
��`�����L���ł���C
�ɍČf����
��(4.24)��
��`�����L���ł���C![]() ���͒[���ŗ^����ψʗʂł���B
��]�p�ɂ��Ă̋��E�����ɂ��ẮC
���͒[���ŗ^����ψʗʂł���B
��]�p�ɂ��Ă̋��E�����ɂ��ẮC![]() ���̂��̂�
���̂��̂�![]() ��
�^����悤�Ȃ��Ƃ͂ł��Ȃ����C
����2�҂����ԍډד_�⒆�Ԏx�_�ŘA���ɂȂ�K�v���������Ƃ�
���ӂ���B
��
�^����悤�Ȃ��Ƃ͂ł��Ȃ����C
����2�҂����ԍډד_�⒆�Ԏx�_�ŘA���ɂȂ�K�v���������Ƃ�
���ӂ���B
��(10.247) (10.248)����![]() ,
, ![]() ��
��������ƁC
��
��������ƁC![]() ������������(10.242)��
������������(10.242)��![]() �ŕ\����
�^����������
�ŕ\����
�^����������
�ƂȂ�B�����ł́C![]() �ƁC
��(10.242)�̖����������ꂽ�Ɨ��ϐ�
�ƁC
��(10.242)�̖����������ꂽ�Ɨ��ϐ�![]() ��p���Ă���B
�܂�
��p������B
�܂�![]() �͎�(10.244a)�Œ�`�����ג���ł���B
�ŏ��̑劇�ʂ�Bernoulli-Euler���̕����C�Ō�̑劇�ʂ�Timoshenko����
�����ł���B�܂���̑劇�ʂ̊Ԃ̍��́C�O�߂�Bernoulli-Euler����
�����]�����̍��ł���B�܂�
�͎�(10.244a)�Œ�`�����ג���ł���B
�ŏ��̑劇�ʂ�Bernoulli-Euler���̕����C�Ō�̑劇�ʂ�Timoshenko����
�����ł���B�܂���̑劇�ʂ̊Ԃ̍��́C�O�߂�Bernoulli-Euler����
�����]�����̍��ł���B�܂�
![]() �́C
��(4.85a)�Œ�`���ꂽ�W����
�́C
��(4.85a)�Œ�`���ꂽ�W����
�ƒ�`����Ă���B
![]() ���ג���
�ɑ������邩��C
�ג������ł�
���ג���
�ɑ������邩��C
�ג������ł�
![]() ����r�I�������Ȃ�̂ŁC
����f�ό`�̉e������]�����Ɠ��l�ɖ����ł��邱�Ƃ��킩��B
����r�I�������Ȃ�̂ŁC
����f�ό`�̉e������]�����Ɠ��l�ɖ����ł��邱�Ƃ��킩��B
�ŗL�U���������߂邽�߂ɁC���z�O�͂��������̂Ƃ��āC����݂�
�ƒu���āC��̉^��������(10.251)�ɑ�����Đ��������
�ƂȂ�B�����ɁC�v���C����![]() �Ɋւ��������\��
�Ɋւ��������\��
�ƒ�`�����B�����![]() �ƒu�����Ƃɂ���āC������������
�ƒu�����Ƃɂ���āC������������
�ƂȂ�̂ŁC��������
�Ƌ��߂���B���̍���
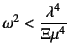 �̂Ƃ��C
��͎���
�̂Ƃ��C
��͎���![]() �ł����������
�ł����������
![]() �ɂȂ�B
�����͏㎮�̕������̑O�̕��������̕�
�ɂȂ�B
�����͏㎮�̕������̑O�̕��������̕�
�ł���B���������āC��ʉ���
�Ƌ��߂���B
��̓I�ȐU���������߂邽�߂ɁC�ȒP�ȒP���x������ΏۂƂ���B
���E�����͎�(10.250)����C���[��
�ƂȂ�̂ŁC��(![]() )�̈�ʉ��������Đ��������
)�̈�ʉ��������Đ��������
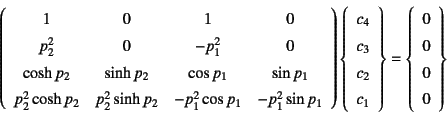
�ƂȂ�B�Ӗ��̂�����ɂȂ邽�߂ɁC�W���s��̍s����ɂȂ������
�ƂȂ�B���������āC�ŗL�U������
��������ł���C![]() �������s��ɂȂ�̂ŁC
�ŗL�U�����[�h��
�������s��ɂȂ�̂ŁC
�ŗL�U�����[�h��![]() �ɂȂ�B
���̎�����(
�ɂȂ�B
���̎�����(![]() )�ɑ�����Đ��������
)�ɑ�����Đ��������
�ƂȂ�B������
�ƒ�`�����B�����̂��鍀����]�����̉e���̍��ł���C![]() �̕t��������
����f�ό`�̉e���̍��ł���B�܂�C
�̕t��������
����f�ό`�̉e���̍��ł���B�܂�C![]() �Ƃ��āC
�����̍������邱�Ƃɂ���āC��]����������Bernoulli-Euler����
�ŗL�U������
�Ƃ��āC
�����̍������邱�Ƃɂ���āC��]����������Bernoulli-Euler����
�ŗL�U������![]() �ɂȂ�B
��̗�Ƃ��ċ�`�f�ʂ̗���ΏۂƂ��C
��(3.44)�Ǝ�(10.249)����
�ɂȂ�B
��̗�Ƃ��ċ�`�f�ʂ̗���ΏۂƂ��C
��(3.44)�Ǝ�(10.249)����
�ƒu���āC�|�A�\�����![]() �Ƃ����Ƃ��́C1������4����
�ŗL�U������}-10.63�Ɏ������B
�ג��䂪�������Ȃ��ĒZ�����ɂȂ�Ȃ�قǁCBernoulli-Euler����
�ŗL�U������菬�����Ȃ�B�܂������̐U�����قǁC�������Ȃ�
�e���͑傫���Ȃ��Ă���B
�����̏ꍇ�́C�ג���͏������Ă�30���炢�ł͂Ȃ����Ǝv����̂ŁC2����
�ŗL�U�����܂łȂ�10%���炢�̍������������C�����R���N���[�g���̂悤��
�ꍇ�ɂ́C�����������e�����l���Ȃ��Ƃ܂����̂ł͂Ȃ����Ǝv�����C
�ǂ����낤�B
�Ƃ����Ƃ��́C1������4����
�ŗL�U������}-10.63�Ɏ������B
�ג��䂪�������Ȃ��ĒZ�����ɂȂ�Ȃ�قǁCBernoulli-Euler����
�ŗL�U������菬�����Ȃ�B�܂������̐U�����قǁC�������Ȃ�
�e���͑傫���Ȃ��Ă���B
�����̏ꍇ�́C�ג���͏������Ă�30���炢�ł͂Ȃ����Ǝv����̂ŁC2����
�ŗL�U�����܂łȂ�10%���炢�̍������������C�����R���N���[�g���̂悤��
�ꍇ�ɂ́C�����������e�����l���Ȃ��Ƃ܂����̂ł͂Ȃ����Ǝv�����C
�ǂ����낤�B