最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
振り子の運動方程式(10.6)を見れば明らかなように,
回転角![]() が小さいものとしてsine関数を近似していた。
このように,現実問題は非線形であるにもかかわらず,それが線形近似の範囲で
取り扱うことができるものとして線形理論の範囲で構造力学や材料力学を
使うことの方が多い。非線形の理屈が重要になるものの代表は,
例えば章-6の座屈理論で考慮する必要がある
幾何学的非線形性と,章-9の塑性論で考慮すべき
材料学的非線形性であろう。
しかしながら,この二つの非線形性をそのまま振動問題に
組み込むことは非常に難しい。
ここでは,そういった非線形性が示すであろう振動特性について,
電気回路等で知られているような問題も含めて考察するために,
主に古典的な振動問題の代表的な非線形問題を取り上げ,
その解析法としての
摂動法を紹介したい。なおこの節は,Northwestern大学Davis教授(1980年頃当時)
の `Asymptotic and Perturbation Methods in Applied Mathematics' の
講義ノート10.12を参考にした。
が小さいものとしてsine関数を近似していた。
このように,現実問題は非線形であるにもかかわらず,それが線形近似の範囲で
取り扱うことができるものとして線形理論の範囲で構造力学や材料力学を
使うことの方が多い。非線形の理屈が重要になるものの代表は,
例えば章-6の座屈理論で考慮する必要がある
幾何学的非線形性と,章-9の塑性論で考慮すべき
材料学的非線形性であろう。
しかしながら,この二つの非線形性をそのまま振動問題に
組み込むことは非常に難しい。
ここでは,そういった非線形性が示すであろう振動特性について,
電気回路等で知られているような問題も含めて考察するために,
主に古典的な振動問題の代表的な非線形問題を取り上げ,
その解析法としての
摂動法を紹介したい。なおこの節は,Northwestern大学Davis教授(1980年頃当時)
の `Asymptotic and Perturbation Methods in Applied Mathematics' の
講義ノート10.12を参考にした。
振り子の運動方程式を式(10.6)のようには近似しない場合には,
その正しい運動方程式は
となる。初期条件は例えば
となる。この初期位置![]() や初速
や初速![]() が大きいと,運動方程式のsine関数は
近似できなくなる。
が大きいと,運動方程式のsine関数は
近似できなくなる。
最初は,固体摩擦振動を
検討した節-10.1.2 (3)で
用いた位相平面
上で,定性的な特性を考えてみよう。まず式(10.13)で
定義された![]() を用いて,
運動方程式(10.255)に
を用いて,
運動方程式(10.255)に![]() を乗じると
を乗じると
となるので,積分すれば位相平面上の運動が
と表されることになる。
初期条件を代入して
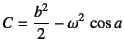 である。
この式(10.257)を
である。
この式(10.257)を![]() 倍すれば,それは高校の物理で
使ったことのある式になる。つまり,第1項は
倍すれば,それは高校の物理で
使ったことのある式になる。つまり,第1項は
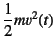 ,
(
,
(
![]() )の運動エネルギであり,
第2項は
)の運動エネルギであり,
第2項は
![]() という
回転中心レベルを基準にした位置エネルギであるから,エネルギ保存則である。
種々の初期条件で描いたのが図-10.64である。
例えば初速が零で初期位置が
という
回転中心レベルを基準にした位置エネルギであるから,エネルギ保存則である。
種々の初期条件で描いたのが図-10.64である。
例えば初速が零で初期位置が![]() より小さい場合には,原点を中心とした
時計回りの軌跡
を描く。
初期位置が十分小さい場合には,線形理論の軌跡の式(10.28)で
示したように,ほぼ楕円状の軌跡を描く。
もちろん
より小さい場合には,原点を中心とした
時計回りの軌跡
を描く。
初期位置が十分小さい場合には,線形理論の軌跡の式(10.28)で
示したように,ほぼ楕円状の軌跡を描く。
もちろん![]() が
が![]() の偶数倍の位置を
中心とする楕円軌跡も存在する。いずれも左右に振れる振り子運動である。
また後述の図-10.65にあるように,
初期位置
の偶数倍の位置を
中心とする楕円軌跡も存在する。いずれも左右に振れる振り子運動である。
また後述の図-10.65にあるように,
初期位置![]() から始まる振動の軌跡は,
横軸上で滑らかな軌跡にならないのは興味深い。
さらに初速を大きくした場合には,
楕円のような軌跡の上下に描いたように,一方向に回転し続けて
振り子運動にはならないことを示している。
から始まる振動の軌跡は,
横軸上で滑らかな軌跡にならないのは興味深い。
さらに初速を大きくした場合には,
楕円のような軌跡の上下に描いたように,一方向に回転し続けて
振り子運動にはならないことを示している。
次の節では,振り子運動の定量的な把握のために摂動法
というものを用いるのであるが,まず,摂動法そのものの
基本的なところを説明しよう。
そのために,摂動法を代数方程式に用いた例を示す。
以下,
![]() とする。最初の例では
とする。最初の例では
を解く。正解はもちろん
![]() である。
ここでは,解を
である。
ここでは,解を![]() で漸近展開で近似し
で漸近展開で近似し
と置くことにする。
記号![]() は,p.
は,p.![]() の脚注で定義したLandauの記号である。
これを上の代数方程式に代入して
の脚注で定義したLandauの記号である。
これを上の代数方程式に代入して![]() のべき順に整理すると
のべき順に整理すると
となる。したがって,各![]() の係数を零とすることによって
の係数を零とすることによって
と求められることから,解は
である。上の正解の平方根をTaylor展開すれば明らかなように,ここまでは 正解と一致している。このように,ある鍵となるパラメータで 漸近展開して解を求める方法が摂動法である。
次の例として,同じような代数方程式
を対象としてみよう。上の例と同様の漸近展開すると
となるが,次のべき乗は
となり失敗する。しかし,これは当然だろう。というのも,
正解は
![]() だからである。
正解を知っているなら,漸近展開は
だからである。
正解を知っているなら,漸近展開は
![]() のべき乗で
与えなければならないことは明らかである。つまり
のべき乗で
与えなければならないことは明らかである。つまり
と置いて,上の方程式に代入すると,![]() は上と同じなので
は上と同じなので![]() であり,
それ以外が
であり,
それ以外が
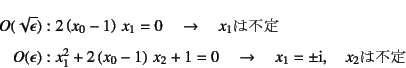
となった上で,高次の項をさらに演算すると,![]() , (
, (![]() )を得る。
これは正解である。
このように,どのような漸近展開をするか等の工夫が必要ではあるものの,
べき乗の係数を求めることによって正解を得る可能性があることがわかる。
)を得る。
これは正解である。
このように,どのような漸近展開をするか等の工夫が必要ではあるものの,
べき乗の係数を求めることによって正解を得る可能性があることがわかる。
最後に,最も高次な項に微小パラメータ![]() がある場合
がある場合
を解いておこう。この問題では,![]() を無視することによって,
この問題の特性を支配している最も重要な項が消えてしまうことが問題になる。
正解は
を無視することによって,
この問題の特性を支配している最も重要な項が消えてしまうことが問題になる。
正解は
なので,二つの解は
である。したがって,最初の例と同じように
と置いてしまうと![]() が求められないのは当然である。一応演算してみると
が求められないのは当然である。一応演算してみると
となるので,![]() ,
, ![]() と求められる。
これは
と求められる。
これは![]() に他ならないが,
に他ならないが,![]() は求められない。
は求められない。![]() が
最も重要な項であるにもかかわらず,このような単純な摂動では,
それ,つまり最も重要な項が
他の項に比べて無視できるほど小さいとしてしまったことになり,
失敗したと考えられる。
が
最も重要な項であるにもかかわらず,このような単純な摂動では,
それ,つまり最も重要な項が
他の項に比べて無視できるほど小さいとしてしまったことになり,
失敗したと考えられる。
そこでスケールの変更が必要になる。
例えば,方程式の第1項`![]() 'と第3項`1'が
同じくらいの重要なスケールになって,第2項`
'と第3項`1'が
同じくらいの重要なスケールになって,第2項`![]() 'は
無視できるようになると仮定すると,
'は
無視できるようになると仮定すると,![]() のとき
のとき
となって,![]() が他の2項に比べて無視できるとした仮定と矛盾する。
そこで,方程式の第1項`
が他の2項に比べて無視できるとした仮定と矛盾する。
そこで,方程式の第1項`![]() 'と第2項`
'と第2項`![]() 'が
同じくらいの重要なスケールになると仮定すると
'が
同じくらいの重要なスケールになると仮定すると
となるので,第3項の`1'は他の2項に比べて無視できることが確認でき,
スケールの仮定に矛盾が無い。したがって,
![]() ,
つまり
,
つまり
![]() 程度と考えればいいことになる。
結局,新しい座標10.13を
程度と考えればいいことになる。
結局,新しい座標10.13を
と定義し直(スケールの変更を)して,元の方程式を書き直すと
となる。この解を通常の漸近展開で
とした上で方程式に代入して整理すると,まず![]() から
から
を得,![]() から
から
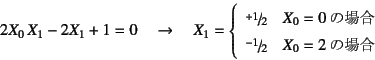
を得る。これは
となり,それぞれが二つの正解![]() ,
, ![]() と一致する。
このようなスケールの変更が必要になる摂動法を特異摂動法
と呼んでいる。
と一致する。
このようなスケールの変更が必要になる摂動法を特異摂動法
と呼んでいる。
さて,振り子運動の非線形微分方程式に戻って,
その解を摂動法によって定量評価をするための一例として,
初期位置の![]() が非線形性に直結する重要なパラメータであると考えよう。
そこで
が非線形性に直結する重要なパラメータであると考えよう。
そこで
という無次元化をしておく。こうすると,運動方程式と初期条件は
と表すことができる。
ただし,この節での上付きドットは![]() による微分を表す。
摂動法を用い易くするために,sine関数をTaylor展開し,
また簡単のために初速は
による微分を表す。
摂動法を用い易くするために,sine関数をTaylor展開し,
また簡単のために初速は![]() とし,解くべき式を
とし,解くべき式を
としておく。
まず,代数方程式を解いたときと同様に,![]() の漸近展開で解を表しておこう。
ここには
の漸近展開で解を表しておこう。
ここには![]() の偶数乗しか存在しないから
の偶数乗しか存在しないから
と置いてもいいだろう。これを微分方程式に代入して![]() のべき乗で整理すると
のべき乗で整理すると
となり,初期条件は
となる。順にべき乗毎に支配方程式を求めると,![]() は
は
となるので,一般解は
![]() で,
初期条件から
で,
初期条件から![]() ,
, ![]() になるので,
になるので,
![]() が解である。
が解である。
では,次のべき乗の![]() の支配方程式を求めると
の支配方程式を求めると
となる。微分方程式の右辺に,上で求められた![]() を代入すると
を代入すると
なので,一般解は
と求められる。これを初期条件に代入すると![]() ,
,
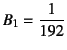 になり
になり
を得る。結局,ここまでのべき乗項で,解は
と求められたことになる。うまくいっているように見えるが,
実は解の![]() の係数の中には
の係数の中には![]() に比例した
項が存在することから,これは発散解になっていることがわかる。
つまり,どんなに初期位置の
に比例した
項が存在することから,これは発散解になっていることがわかる。
つまり,どんなに初期位置の![]() が
小さくても,振り子のような振動解ではなく,時間とともに
回転角が大きくなるという解しか求められなかったことになり,
これは前節の位相平面上の定性的な検討結果とも矛盾する。
すなわち,このアプローチは失敗なのである。
が
小さくても,振り子のような振動解ではなく,時間とともに
回転角が大きくなるという解しか求められなかったことになり,
これは前節の位相平面上の定性的な検討結果とも矛盾する。
すなわち,このアプローチは失敗なのである。
何がまずかったのか。実は,上のアプローチでは,振動数が![]() の
解を求めようとしていた。この振動数が
の
解を求めようとしていた。この振動数が![]() とは無関係の一定値であると
していた。もしかしたら,そこがまずかったのではないか(と,賢い人が
考えたのである)。
そこで,
とは無関係の一定値であると
していた。もしかしたら,そこがまずかったのではないか(と,賢い人が
考えたのである)。
そこで,![]() ではなく,
ではなく,![]() に依存した振動数
に依存した振動数
![]() で
揺れる運動の解を探してみることにする。ここに
で
揺れる運動の解を探してみることにする。ここに![]() は未知の
関数である。そこで
は未知の
関数である。そこで
という独立変数10.14を導入し,![]() ではなく
ではなく![]() に関する
に関する![]() 周期の
解を探すことにしよう。この変数変換から
周期の
解を探すことにしよう。この変数変換から
とすればいいので,基礎式(10.261)は
となる。ここのプライムは![]() による微分を表す。ここで,漸近展開を
による微分を表す。ここで,漸近展開を
のように置くことにする。![]() も展開していることに注意する。
も展開していることに注意する。
これから
であることに留意して,上の基礎方程式に代入して整理する。
まず![]() の項を集めると
の項を集めると
と求められる。したがって,一般解を求めて初期条件に代入すると,
結局解は
と求められる。ここでは周期解,特に![]() については
については![]() 周期の
解を探していることから,
周期の
解を探していることから,
![]() は自然数でなければならない。
特に微小振動の解は
は自然数でなければならない。
特に微小振動の解は![]() の解に相当することから,
ここではそれが答だとする。したがって
の解に相当することから,
ここではそれが答だとする。したがって
という解を得る。
次に,素朴なアプローチでは失敗した![]() の項を検討しよう。
このべき乗の項を集めると
の項を検討しよう。
このべき乗の項を集めると
という微分方程式を得る。初期条件を陽な形で示すのは難しいの割愛する。
この式の両辺に,![]() の計算で得た結果の式(10.264)を
代入すると,結局
の計算で得た結果の式(10.264)を
代入すると,結局
という微分方程式になる。素朴なアプローチで発散解を発生させた
非斉次項は![]() の項である。これが存在する限り,発散解が特解として
存在することになる。つまり,この項が無くなれば周期解を得ることができる。
上式の
の項である。これが存在する限り,発散解が特解として
存在することになる。つまり,この項が無くなれば周期解を得ることができる。
上式の![]() の項を消すためには
の項を消すためには
であればいいことになる。そのとき一般解は
と求められる。
ここまでの解を集めると
と表すことができる。これは周期解であるが,振動数も
初期位置![]() に依存した値になっている。この解を,例えば
に依存した値になっている。この解を,例えば
と置くと,それは,微小振動(線形系近似)のときの振動数が若干改善されて
| (10.264) |
としたことになる。これをPoincaréの周波数シフト
と呼ぶ。あるいは
| (10.265) |
と解釈したとすると,それは,時刻という独立変数(座標)を初期位置によって
若干伸び縮みさせたもの,つまりスケール変更したものが
のように定義されたと考えてもいい。 こういった考え方をmethod of strained coordinates と呼ぶことがある。 この考え方は,ミクロ・マクロのマルチスケール解析法の 一つである均質化法[113] の根拠にもなっている。 この振り子の問題のときは,`method of strained coordinates'と「Poincaréの 周波数シフト」による解が一致するが,一般には必ずしもそうではないらしい。
振り子が初速零で初期位置![]() から
運動を始めると,図-10.65の
太線のような位相平面上の軌跡を描く。
ちょうど逆立ちした状態
から
運動を始めると,図-10.65の
太線のような位相平面上の軌跡を描く。
ちょうど逆立ちした状態![]() は分岐点のようなもので,
その状態で逆転して元の方向に戻る運動の可能性と,そのまま同じ方向に
回転し続けようとする運動の可能性の二つが存在する。
位相平面上の軌跡は,
は分岐点のようなもので,
その状態で逆転して元の方向に戻る運動の可能性と,そのまま同じ方向に
回転し続けようとする運動の可能性の二つが存在する。
位相平面上の軌跡は,![]() で角が発生しているのは興味深い。
いずれにしても逆立ち状態は不安定である。
しかし,その状態は式(10.255)で加速度が零の場合の式から
で角が発生しているのは興味深い。
いずれにしても逆立ち状態は不安定である。
しかし,その状態は式(10.255)で加速度が零の場合の式から
が解であることから,明らかに静的なつり合い状態である。
そこで,静的なつり合い状態が安定か不安定かの判断をするために,
動的な挙動を利用することを考えてみよう。
この手法は,剛体バネモデルの座屈を調べた節-6.2.1
(3)でも用いた。代表的な静的つり合い状態
として
![]() と
と
![]() の二つを対象とする。
このつり合い状態からの微小な乱れを
の二つを対象とする。
このつり合い状態からの微小な乱れを![]() と記すことにすると
と記すことにすると
としていいから,
これを運動方程式(10.255)に代入すれば,![]() に
ついて線形化できるので
に
ついて線形化できるので
を得る。したがって,ここで選んだ二つの静的つり合い状態は,それぞれ
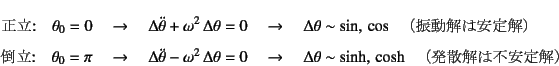
というように微小な乱れが求められる。正立の![]() に
対する乱れは周期解であり,
静的つり合い位置を中心とした振り子運動をするので,
もし減衰が存在すればそのうち止まることを示している。
つまり安定な状態であると判定できる。
一方,逆立ち状態の解は双曲線関数あるいは指数関数であり,発散解である。
したがって逆立ち状態は不安定であると判定できる。
に
対する乱れは周期解であり,
静的つり合い位置を中心とした振り子運動をするので,
もし減衰が存在すればそのうち止まることを示している。
つまり安定な状態であると判定できる。
一方,逆立ち状態の解は双曲線関数あるいは指数関数であり,発散解である。
したがって逆立ち状態は不安定であると判定できる。
粘性減衰振動モデルで,減衰定数が負の場合には発散する。
風荷重を受ける橋梁等では,このような動的不安定が発生すると考えられている。
似たようなもので,電気回路の振動例に一つ面白いものがある。
それはvan der Pol振動子
と呼ばれるもので,ある![]() に対して
に対して
という支配方程式でモデル化されている。容易に予想できるように,![]() で
あれば正の減衰であり,その逆なら負減衰なので発散しようとする。
だから,振幅が大きくなると減衰が働き,小さい振幅になると
発散しようとする。したがってこのモデルは,
発散解も減衰解も,ある周期解に収束しようとすることが予想される。
その収束する先の周期解をリミットサイクルと呼んでいる。
この問題も摂動法で解いてみるが,リミットサイクルを求める程度なら
素朴なアプローチで十分なことがわかっている。
で
あれば正の減衰であり,その逆なら負減衰なので発散しようとする。
だから,振幅が大きくなると減衰が働き,小さい振幅になると
発散しようとする。したがってこのモデルは,
発散解も減衰解も,ある周期解に収束しようとすることが予想される。
その収束する先の周期解をリミットサイクルと呼んでいる。
この問題も摂動法で解いてみるが,リミットサイクルを求める程度なら
素朴なアプローチで十分なことがわかっている。
まず解を
と置き,式(10.267)に代入して整理すると
と,初期条件が
になる。これより,まず![]() の項は
の項は
となるので,解は
と求められる。次に![]() の項は
の項は
となる。これに上の![]() を代入すると,
を代入すると,![]() の特解
の特解
![]() として
として
を得る。右辺の第1項は,前節の振り子の問題と同じく発散解である。
今求めようとしているのは,リミットサイクルという周期解なので,
この項は零になる必要がある。したがって![]() だから
だから
でなければならない。つまり,リミットサイクルは初期条件が![]() の
振動解になる。したがって一般解は
の
振動解になる。したがって一般解は
と求められ,初期条件から![]() ,
,
![]() となるので
となるので
を得る。以上の摂動解の範囲で
と求められる。![]() を媒介変数とすれば位相平面上のリミットサイクルを
描くことができ,図-10.66にはそれを実線で示した。
これは,上で求められた
を媒介変数とすれば位相平面上のリミットサイクルを
描くことができ,図-10.66にはそれを実線で示した。
これは,上で求められた![]() と
と![]() を,
を,![]() までの
範囲で描いたものである。これに対し破線と一点鎖線は,
減衰定数を
までの
範囲で描いたものである。これに対し破線と一点鎖線は,
減衰定数を
と置いた上で,中央差分で数値的に求めたものである。
破線は![]() の初期条件から,
一点鎖線は
の初期条件から,
一点鎖線は![]() の初期条件から始めたものである。
実線は
の初期条件から始めたものである。
実線は![]() までの摂動解なので,数値解のたどり着く先とは若干の
ずれがある。しかし,発散解も減衰解もある周期解に
収束しようとしていることが明らかである。
数値解析によって,容易に非線形解析もできることも楽しいでしょ。
までの摂動解なので,数値解のたどり着く先とは若干の
ずれがある。しかし,発散解も減衰解もある周期解に
収束しようとしていることが明らかである。
数値解析によって,容易に非線形解析もできることも楽しいでしょ。
図-10.67の左側には,長さ![]() の振り子の
支点が上下に
の振り子の
支点が上下に![]() で強制的に変位させられ,それに伴って
左右に振動している状態を描いてある。しかし,これはおかしくないか。
本当に左右に振動するだろうか。
手で実験するのはかなり難しいが,乱れが生じないように
そぉーっとゆっくり振り子の支点を上下させても,
それがその運動の直角方向に振り子運動を始めるとは予想し難い。
右側の図には,同じ振り子が天井の穴を
通して設置された上で,支点を上下に
で強制的に変位させられ,それに伴って
左右に振動している状態を描いてある。しかし,これはおかしくないか。
本当に左右に振動するだろうか。
手で実験するのはかなり難しいが,乱れが生じないように
そぉーっとゆっくり振り子の支点を上下させても,
それがその運動の直角方向に振り子運動を始めるとは予想し難い。
右側の図には,同じ振り子が天井の穴を
通して設置された上で,支点を上下に![]() で強制的に変位させた
ため,振り子そのものの長さが元の長さではなく
で強制的に変位させた
ため,振り子そのものの長さが元の長さではなく![]() に
なりながら振動している状態を描いた。
このような振り子を変調振り子
と呼んでいる。社会基盤構造の場合,
例えば吊橋や斜張橋のケーブルがその張られている面内で
上下左右に振動をしているとき,場合によってはその面外に振動を
始める現象[104]が,この変調振り子と同じものと考えられている。
に
なりながら振動している状態を描いた。
このような振り子を変調振り子
と呼んでいる。社会基盤構造の場合,
例えば吊橋や斜張橋のケーブルがその張られている面内で
上下左右に振動をしているとき,場合によってはその面外に振動を
始める現象[104]が,この変調振り子と同じものと考えられている。
まず左側の図のような運動の場合,質点の変位は
であるから,加速度は
となる。一方,糸の張力を![]() とすると,左右上下方向の運動方程式はそれぞれ
とすると,左右上下方向の運動方程式はそれぞれ
となるので,![]() を消去すれば
を消去すれば
と表される。この式(![]() )に式(
)に式(![]() )を
代入して整理すると
)を
代入して整理すると
のように運動方程式が求められる。ここで,支点の強制変位はcosine関数で
与えられるとして
と定義すると,上式は
となる。もし微小な振動を考えるとすれば,sine関数を近似して
図-10.67の右側の図に示した振り子の場合は
となっているので,加速度が
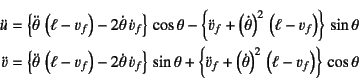
と表される。運動方程式は式(![]() )と同じなので,
それに代入して整理すると
)と同じなので,
それに代入して整理すると
となる。ここで
![]() と定義して
上式に代入すると
と定義して
上式に代入すると
と表すことができる。さらに,変位は大きくなく,近似的に
が成立するものとして,前の例と同様に,
式(10.268)で強制変位が与えられているとすると,上式は
となる。これも式(10.269)と同じMathieu方程式である。
ここで変数変換をして
とし,
![]() と置き換えると,上式は
と置き換えると,上式は
と変形できる。ここの上付きドットは![]() による微分である。そこで
による微分である。そこで
と定義すると,最終的にMathieu方程式は
と表すことができる。
最初は単純な摂動法を用いてみる。
と置いて,上式(10.271)に代入して整理すると
となる。これから![]() のレベルの解は
のレベルの解は
となる。ただし,![]() 周期の解でなければならないので
周期の解でなければならないので
と求められる。
次に![]() のレベルの方程式は
のレベルの方程式は
となる。まず![]() の場合には
の場合には
のように周期解が求められるので,特に問題は生じない。しかし![]() の場合の
運動方程式は
の場合の
運動方程式は
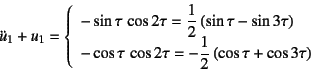
となるので,右辺の![]() ,
, ![]() の項に対応して,
特解には必ず
の項に対応して,
特解には必ず
![]() ,
,
![]() の項が存在し,
発散解にしかならない。
つまり,この運動は不安定である可能性があり,
確かに実験では不安定な運動になる。
の項が存在し,
発散解にしかならない。
つまり,この運動は不安定である可能性があり,
確かに実験では不安定な運動になる。
そこで,特異摂動法を用いて,周期解を探してみる。
そのために,式(10.272)の摂動に加えて,![]() が
が![]() に
依存するものとして
に
依存するものとして
という漸近展開をしておく。これを方程式(10.271)に代入して
整理すると
となる。これから![]() のレベルの解は,素朴なアプローチと同じで
のレベルの解は,素朴なアプローチと同じで
と求められる。
では![]() ,
, ![]() の場合をまず考えてみる。
の場合をまず考えてみる。![]() のレベルの方程式は
のレベルの方程式は
となるので,解は
と求められる。周期解になるためには
でなければならないので,解は
と求められる。次に![]() のレベルの運動方程式は
のレベルの運動方程式は
となるので,再度発散解にならない条件から
と求められる。ここまでの漸近展開では,![]() が
が
でないと,周期解が存在しないことがわかる。
次に![]() の場合を考えよう。
の場合を考えよう。![]() ,
, ![]() の
場合の
の
場合の![]() のレベルの運動方程式は
のレベルの運動方程式は
となるので,周期解を得るには
でいいこと(斉次解はあっても無くても一緒)になる。
次に![]() のレベルが
のレベルが
となる。したがって,周期解を得るには
![]() で
あればいいから,結局,ここまでの漸近展開では,
で
あればいいから,結局,ここまでの漸近展開では,![]() が
が
でないと,周期解が存在しないことがわかる。
同様の演算を![]() で
で![]() ,
, ![]() の
場合で実行する。
の
場合で実行する。![]() のレベルの運動方程式は
のレベルの運動方程式は
となるので,周期解を得るには
でいいことになる。次に![]() のレベルが
のレベルが
となる。したがって,周期解を得るには
![]() で
あればいいから,結局,ここまでの漸近展開では,
で
あればいいから,結局,ここまでの漸近展開では,![]() が
が
でないと,周期解が存在しないことがわかる。
同様の演算を![]() ,
,
![]() ,
,
![]() に対して
行うと,結局
に対して
行うと,結局
![]() に対しては
に対しては
と求められる。また
![]() に対しては
に対しては
でないといけないことがわかる。
以上の式(![]() )〜(
)〜(![]() )の関係式を
描いたのが図-10.68の左の図である。
この線上であれば解は振動解であることがわかった。
そこで,
)の関係式を
描いたのが図-10.68の左の図である。
この線上であれば解は振動解であることがわかった。
そこで,![]() として,式(
として,式(![]() ) (
) (![]() )で
挟まれたくさびの中に相当する
)で
挟まれたくさびの中に相当する![]() の場合と,
くさびの外に相当する
の場合と,
くさびの外に相当する![]() の場合について,
中央差分法を用いてMathieu方程式を解いてみた。
その解が図-10.68の右の図である。
くさびの外の設定の解(細い実線)は振動解を示していて,
安定な解であることがわかる。くさびの中の設定(太い実線)の場合には,
解はかなり速く振幅が大きくなり,発散解であることを示唆している。
二つの解の周期も異なることに注意する。
このことから,図-10.68の左の図に示したように,
動的応答が安定解である
の場合について,
中央差分法を用いてMathieu方程式を解いてみた。
その解が図-10.68の右の図である。
くさびの外の設定の解(細い実線)は振動解を示していて,
安定な解であることがわかる。くさびの中の設定(太い実線)の場合には,
解はかなり速く振幅が大きくなり,発散解であることを示唆している。
二つの解の周期も異なることに注意する。
このことから,図-10.68の左の図に示したように,
動的応答が安定解である
![]() の組み合わせと,
不安定な発散解である場合が存在する。
ここでは数値的な解で安定性を確認してみたが,
数学的にはFloquetの定理を用いて,図示したような安定領域を
決定することができる。
の組み合わせと,
不安定な発散解である場合が存在する。
ここでは数値的な解で安定性を確認してみたが,
数学的にはFloquetの定理を用いて,図示したような安定領域を
決定することができる。
Floquet Theorem: 周期の係数を持つ線形常微分方程式の解は
で表される。ここには周期が
で,
は定数で 実数とは限らない。
の符号で,解が発散解か 減衰解かの判断ができる。
実際には![]() が零の周辺で摂動を考え
が零の周辺で摂動を考え
と置いて,Mathieu方程式を解く。例えば![]() の場合,
くさびの中の設定では
の場合,
くさびの中の設定では![]() が実数になり発散解であることを意味し,
くさびの上では
が実数になり発散解であることを意味し,
くさびの上では![]() なので周期解を意味し,
くさびの外の設定では
なので周期解を意味し,
くさびの外の設定では![]() は純虚数になって,若干の周波数シフトを
伴った振動解になることを示すことができるそうだ。
このような動的不安定現象を係数励振
と呼んでいるが,実はこれはブランコ
がこげる原理なのである。図-10.67の右の
変調振り子は,見方を変えると,振り子の重りの重心が上下運動したときの
運動と同じである。つまり,ブランコに乗った幼稚園児が足を屈伸して
その重心を上下させることによって,ブランコが揺れ始めるのと同じである。
幼稚園児が,体でMathieu方程式を解くことができるというのは興味深い。
その園児が大学生になると線形の常微分方程式も解けなくなるのだから。
この現象には,1980年代にNorthwestern大学のTechnological Instituteの
オープンキャンパスで,機械工学科の学生が見せてくれた模型で
初めて接した。そのときのオープンキャンパスでは,この係数励振の模型と
箱庭地盤の液状化模型には感激した。二つの類似模型は,
東北大学工学部土木工学科の元技術職員の菅原紘一さんに作ってもらって,
何回かオープンキャンパスでも見せることができた。
は純虚数になって,若干の周波数シフトを
伴った振動解になることを示すことができるそうだ。
このような動的不安定現象を係数励振
と呼んでいるが,実はこれはブランコ
がこげる原理なのである。図-10.67の右の
変調振り子は,見方を変えると,振り子の重りの重心が上下運動したときの
運動と同じである。つまり,ブランコに乗った幼稚園児が足を屈伸して
その重心を上下させることによって,ブランコが揺れ始めるのと同じである。
幼稚園児が,体でMathieu方程式を解くことができるというのは興味深い。
その園児が大学生になると線形の常微分方程式も解けなくなるのだから。
この現象には,1980年代にNorthwestern大学のTechnological Instituteの
オープンキャンパスで,機械工学科の学生が見せてくれた模型で
初めて接した。そのときのオープンキャンパスでは,この係数励振の模型と
箱庭地盤の液状化模型には感激した。二つの類似模型は,
東北大学工学部土木工学科の元技術職員の菅原紘一さんに作ってもらって,
何回かオープンキャンパスでも見せることができた。
社会基盤構造の場合,材料の非線形性の代表で重要なものは塑性である。
しかしながら,塑性理論は複雑で,特に除荷と載荷の変形経路が
異なることによって,動的解析に正確に組み込むことが
困難なことが多い。ここでは,もう少し簡単な非線形弾性体のような
ものを対象としてみる。図-10.69に示したように,
例えばバネの抵抗力![]() がバネの伸び
がバネの伸び![]() との間に
との間に
のような法則が成立する場合を考えよう。![]() が
線形バネの弾性係数であり,
が
線形バネの弾性係数であり,![]() が非線形性を代表する弾性係数で,
正の場合は硬化材料であり,負の場合は軟化材料のモデルに相当する。
が非線形性を代表する弾性係数で,
正の場合は硬化材料であり,負の場合は軟化材料のモデルに相当する。
このような抵抗則の線形バネに![]() の外力が作用した場合の,
共振点付近の振動を解析したい。対応する運動方程式は
の外力が作用した場合の,
共振点付近の振動を解析したい。対応する運動方程式は
と表される。初期条件は零初期条件としておく。
このような振動モデルをDuffingの振動子
と呼んでいる。この問題も摂動法を用いて解いてみよう。
と置き,式(10.275)に代入して整理すると
となる。![]() のレベルからは,1自由度系の強制振動の解と同じで
のレベルからは,1自由度系の強制振動の解と同じで
が特解になる。上述のようにここでは,この分母が非常に小さい場合,
つまり共振点付近の非線形応答を求めたい。
しかし,このまま続けて![]() のレベルに代入したとしても,
分母は
のレベルに代入したとしても,
分母は
![]() のべき乗の乗数が大きくなる
だけで,さらに問題が重大になるだけである。
のべき乗の乗数が大きくなる
だけで,さらに問題が重大になるだけである。
そこで,外力レベルは小さいものとすれば,共振点付近の挙動が
求められるかもしれないと考え,当面は
と置いた上で,時刻を外力周波数で無次元化して
と定義する。以下,上付きドットは![]() による微分を表すものとする。
上の運動方程式(10.275)を書き直すと
による微分を表すものとする。
上の運動方程式(10.275)を書き直すと
となる。そこで![]() が共振点
が共振点![]() に近い場合を対象とすることから,
摂動展開を
に近い場合を対象とすることから,
摂動展開を
とすると,![]() は
は
と表される。この展開を運動方程式に代入すると,まず![]() のレベルは
のレベルは
となるので,一般解は
でいい。次に![]() のレベルは
のレベルは
となる。
これに上の![]() を代入して整理すると,右辺には
問題を発生させる
を代入して整理すると,右辺には
問題を発生させる![]() ,
, ![]() の他に,
の他に,![]() ,
, ![]() の
項が存在する。周期解を得るためには,前2者は無くなって欲しいわけである。
そこでその二つの項を集めると
の
項が存在する。周期解を得るためには,前2者は無くなって欲しいわけである。
そこでその二つの項を集めると
と求められる。この各係数がいずれも零になって
が成立すれば周期解を得ることができる。この第1式の括弧が零であれば,
第2式から![]() という意味の無い解しか求められないので,
結局第1式から
という意味の無い解しか求められないので,
結局第1式から![]() でなければならない。したがって,第2式に代入して
でなければならない。したがって,第2式に代入して
という関係が成立しなければならない。式(![]() )の
)の![]() の定義と
式(
の定義と
式(![]() )の摂動展開の表現をそれぞれ,この第3, 1項に代入すると結局
)の摂動展開の表現をそれぞれ,この第3, 1項に代入すると結局
となることから,非線形の材料パラメータ
![]() を含んだ
振幅
を含んだ
振幅![]() を求める式が
を求める式が
のように求め10.15られる。
図-10.70には,
縦軸に
![]() つまり
つまり
![]() をとり,
非線形系の場合の共振曲線を描いた。パラメータは,
をとり,
非線形系の場合の共振曲線を描いた。パラメータは,![]() ,
, ![]() とした上で,
硬化の場合は
とした上で,
硬化の場合は
![]() とした結果であり,
軟化の場合は
とした結果であり,
軟化の場合は
![]() とした
結果である。
とした
結果である。
![]() 付近でも有界の振幅を得る等,
線形系の共振曲線とは異なる特徴が明らかである。
特に,破線で示した振幅の振動は不安定であり,現実には生じ得ない。
したがって,共振点付近での挙動は複雑なものになることが予想される。
付近でも有界の振幅を得る等,
線形系の共振曲線とは異なる特徴が明らかである。
特に,破線で示した振幅の振動は不安定であり,現実には生じ得ない。
したがって,共振点付近での挙動は複雑なものになることが予想される。
そこで,再度中央差分を用いた数値解析アプローチで,時系列挙動を
求めてみた。図-10.71は,![]() ,
, ![]() として,
硬化の場合は
として,
硬化の場合は![]() ,
,
![]() とした結果であり,
軟化の場合は
とした結果であり,
軟化の場合は![]() ,
,
![]() とした結果である。
それぞれの図の下には,位相平面上の挙動も示してある。
時系列応答はそれほど複雑ではないが,位相平面上の軌跡は面白い。
もう少し複雑な挙動を探して,いろいろなパラメータの値を試してみたが,
例えば図-10.72には
とした結果である。
それぞれの図の下には,位相平面上の挙動も示してある。
時系列応答はそれほど複雑ではないが,位相平面上の軌跡は面白い。
もう少し複雑な挙動を探して,いろいろなパラメータの値を試してみたが,
例えば図-10.72には![]() をもう少し
大きくした場合の結果を示した。例では
をもう少し
大きくした場合の結果を示した。例では![]() ,
, ![]() ,
, ![]() としている。
この挙動は複雑に見えるが,
時系列応答はさほど変わったものにはなってはいない。
各自,いろいろ試してみるといい。
このようなアプローチは,動的不安定現象にはよく用いられているようだ。
変わったところでは,心理学の分野にも力学モデルとして適用しているような
情報を,インターネットで見たことがある。
としている。
この挙動は複雑に見えるが,
時系列応答はさほど変わったものにはなってはいない。
各自,いろいろ試してみるといい。
このようなアプローチは,動的不安定現象にはよく用いられているようだ。
変わったところでは,心理学の分野にも力学モデルとして適用しているような
情報を,インターネットで見たことがある。
特にDuffingの振動子の場合には,![]() によるスケールの変更を
随所で用いている。これは摂動法の使い方がとても難しいことを示唆している。
例えば,1自由度系の線形の粘性減衰自由振動の問題に戻ろう。
減衰定数に相当するパラメータを
によるスケールの変更を
随所で用いている。これは摂動法の使い方がとても難しいことを示唆している。
例えば,1自由度系の線形の粘性減衰自由振動の問題に戻ろう。
減衰定数に相当するパラメータを![]() とすると,運動方程式は
とすると,運動方程式は
となる。初期条件を
として,これを摂動法で解いてみる。もちろん,素朴なアプローチは
破綻するだろうと予想して,method of strained coordinatesを用い
と置いておく。以下の演算を実施すると,すぐ![]() のレベルで
のレベルで
を得る。ここにプライムは![]() による微分である。ここで既に右辺の
不要な項を消すような
による微分である。ここで既に右辺の
不要な項を消すような![]() が存在しなくなり,破綻してしまっている。
が存在しなくなり,破綻してしまっている。
これはなぜか。もちろんすべての読者は既に減衰自由振動の正解を
知っているはずだが,その解は
である。この指数関数のところとsine関数のところの時刻![]() は,
それぞれ異なる速さでシフトしないといけない変数になっている。
したがって,1種類のstrained coordinateでは摂動解は求められないことになる。
これを克服するために,「速い時刻」と「遅い時刻」の二つの
時刻スケールを導入して摂動解析する方法が提案されており,
それはmethod of multiple scales
と呼ばれている。
これ以上は理解していないので,ここいらでやめる。
は,
それぞれ異なる速さでシフトしないといけない変数になっている。
したがって,1種類のstrained coordinateでは摂動解は求められないことになる。
これを克服するために,「速い時刻」と「遅い時刻」の二つの
時刻スケールを導入して摂動解析する方法が提案されており,
それはmethod of multiple scales
と呼ばれている。
これ以上は理解していないので,ここいらでやめる。