 |
�ŐV�ł𐳊m�ɓǂޏꍇ�ɂ� pdf �t�@�C�� ���ǂ����B����� web �����̂��߂̊ȈՋ��łł��B
���̏͂́C������w�̈ɓ��w���_������1970�N���� �u�`�m�[�g�����ɂ����B�����̋��ȏ��͕���[97]�ł��������C �������ɂȂ����͕̂���[87]�̕����Ǝv����B�܂�1���R�x�n�� �U������p���āC�U���_�ɂ����čł��d�v�ȌŗL�U������ ���U�Ƃ����T�O���������B�����R�x�n�̏ꍇ�ɂ́C����� �x�N�g���Ƃ��Ă̌ŗL�U�����[�h�Ƃ����T�O�����C��������B �����ė����Ƃ����A���̂̐U���̏ꍇ�ɂ́C���̌ŗL�U�����[�h�� ���ɂȂ��Ă��邱�Ƃ��������B�ŏI�I�ɂ� �L���v�f�@��p���邱�Ƃɂ���āC�A���̂͌������㑽���R�x�n�Ƃ��� �ߎ��I�Ɏ�舵�����Ƃ��ł��邱�Ƃ��������B�������C���U�� ���g���������̓����C����ɋ��E�����ɂ���ă��[�h���ς�邱�Ɠ����C ���l��͂�����܂ł��Ȃ��\�z�ł���悤�ȋZ�p�҂ɂȂ��ė~�����B ���l��͂́C�P�Ȃ�c�[���ł����Ȃ��C�Z�p�҂̗͊w�I�����̕����d�v�ł���B �Ȃ��C���̕����ł͒e���͈݂͂̂�ΏۂƂ���̂ŁC���x�v�̂��߂ɂ� ����Ȃ�w�K���K�v�ł���B
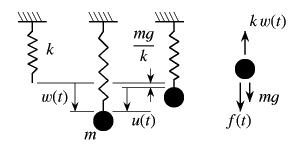
�Ⴆ�C�o�l�萔![]() �̐��`�o�l�Ɏ��t����1�̎��_�̉^�����l���悤�B
�o�l�̎��ʂ͖����ł�����̂���B�}-10.1�̂悤�ɁC
���R��Ԃ̃o�l�̐�[�Ɏ���
�̐��`�o�l�Ɏ��t����1�̎��_�̉^�����l���悤�B
�o�l�̎��ʂ͖����ł�����̂���B�}-10.1�̂悤�ɁC
���R��Ԃ̃o�l�̐�[�Ɏ���![]() �̎��_��t�����Ƃ���^�����n�߂��B
���̂Ƃ��̎��_�̉����ւ̕ψʁi�o�l�̐L�сj��
�̎��_��t�����Ƃ���^�����n�߂��B
���̂Ƃ��̎��_�̉����ւ̕ψʁi�o�l�̐L�сj��![]() �Ƃ��C
���_�ɂ͊O��
�Ƃ��C
���_�ɂ͊O��![]() ����p���邱�Ƃ��ł�����̂Ƃ���B
���̂Ƃ��C���_�̉^�������i�}�ł͉����j�ɍ�p���Ă���͂�
���a�́C�}�̉E�[�ɂ���͂̃_�C�A�O��������
����p���邱�Ƃ��ł�����̂Ƃ���B
���̂Ƃ��C���_�̉^�������i�}�ł͉����j�ɍ�p���Ă���͂�
���a�́C�}�̉E�[�ɂ���͂̃_�C�A�O��������
�ł���B����������Newton�̖@���i
![]() �j����C�^����������
�j����C�^����������
| (10.1) |
�ƂȂ�B�ȉ��C��t���h�b�g�͎��Ԃɂ�������\���B
����![]() �̑����
�̑����
| (10.2) |
��p����ƁC
![]() �Ȃ̂ŁC�^��������(10.1)��
�Ȃ̂ŁC�^��������(10.1)��
| (10.3) |
�ƂȂ�B
���̎�(10.2)��![]() �́C�}-10.1��
������O�Ԗڂ̐}�Ɏ������悤�ɁC���_���o�l�ɂ����[���Ǝ��t��������
�ÓI�ɂ荇������Ԃ���̕ψʂł���B
���̌`�̕������́C���̃o�l���_�n�����C�̖������̏�Ő�����
�U������ꍇ�̎��Ɉ�v����B�܂��C�Љ��Ս\����
�U�����ł́C���ɂ荇���Ă����Ԃ���̓��I�ȕϓ��ɋ�����
���邱�Ƃ̕��������̂ŁC�Ȍ�C�����Ƃ��Ď��d�i���d�j�̍��͖������āC
��(10.3)��W���I�ȉ^���������Ƃ���B
�����ŊO��
�́C�}-10.1��
������O�Ԗڂ̐}�Ɏ������悤�ɁC���_���o�l�ɂ����[���Ǝ��t��������
�ÓI�ɂ荇������Ԃ���̕ψʂł���B
���̌`�̕������́C���̃o�l���_�n�����C�̖������̏�Ő�����
�U������ꍇ�̎��Ɉ�v����B�܂��C�Љ��Ս\����
�U�����ł́C���ɂ荇���Ă����Ԃ���̓��I�ȕϓ��ɋ�����
���邱�Ƃ̕��������̂ŁC�Ȍ�C�����Ƃ��Ď��d�i���d�j�̍��͖������āC
��(10.3)��W���I�ȉ^���������Ƃ���B
�����ŊO��![]() ����p���Ă��Ȃ��U���̂��Ƃ����R�U��
�ƌĂ�ł���B
�ߑ�ڂɂ���u���v�ɂ��Ă͍��͂킩��Ȃ��Ă����B
����p���Ă��Ȃ��U���̂��Ƃ����R�U��
�ƌĂ�ł���B
�ߑ�ڂɂ���u���v�ɂ��Ă͍��͂킩��Ȃ��Ă����B
��̗�͎��_�̕��i�^����ΏۂƂ����B���ɐU��q�^�����l���Ă݂悤�B
�U��q�͏d�͏�ł̉^���Ȃ̂ŏd�͉����x![]() ���l�����邱�Ƃɂ���B
��]�^���ɂ��Ă�Newton�̖@���́C�^���̉�]�p��
���l�����邱�Ƃɂ���B
��]�^���ɂ��Ă�Newton�̖@���́C�^���̉�]�p��![]() �Ƃ����Ƃ��C
���̉�]�p�̌����ɍ�p���Ă���O�̓��[�����g�̑��a��
�Ƃ����Ƃ��C
���̉�]�p�̌����ɍ�p���Ă���O�̓��[�����g�̑��a��![]() �Ƃ����
�Ƃ����
| (10.4) |
�ł���B������![]() ���������[�����g
�ƌĂ�
���������[�����g
�ƌĂ�
| (10.5) |
�Œ�`�����B������![]() �͖��x�ŁC
�͖��x�ŁC![]() �͉�]���S�����
�����C
�͉�]���S�����
�����C![]() �͑̐ςł���B
����͕��i�^���̎���
�͑̐ςł���B
����͕��i�^���̎���![]() �̒�`
�̒�`
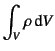 �ɑΉ������C
��]�^���̕����p�����[�^�ł���B
�ɑΉ������C
��]�^���̕����p�����[�^�ł���B
�����Ő}-10.2��
�U��q���l���悤�B�U��q�̎��͎��ʂ������L�яk�݂����Ȃ����̂Ƃ���B
�U��q�̉�]�������v�����![]() ���Ƃ���ƁC
�x�_���ɂ��̐U��q�ɍ�p���Ă��郂�[�����g�͏d�͂�
�e���݂̂ŁC����������v���𐳂Ƃ����
���Ƃ���ƁC
�x�_���ɂ��̐U��q�ɍ�p���Ă��郂�[�����g�͏d�͂�
�e���݂̂ŁC����������v���𐳂Ƃ����
�����ł���B�����ł͗h��̑傫���͏�����
![]() ��
��������Ƌߎ������B���ʂ͐U��q�̐�[�ɂ��������̂ŁC
�������[�����g��
��
��������Ƌߎ������B���ʂ͐U��q�̐�[�ɂ��������̂ŁC
�������[�����g��![]() �ƂȂ�B���������āC��]��
�^��������(10.4)��
�ƂȂ�B���������āC��]��
�^��������(10.4)��
| (10.6) |
�ƂȂ�B������`���I�ɂ́C��(10.3)�̕W���I�ȉ^����������
�����`[(![]() ,
, ![]() )
)
![]() (
(![]() ,
, ![]() )]�ɂȂ��Ă��邱�Ƃ��킩��B
)]�ɂȂ��Ă��邱�Ƃ��킩��B
�ł͎�(10.3)��p���āC�O��![]() ����p���Ă��Ȃ�
��Ԃ̎��R�U�������߂Ă݂悤�B�^����������2�K�̏�����������Ȃ̂ŁC
�B��ȉ��邽�߂ɂ́C����
����p���Ă��Ȃ�
��Ԃ̎��R�U�������߂Ă݂悤�B�^����������2�K�̏�����������Ȃ̂ŁC
�B��ȉ��邽�߂ɂ́C����![]() �ɂ������ԁC
�܂菉��������2���^����K�v������B����́C
�ł��P���Ȑݒ�́C���_�̏����̈ʒu��
�����̑��x�i�ȉ��C�����ƌĂԁj��^���邱�Ƃł���C�Ⴆ��
�ɂ������ԁC
�܂菉��������2���^����K�v������B����́C
�ł��P���Ȑݒ�́C���_�̏����̈ʒu��
�����̑��x�i�ȉ��C�����ƌĂԁj��^���邱�Ƃł���C�Ⴆ��
�Ɨ^�����邱�Ƃɂ��悤�B
��(10.3)��ӁX![]() �Ŋ���C
�Ŋ���C![]() ��
��![]() �����̒萔�ł��邱�Ƃ���
�����̒萔�ł��邱�Ƃ���
�ƒ�`����ƁC�^����������
�ƂȂ�B
���̔����������̈�ʉ������߂邽�߂�
![]() �ƒu���C
�^��������(10.9)�ɑ������ƁC
�ƒu���C
�^��������(10.9)�ɑ������ƁC![]() �ɂ��Ă�
�����������Ƃ��̍���
�ɂ��Ă�
�����������Ƃ��̍���
�Ƌ��߂���B
���������ĉ��́CEuler�̌���(10.62)�i
![]() �j����
�j����
| (10.10) |
�Ƌ��߂���B![]() ���U��
�ƌĂ�Ă���B�ϕ��萔
���U��
�ƌĂ�Ă���B�ϕ��萔![]() ��
��![]() �C���邢��
�C���邢��![]() ��
��![]() ��
����������(10.7)��
����ł���C���ꂪ���ɂȂ�B
��
����������(10.7)��
����ł���C���ꂪ���ɂȂ�B![]() ��
��![]() ���g�������̕\�������������ɑ�������
���g�������̕\�������������ɑ�������
�Ƌ��߂���B���ǁC�^����
�ƕ\����邱�ƂɂȂ�B![]() �́C
�́C![]() ��0����
�n�܂�sine��
��0����
�n�܂�sine��
![]() ��
�����ʑ��̂���ł���B
��
�����ʑ��̂���ł���B
�}-10.3�ɂ��̉^�����������B
�}�Ɏ������悤�ɁC���̈ʒu�ɓ������x�Ŗ߂�܂ł̎���![]() ���ŗL����
�i�P�ʂ�s�j�ƌĂсC�����1�b�Ԃ�
���ŗL����
�i�P�ʂ�s�j�ƌĂсC�����1�b�Ԃ�![]() rad�̑����̉^����
rad�̑����̉^����![]() ���̂�
�K�v�Ȏ��ԂȂ̂�
���̂�
�K�v�Ȏ��ԂȂ̂�
�Ƃ����W�ɂȂ�B���������Ď�(10.8)��
��`�����![]() ���ŗL�U����
10.1�ƌĂԁB
��(10.8)�����i�^���̏ꍇ�̌ŗL�U�����ɂȂ�̂ŁC
��(10.3)�Ǝ�(10.6)�̉^�����������m��
��r����Ζ��炩�Ȃ悤�ɁC�U��q�^���̌ŗL�U������
���ŗL�U����
10.1�ƌĂԁB
��(10.8)�����i�^���̏ꍇ�̌ŗL�U�����ɂȂ�̂ŁC
��(10.3)�Ǝ�(10.6)�̉^�����������m��
��r����Ζ��炩�Ȃ悤�ɁC�U��q�^���̌ŗL�U������
�ƂȂ�B�܂�U��q�̒���![]() ������Ƃ�����蓮���C
�Z������Ƒ����������Ƃ������Ă���B���v���̂��낢���
�U��q���v�i�{���ɐU��q�œ����Ă���̂��˂�?�j��
�������ώ@���Ă݂�Ƃ����B
������Ƃ�����蓮���C
�Z������Ƒ����������Ƃ������Ă���B���v���̂��낢���
�U��q���v�i�{���ɐU��q�œ����Ă���̂��˂�?�j��
�������ώ@���Ă݂�Ƃ����B
���Z�̕����Ŋ��Ɣ����ϕ����g���Ă͂����Ȃ����Ƃ̐���͂Ƃ������C
�L���ȖڂƂ��ďK���Ċo���Ă������̂̍����������Ă������B
��(10.1)�Ńo�l����苎��C����͎��R����
�̉^���������ɂȂ�͂����B
�ȒP�̂��߂ɊO��![]() ���������̂Ƃ���ƁC�����
���������̂Ƃ���ƁC�����
�ł���B�܂�C�����x�����![]() �ł��邱�Ƃ���C�������x�^���ł���B
�������������_�̏����ʒu�Ə����ŗ^���邽�߂ɁC��(10.7)��
�Ȃ����
�ł��邱�Ƃ���C�������x�^���ł���B
�������������_�̏����ʒu�Ə����ŗ^���邽�߂ɁC��(10.7)��
�Ȃ����
�Ƃ��Ă����B��(![]() )��������
)��������
����ʉ��Ȃ̂ŁC��̏��������ɑ�������![]() ,
, ![]() ��
���߂���B���������āC���R�����̎��_�̈ʒu�͉������𐳂Ƃ����
��
���߂���B���������āC���R�����̎��_�̈ʒu�͉������𐳂Ƃ����
�ɂȂ�B���ꂪ�����^���ɂȂ��Ă��邱�Ƃ͂����ɗ����ł���Ǝv���B
�����d�͏�ƒ������鐅���^���̏ꍇ�ɂ́C
���̓��̏d�͉����x![]() �̍�����������̂ŁC����͓����^���ɂȂ�B
�̍�����������̂ŁC����͓����^���ɂȂ�B
�܂���(10.6)�����d�͏�i�����ʓ��j�̉�]�^����
�ꍇ�ɂ́C
![]() �i
�i
![]() �j�̓����x�^���ɂȂ�C������~�^��
�ƌĂԁB
���̂Ƃ����_�̑��x�x�N�g���́C
�j�̓����x�^���ɂȂ�C������~�^��
�ƌĂԁB
���̂Ƃ����_�̑��x�x�N�g���́C![]() ������
������
������
������
![]() �Ƃ����
�Ƃ����
�ł���B������![]() (
(
![]() )��
�e���W�n�̒P�ʊ��x�N�g���ł���B
���ꂩ������x�x�N�g�������߂��
)��
�e���W�n�̒P�ʊ��x�N�g���ł���B
���ꂩ������x�x�N�g�������߂��
�ƂȂ�B�܂�����x��![]() �̕��̕����i��]���S�����j�ɐ����Ă��āC
���̑傫��
�̕��̕����i��]���S�����j�ɐ����Ă��āC
���̑傫��![]() ��
��
�ł���B���̂��Ƃ���C���S��
��
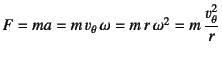 �ƂȂ�̂ł���B
���Z�̋��ȏ��ɍڂ��Ă���U���ߒ��͗����ł��Ȃ����C�������g���ΊȒP���B
�������C��1���҂�50�ɂȂ��ď��߂Ă��ꂪ�킩�����̂����C
�����I�ȈӖ��͖����ɐ����ł��Ȃ��B
�ƂȂ�̂ł���B
���Z�̋��ȏ��ɍڂ��Ă���U���ߒ��͗����ł��Ȃ����C�������g���ΊȒP���B
�������C��1���҂�50�ɂȂ��ď��߂Ă��ꂪ�킩�����̂����C
�����I�ȈӖ��͖����ɐ����ł��Ȃ��B
���āC���R�͂Ƃ肠�����l�����ɁC
��(10.3)��![]() ���悶�Ď��Ԑϕ����Ă݂悤�B
���悶�Ď��Ԑϕ����Ă݂悤�B
�����ŁC��1����
�ƕό`�ł��C��2�������l��
�ƂȂ�̂ŁC�㎮�͌���
����������B������G�l���M�ۑ���
�ł���C![]() ���^���G�l���M
�ł���C
���^���G�l���M
�ł���C![]() ���ʒu�G�l���M
�ł���B�E�ӂ͊O�͂̎��G�l���M�ł���B
�ǂ̏�Ԃ���ɂ���̂����L���Ă��Ȃ��̂ŁC�E�ӂɂ͒萔�̍����c���Ă���B
���R�U���̏ꍇ�̉��̎�(10.11)�ŁC�Ⴆ�Ώ�������̏ꍇ��
������(10.14)�̊e���ɑ�������
���ʒu�G�l���M
�ł���B�E�ӂ͊O�͂̎��G�l���M�ł���B
�ǂ̏�Ԃ���ɂ���̂����L���Ă��Ȃ��̂ŁC�E�ӂɂ͒萔�̍����c���Ă���B
���R�U���̏ꍇ�̉��̎�(10.11)�ŁC�Ⴆ�Ώ�������̏ꍇ��
������(10.14)�̊e���ɑ�������
�ƂȂ�C
![]() �ł��邱�Ƃ��킩��B�܂�
�ł��邱�Ƃ��킩��B�܂�
�ł��邱�Ƃ��킩��B
���̍Ō�̌��_��p����ƁC�������
�ʔ������Ƃ����߂邱�Ƃ��ł���B
�����o�l�ɂ����ʂ�����C�P�ʒ���������̎��ʂ�![]() �ł���
�ꍇ�́C�}-10.4�Ɏ���������
�ł���
�ꍇ�́C�}-10.4�Ɏ���������![]() �̎��_�̐U����
�l���Ă݂悤�B
�L�т̓o�l�̏��������ɔ�ׂď����������ł���Ƃ��āC
�o�l�̒�����
�̎��_�̐U����
�l���Ă݂悤�B
�L�т̓o�l�̏��������ɔ�ׂď����������ł���Ƃ��āC
�o�l�̒�����![]() �Ƃ���B�ȒP�̂��߂ɁC���_�̐U���ɂ��ψʂ�
�Ƃ���B�ȒP�̂��߂ɁC���_�̐U���ɂ��ψʂ�
�Ƃ���ƁC�}���疾�炩�Ȃ悤�ɁC�o�l�̓r���̔C�ӓ_![]() �̕ψ�
�̕ψ�![]() ��
��
�ɂȂ�ƍl���Ă������낤�B�����p���đS�̂̉^���G�l���M�����߂��
�ƂȂ�B����C�ʒu�G�l���M�i�o�l�̑S�ό`���~���Ă���ό`��
�G�l���M�j�̓o�l�̎��ʂƂ͖��W��
�ƂȂ�B���̌��ʂ���(10.15)�ɑ�������
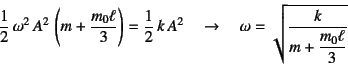
�ƁC�ŗL�U���������߂���B
�Ȃ����C�o�l�̑S����![]() ��
��![]() �����̍v���ɂȂ�B
�����̍v���ɂȂ�B
���āC���ۂɐU�����镨�̂��ώ@����ƁC�Ⴆ��C��R���ɂ���� �U���͂��̂����~�܂��Ă��܂����낤�B���̂悤�� �U���������U���ƌĂԁB���� �̌����́C��C��R�i���x��2��ɔ��j�����ł͂Ȃ��C �ޗ��̒��̉��炩�̔�t�ό`�ŃG�l���M�� �����Ă��܂�����C�\���ƍޗ��̂ǂ����ɖ��C���������Ă�����C ��X�l������B�����ł͂�������f�����������̂̂����C �ł���{�I��2��ށC�܂葬�x�ɔ�Ⴕ���S����R������ꍇ�ƁC ���̗͂ɂ��ő̖��C��R������ꍇ�̐U�����������B
�o�l���ψʂɔ�Ⴕ����R������̂ɑ��āC�S����R�Ƃ����̂͑��x��
��Ⴕ����R�̂��Ƃł���B�T�^�I�ȃ��f����
�悭Kelvin-Voigt���f��
�ƌĂ��n�ŁC�}-10.5�Ɏ������B
�o�l�łȂ����̋L���́C�_�b�V���|�b�g��
�Ă�鑕�u�ŁC���ꂪ�S����R�������Ă���B
�}�̒����ɕ`�����悤�ɁC�����̃I�C�����������ꂽ�V�����_�[�ɁC
���̊J�����s�X�g�������Ă�����̂��v���`���ė~�����B
�s�X�g����������蓮�����ƃI�C���͌����X���[�Y��
�ʂ蔲���C�قƂ�ǒ�R���������Ȃ��B�����������s�X�g����
���������Ƃ����ꍇ�ɂ́C�I�C���͂���قǑ����͌���ʂ蔲����ꂸ�C
���ꂪ��R�͂ɂȂ�B���̂悤�ɁC���x�ɔ�Ⴕ����R��
�������Ă���̂��_�b�V���|�b�g�ł���C���̔��W����![]() �Ƃ���B
�}�̉E�[�̗͂̃_�C�A�O�����̂悤�ɁC���_�ɂ̓_�b�V���|�b�g����
�������
�Ƃ���B
�}�̉E�[�̗͂̃_�C�A�O�����̂悤�ɁC���_�ɂ̓_�b�V���|�b�g����
�������![]() �̒�R����̂ŁC�^����������
�̒�R����̂ŁC�^����������
�ƂȂ�B������
(10.17)
�ƒ�`����ƁC�O��![]() ����p���Ă��Ȃ����R�U���̏ꍇ�ɂ́C
��̉^��������(10.16)��
����p���Ă��Ȃ����R�U���̏ꍇ�ɂ́C
��̉^��������(10.16)��
�Ə������Ƃ��ł���B������![]() ���S�������W��
�ƌĂ�C
���S�������W��
�ƌĂ�C![]() �́i�S���j�����萔10.2
�ƌĂ��B
�́i�S���j�����萔10.2
�ƌĂ��B
��(10.18)�̉���
![]() �ƒu��
�������ƁC
�ƒu��
�������ƁC![]() �ɂ��Ă̓����������Ƃ��̍���
�ɂ��Ă̓����������Ƃ��̍���
�Ƌ��߂���B
����ɑΉ��������![]() �̑傫���ɂ���ĈقȂ鋓����
�\�����邱�ƂɂȂ�B
�̑傫���ɂ���ĈقȂ鋓����
�\�����邱�ƂɂȂ�B
�ƒu�����Ƃ��ł���B���̏ꍇ�ɂ́C����
�ƂȂ�B�܂�C�U��![]() ���w�����I�ɏ������Ȃ�Ȃ���i�㎮��
�b���ʕ����j�U�����邱�Ƃ�
�Ȃ�B�}-10.7�̍��}�ɂ��̗���������B
�U���̃s�[�N������_�������w�����I�ɏ������Ȃ�l�q��
�����Ă���C�U���͂��̔䗦�ŏ������Ȃ��Ă������C
�����͈��̂܂܂̐U���ł���B
���w�����I�ɏ������Ȃ�Ȃ���i�㎮��
�b���ʕ����j�U�����邱�Ƃ�
�Ȃ�B�}-10.7�̍��}�ɂ��̗���������B
�U���̃s�[�N������_�������w�����I�ɏ������Ȃ�l�q��
�����Ă���C�U���͂��̔䗦�ŏ������Ȃ��Ă������C
�����͈��̂܂܂̐U���ł���B
���āC���̍Ō��![]() �̏ꍇ�Ɍ��肵�āC�ȉ��̐�����
�����邱�Ƃɂ��悤�B���̂悤��
�����U���̏ꍇ�̐U�����͎�(10.19)��
�̏ꍇ�Ɍ��肵�āC�ȉ��̐�����
�����邱�Ƃɂ��悤�B���̂悤��
�����U���̏ꍇ�̐U�����͎�(10.19)��![]() �ł��邩��C
����
�ł��邩��C
����![]() ��
��
�ɂȂ�B
��ʂɑO�q�̂悤�ɁC�Љ��Ս\���̏ꍇ�͌����萔![]() �͔��ɏ������C
�Ⴆ�|�\���ł�0.02�`0.03�C�R���N���[�g�\���ł�0.03�`0.05��
�l���Ă������߁C
�͔��ɏ������C
�Ⴆ�|�\���ł�0.02�`0.03�C�R���N���[�g�\���ł�0.03�`0.05��
�l���Ă������߁C![]() ��
��![]() �̍��͖����ł��邭�炢������
�̍��͖����ł��邭�炢������
�Ƌߎ����Ă������̂����ʂł���B
���ۂ̎Љ��Ս\���̌������S�������ł���Ƃ͌���Ȃ����C
����łقڋߎ��ł��C�܂��ߎ��ł���ƕ֗��Ȃ̂ŁC
�S���������f����p���Ă���̂��낤��
�v����B�ł́C����������������S�������萔�����߂邱�Ƃ�
�l���Ă݂悤�B�����f�[�^���}-10.7�̉E�}�̂悤
�������Ƃ��悤�B![]() �Ԗڂ̐U����
�Ԗڂ̐U����![]() �Ԗڂ̐U���i�}�ł�
�Ԗڂ̐U���i�}�ł�![]() �j��
���ꂼ��
�j��
���ꂼ��![]() ,
, ![]() �Ƃ���ƁC
���̐U����i�ʏ��
�Ƃ���ƁC
���̐U����i�ʏ��![]() �j��������
10.3�ƌĂсC����͗��_�I�ɂ�
�j��������
10.3�ƌĂсC����͗��_�I�ɂ�
�ƂȂ�̂ŁC�萔�ɂȂ�B���������āC���̊W����p���č\�����̐U��������
�����l������C��������̌����萔![]() ���t�Z���邱�Ƃ��ł���B
�܂��C���̌�����̑ΐ����ΐ�������
�ƌĂԁi
���t�Z���邱�Ƃ��ł���B
�܂��C���̌�����̑ΐ����ΐ�������
�ƌĂԁi![]() �̏ꍇ�Œ�`����Ă���̂����ʁj���C�����
�̏ꍇ�Œ�`����Ă���̂����ʁj���C�����
�ƂȂ�C������萔�Ȃ̂ŁC���̊W������
�ƁC�����萔�����߂邱�Ƃ��ł���B���邢�́C![]() ��
��������Ȃ�C���̊W�͂����Ƌߎ��ł���
��
��������Ȃ�C���̊W�͂����Ƌߎ��ł���
�Ƃ��Ă��������ƂɂȂ�B
�}-10.8�ɂ́C
�w�������œ���1���R�x�n�̉����x�L�^���~�_�Ŏ������B
�����ł́C�|�̔��Ŕo�l�����C���̐�[�ɏd������t���C
�o�l�������Ȃ�����ԂŎ�𗣂��C���̂��Ƃ̎��R�U����
�d��̉����x���L�^�����B�������Ƃ��̗��ꂪ�m�C�Y�Ƃ���
�^���ɉe�����y�ڂ��̂ŁC������Ԃ��琔�����o�����Ƃ̋L�^���C
���R�U�����Ă���Ɣ��f���Đ}�������B![]() �͏\����������
���肵����ŁC���̋L�^�̉������܂���15�������̎��Ԃ���
������
�͏\����������
���肵����ŁC���̋L�^�̉������܂���15�������̎��Ԃ���
������![]() s�Ɠǂݎ��C
�ߎ���(10.23)����ŗL�U������
s�Ɠǂݎ��C
�ߎ���(10.23)����ŗL�U������![]()
![]() �Ɠ��肵���B
����ɁC���̐}�͈̔͂̐������̐U���f�[�^��p���āC
���낢���
�Ɠ��肵���B
����ɁC���̐}�͈̔͂̐������̐U���f�[�^��p���āC
���낢���![]() ��
��![]() �Ŏ�(10.25)��
�ߎ���(10.27)��p���ĎZ�肵�����̂�
���ς��āC
�Ŏ�(10.25)��
�ߎ���(10.27)��p���ĎZ�肵�����̂�
���ς��āC![]() �Ɠ���ł����B
���肵���p�����[�^��p���ċ��߂������������ŁC
�قƂ�Ǐd�Ȃ��Ă��邱�Ƃ��킩��B
���ۂ̎������u�ł́C���ɔS������������L�������u��t�����킯�ł��Ȃ��C
�������闝�R�͋�C��R��o�l�̎��t�����ɂ����鉽�炩��
�G�l���M���������낤�Ɨ\�z����邪�C�����I�ȋ����𑨂������́C
���̒��x�̃V�~�����[�V�������\�ɂȂ��Ă��邱�Ƃ���C�Љ��Ս\����
�U�����f���ɂ����Ă��C�S���������f�����p�����Ă���̂ł��낤�B
�Ɠ���ł����B
���肵���p�����[�^��p���ċ��߂������������ŁC
�قƂ�Ǐd�Ȃ��Ă��邱�Ƃ��킩��B
���ۂ̎������u�ł́C���ɔS������������L�������u��t�����킯�ł��Ȃ��C
�������闝�R�͋�C��R��o�l�̎��t�����ɂ����鉽�炩��
�G�l���M���������낤�Ɨ\�z����邪�C�����I�ȋ����𑨂������́C
���̒��x�̃V�~�����[�V�������\�ɂȂ��Ă��邱�Ƃ���C�Љ��Ս\����
�U�����f���ɂ����Ă��C�S���������f�����p�����Ă���̂ł��낤�B
�ő̖��C�̃��f�����l����O�ɁC
��(10.9)�̉^����������ψʂƑ��x�̕��ʏ��
�\�����Ƃ��l���悤�B���̂悤�ȕ��ʂ��ʑ�����
�ƌĂсC�����蓙�ł��p�����邱�Ƃ�����B
�܂��^���������̉����x����
�Ə��������Ă���������C�^����������
�ƂȂ�̂ŁC��������ʂɐϕ������
�ƕ\�����Ƃ��ł���B�E�ӂ̒萔�͏��������Ō��܂�l�ł���B
�U���ߒ�����������ł���悤�ɁC����̓G�l���M�ۑ������̂��̂ł�����B
���̎���![]() ��
��![]() ��2���Ƃ���ʑ����ʏ�őȉ~����O��
��`�����Ƃ��Ӗ����Ă���B
���邢�́C���ɂ��̏ꍇ�ɂ�
��2���Ƃ���ʑ����ʏ�őȉ~����O��
��`�����Ƃ��Ӗ����Ă���B
���邢�́C���ɂ��̏ꍇ�ɂ�![]() ��
��
![]() ��2���ɂ���
�~�O���ɂȂ�B
��2���ɂ���
�~�O���ɂȂ�B
���āC�}-10.9�Ɏ������悤�ɁC���_�Ƃ�
�ԂɈ��̓����C��![]() �i
�i![]() �͓����C�W��
�j���������鏰�̏�̐U��10.4���l���Ă݂悤�B
���x�Ƌt�̌����ɖ��C����������̂ŁC
�͓����C�W��
�j���������鏰�̏�̐U��10.4���l���Ă݂悤�B
���x�Ƌt�̌����ɖ��C����������̂ŁC![]() �̂Ƃ��̉^����������
�̂Ƃ��̉^����������
�ƂȂ�̂ɑ��C![]() �̏ꍇ�ɂ�
�̏ꍇ�ɂ�
�ƂȂ�B���������āC������܂Ƃ߂��
�Ə���10.5���Ƃ��ł���B
������Sgn�͈����̕�����\���L����
�ƒ�`�����B���������͎�(10.7)�ŗ^������B ���̔����������x�̕����ŏꍇ���������Ď��X���X�����Ă����� �������߂邱�Ƃ��ł��邪�C�����ł͏�q�̈ʑ����ʂ��g���Ă݂悤�B
���̉^��������(10.29)�ɑ�������ʑ����ʏ�̋O�������߂悤�Ƃ���ƁC
�܂�
�Ƃ��Ă���������C�ʑ����ʂ�
�ƕ\�����Ƃ��ł���B
�܂�}-10.10�Ɏ������悤�ɁC
���x�̌������ς��x�ɉ~�̒��S�ʒu
![]() ���ˑR�ړ�����B
�ʑ����ʂ́C���x����������ɕψʎ����E�����ɕ`���̂����ʂ����C
������������`���Ղ��悤�ɁC�����v����90�x��]���ĕ`�����B
���������̏�Ԃ��玞�v���ɉ�]���Ȃ���C�ψʎ����܂�������������
�O���̒��S���ˑR�ړ����C����ɔ����U�����������Ȃ��Ă����C
�Ō��
���ˑR�ړ�����B
�ʑ����ʂ́C���x����������ɕψʎ����E�����ɕ`���̂����ʂ����C
������������`���Ղ��悤�ɁC�����v����90�x��]���ĕ`�����B
���������̏�Ԃ��玞�v���ɉ�]���Ȃ���C�ψʎ����܂�������������
�O���̒��S���ˑR�ړ����C����ɔ����U�����������Ȃ��Ă����C
�Ō��
![]() �̏��10.6�ő��x����ɂȂ�
���_�i���̈ʑ����ʂ̐}�̏c����j�Ŏ~�܂邱�ƂɂȂ�B
�̏��10.6�ő��x����ɂȂ�
���_�i���̈ʑ����ʂ̐}�̏c����j�Ŏ~�܂邱�ƂɂȂ�B
���Ȃ݂ɁC��(10.14)�̗U���Ɠ����A�v���[�`�ŁC
�ő̖��C������ꍇ�̃G�l���M�ۑ�����U�����Ă������B
��(10.29)�̉^����������![]() ���悶�Đϕ�����ƁC
�ŏ���2���͎�(10.14)�Ɠ������_�ɂȂ�B��3����
���悶�Đϕ�����ƁC
�ŏ���2���͎�(10.14)�Ɠ������_�ɂȂ�B��3����
�ɂȂ�B��������Z�ŏK���Ċo���������ł��낤�B���������āC
�G�l���M�ۑ����́C�O�͍����܂߂��
�ƂȂ�B
�����܂ł͊O��![]() ����p���Ă��Ȃ����̂Ƃ��āC
�U���̍ł���{�I�ȃp�����[�^�ł���ŗL�U������
�����萔�̈Ӗ��ɂ��Đ������Ă����B
���ۂɂ́C�n�k�╗�⊈�d�Ƃ������O�͂���p�����ł̐U����
���ɂȂ�C���̂悤�ȊO�͂ɑ��Ĉ��S�ȎЉ��Ս\����
�Ȃ�悤�ɁC�ŗL�U�����i�⌸���萔�j��v����K�v������B
�����ł́C��������\�I�ȊO�͂����݂���ꍇ�̐U����ΏۂƂ��āC
���̊�{�I�ȓ�̃p�����[�^�ƊO�͓����̊W�ɂ��Č������悤�B
�O��
����p���Ă��Ȃ����̂Ƃ��āC
�U���̍ł���{�I�ȃp�����[�^�ł���ŗL�U������
�����萔�̈Ӗ��ɂ��Đ������Ă����B
���ۂɂ́C�n�k�╗�⊈�d�Ƃ������O�͂���p�����ł̐U����
���ɂȂ�C���̂悤�ȊO�͂ɑ��Ĉ��S�ȎЉ��Ս\����
�Ȃ�悤�ɁC�ŗL�U�����i�⌸���萔�j��v����K�v������B
�����ł́C��������\�I�ȊO�͂����݂���ꍇ�̐U����ΏۂƂ��āC
���̊�{�I�ȓ�̃p�����[�^�ƊO�͓����̊W�ɂ��Č������悤�B
�O��![]() ����p�����U���������U���ƌĂԁB
��ʓI�Ȗ��Ƃ��āC��(10.16)��
�������B���邢��
����p�����U���������U���ƌĂԁB
��ʓI�Ȗ��Ƃ��āC��(10.16)��
�������B���邢��![]() �ŏ����C��(10.18)�̌`�ɂ����
�ŏ����C��(10.18)�̌`�ɂ����
�ƂȂ�B
�܂���{�I�ȊO�͂Ƃ��Đ����g��̊O�͂������B�Ƃ����̂��CFourier������
�v���o���C�C�ӂ̂ق��ǂ̊��͎O�p���ŕ\���ł���ƍl����
�������낤����C
���̊�{�I�ȊO�͂Ƃ���
![]() �ɂ��čl���Ă����C
�قƂ�ǂ��ׂĂ̊O�͂ɑ��鉞�������߂��b�ɂȂ�ƍl�����邩�炾�B
�܂�C��(10.32)��
�ɂ��čl���Ă����C
�قƂ�ǂ��ׂĂ̊O�͂ɑ��鉞�������߂��b�ɂȂ�ƍl�����邩�炾�B
�܂�C��(10.32)��
�ƂȂ�B
��ʉ��́C���R�U���ŋ��߂��Ď����ƊO�͂ɒ��ڊW��������Ƃ̘a�ɂȂ邩��
�ƕ\�����B���������݂���ꍇ�ɂ́C���R�U�����͌������ł���C
���ԂƂƂ��Ɍ������Ă����悤���ߓn����
�ł��邩��C�H�w�I�Ɉ�ԋ���������͓̂����̕�10.7�ɂȂ�B
�����ł����ł͓���![]() ���������߂Ă݂悤�B
���������߂Ă݂悤�B
���w�ŏK���������̋��ߕ���p����̂��]�܂������C����![]() ,
, ![]() ��
���̌��ɂȂ�Ɨ\�z�����̂�
��
���̌��ɂȂ�Ɨ\�z�����̂�
�ƒu���āC��(10.33)������悤��![]() ,
, ![]() �����߂悤�B
�������sine, cosine���ɐ��������
�����߂悤�B
�������sine, cosine���ɐ��������
�ƂȂ�̂�
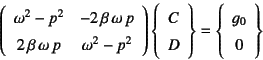
�����������B![]() �̍s��Ȃ̂ŁC�ȒP�ɋt�s���߂��
�̍s��Ȃ̂ŁC�ȒP�ɋt�s���߂��
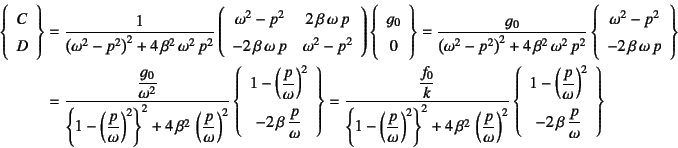
�ƂȂ�B���������ē�����
�Ƌ��߂���B���邢��
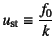 �ƒ�`�����
�ƒ�`�����
(10.35)
�Ə������Ƃ��ł���B![]() �͊O�͂̍ő�l
�͊O�͂̍ő�l![]() ���ÓI�ɍ�p������
�z�肵���Ƃ��̐ÓI�ȕψʂł���B
����������
���ÓI�ɍ�p������
�z�肵���Ƃ��̐ÓI�ȕψʂł���B
����������![]() �́C���̐ÓI�ȕψʂɑ��铮�I�ȕψʂ̊�����
�\���Ă���̂ŁC���I������
�ƌĂ��B
�́C���̐ÓI�ȕψʂɑ��铮�I�ȕψʂ̊�����
�\���Ă���̂ŁC���I������
�ƌĂ��B![]() �́C�����ɂ��ʑ��̒x���
�\������B�}-10.12��
�́C�����ɂ��ʑ��̒x���
�\���Ă���B�}-10.12��![]() �t�߂��g�傷��C
���̈ʑ��̒x��������ł���B
�t�߂��g�傷��C
���̈ʑ��̒x��������ł���B
![]() ��
��![]() ��}-10.11�Ɏ������B
����
��}-10.11�Ɏ������B
����![]() �̏ꍇ�ɂ́C
�̏ꍇ�ɂ́C![]() ��
��
![]() �ƂȂ�C
�܂蔭�U���Ă��܂��B���̌��ۂ����U
�ƌĂсC
�ƂȂ�C
�܂蔭�U���Ă��܂��B���̌��ۂ����U
�ƌĂсC![]() �̂��̐}�̋Ȑ������U�Ȑ��ƌĂԂ��Ƃ�����B
�O�q�̂悤�ɁC�Љ��Ս\����
�̂��̐}�̋Ȑ������U�Ȑ��ƌĂԂ��Ƃ�����B
�O�q�̂悤�ɁC�Љ��Ս\����![]() �͔��ɏ��������߁C
���̂悤�ȋ��U�ɋ߂����ۂ�������\��������B
�͔��ɏ��������߁C
���̂悤�ȋ��U�ɋ߂����ۂ�������\��������B![]() �����ɏ������ꍇ
�����ɏ������ꍇ
�ƂȂ�B
���āC�Љ��Ս\����v�����Ƃ��悤�B
����͍\���̎���![]() �ƍ���
�ƍ���![]() ��
�v�������Ƃɑ������邩��C���I�ɏd�v�ȃp�����[�^�̈��
�ŗL�U����
��
�v�������Ƃɑ������邩��C���I�ɏd�v�ȃp�����[�^�̈��
�ŗL�U����![]() ��v�������ƂɂȂ�B
�����C���̍\���ɍ�p����O�͂̎��g��
��v�������ƂɂȂ�B
�����C���̍\���ɍ�p����O�͂̎��g��![]() �����̌ŗL�U�����ɋ߂��ꍇ�ɂ́C
���U���ĉ����̐U���͔��ɑ傫���Ȃ�C�\���͔j�邩������Ȃ��B
���I�Ȑv�Ƃ����̂́C�ȒP�Ɍ����ƁC���������m�F�����邱�Ƃł���B
�����̌ŗL�U�����ɋ߂��ꍇ�ɂ́C
���U���ĉ����̐U���͔��ɑ傫���Ȃ�C�\���͔j�邩������Ȃ��B
���I�Ȑv�Ƃ����̂́C�ȒP�Ɍ����ƁC���������m�F�����邱�Ƃł���B
�ł͈��Ƃ��āC�ߓn�������܂߂āC�돉�������܂�![]() ,
, ![]() �̏ꍇ��
�����U�����������߂Ă������B
��(
�̏ꍇ��
�����U�����������߂Ă������B
��(![]() )�Ɏ�(10.34)�������C�����돉�������ɑ������ƁC
��̐ϕ��萔��
)�Ɏ�(10.34)�������C�����돉�������ɑ������ƁC
��̐ϕ��萔��
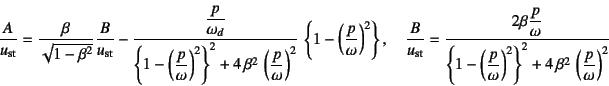
�Ƌ��߂邱�Ƃ��ł���B�㎮��![]() �̉E�ӂɁC
�̉E�ӂɁC![]() �̌��ʂ�
�������Ή������߂���B��Ƃ���
�̌��ʂ�
�������Ή������߂���B��Ƃ���
![]() ��
��![]() ��
�Ƃ��̉���`�����̂��}-10.12�ł���B
���������̉����ŁC�돉�������Ŏn�܂��Ă��邱�Ƃ��킩��B
�j���́C���̉����̒���
��
�Ƃ��̉���`�����̂��}-10.12�ł���B
���������̉����ŁC�돉�������Ŏn�܂��Ă��邱�Ƃ��킩��B
�j���́C���̉����̒���![]() �ŐU�����鐬���C
�܂�ߓn�����̐����ł���B�����萔���傫�߂Ȃ̂ʼnߓn������
�U���͑����������Ȃ��Ă����B���̐����������Ȃ��Ă��܂��C
�����̐U���́C��(10.35b)��
�ŐU�����鐬���C
�܂�ߓn�����̐����ł���B�����萔���傫�߂Ȃ̂ʼnߓn������
�U���͑����������Ȃ��Ă����B���̐����������Ȃ��Ă��܂��C
�����̐U���́C��(10.35b)��![]() �ɂȂ�C
���g����
�ɂȂ�C
���g����![]() �̐U���݂̂��c�邱�ƂɂȂ�B
�}���̐�����2�{�̔j�����C����
�̐U���݂̂��c�邱�ƂɂȂ�B
�}���̐�����2�{�̔j�����C����![]() �̒l�ł���B
���U�_��90%���x�̊O�͎��g���ł��C
�ÓI�ψʂ�5�{���̑傫�ȓ��I�ȕψʂ������Ă��邱�Ƃ��C
���̉����}������킩��B
�܂��C�ߓn�������܂߂��S�U�������I���������傫���Ȃ邱�Ƃ��m�F�ł���B
�̒l�ł���B
���U�_��90%���x�̊O�͎��g���ł��C
�ÓI�ψʂ�5�{���̑傫�ȓ��I�ȕψʂ������Ă��邱�Ƃ��C
���̉����}������킩��B
�܂��C�ߓn�������܂߂��S�U�������I���������傫���Ȃ邱�Ƃ��m�F�ł���B
���āC�n�k�ɑ��鉞���̂��Ƃ��v���`���ƁC
�\�������̂ɊO�͂���p���Ă���O�߂̂悤�ȏł͂Ȃ��C
�o�l�̎x�_�������I�ɕψʂ�����ꂽ�ł̐U���̂悤�Ɍ�����B
�����ł́C���̂悤�ȏ̃��f�����l���Ă݂悤�B�}-10.13��
�������悤�ɁC�x�_�����������ɋ����I��![]() �����ψʂ�����ꂽ
�ꍇ�̎��_�̐����^��
�����ψʂ�����ꂽ
�ꍇ�̎��_�̐����^��![]() ���l���悤�B
�o�l�ƃ_�b�V���|�b�g�́C�x�_�̉^���Ƃ̑��ΕψʂƑ��Α��x��
��Ⴕ����R�͂������܂Ȃ�����C�^����������
���l���悤�B
�o�l�ƃ_�b�V���|�b�g�́C�x�_�̉^���Ƃ̑��ΕψʂƑ��Α��x��
��Ⴕ����R�͂������܂Ȃ�����C�^����������
�ƂȂ�BNewton�̖@���̊������͐�Ή����x![]() �ŕ\����Ă���̂ŁC
��1���͂���܂łƓ����ł���B���Ă����ŁC�x�_�̕ψʂɑ���
���ΓI�Ȏ��_�̕ψ�
�ŕ\����Ă���̂ŁC
��1���͂���܂łƓ����ł���B���Ă����ŁC�x�_�̕ψʂɑ���
���ΓI�Ȏ��_�̕ψ�
��p���āC��̉^��������(10.36)������������
�Ə������Ƃ��ł���B���̎��Ǝ�(10.16)���r�����
���炩�Ȃ悤�ɁC�x�_�̋����ψʂɑ��鑊�ΓI�ȉ���![]() �́C
��������
�́C
��������
�̊O�͂����ڎ��_�ɍ�p�����Ƃ��̋����O�͉����Ɠ����ł��邱�Ƃ��킩��B ���̎�(10.39)�͔��ɏd�v�ȊT�O�ł���C �ϐk�v�ɂ����ėp�����Ă����k�x�@ �̍����ɂȂ��Ă���B�܂�C�ߋ��Ɋϑ����ꂽ��n�k�� �̒n�k�����x���Q�l�ɂ��Đݒ肳�ꂽ�v���͒n�k�����x�ɁC �v����悤�Ƃ��Ă���Љ��Ս\���̎��ʂ��悶�邱�Ƃɂ���āC ���̍\���ɍ�p������ׂ��n�k�O�͂��Z�肵�C�������p�������Ƃ��� �\���̒�R���ƍ����邱�Ƃɂ���āC�ϐk�v���ł��邱�Ƃ������Ă���B
��{�I�ȗ�Ƃ��āC�x�_�ψʂ������g���
�ƂȂ�ꍇ���㎮(10.38)�ɑ������ƁC�^����������
�ƂȂ�B���������āC�O�߂̊O�͂̐U����
![]() �ƒu��������C
���̂܂ܑO�߂̉��𗬗p�ł���̂ŁC
�����͎�(10.35)�Ƃقړ��l�ɂȂ�
�ƒu��������C
���̂܂ܑO�߂̉��𗬗p�ł���̂ŁC
�����͎�(10.35)�Ƃقړ��l�ɂȂ�
�ƂȂ�B�ʑ��̒x��![]() �͎�(10.35c)�Ɠ����ɂȂ�B
��(10.41)�̓��I������
�͎�(10.35c)�Ɠ����ɂȂ�B
��(10.41)�̓��I������![]() ��}-10.14��
�������B�܂�
��}-10.14��
�������B�܂�
�Ƃ������Ƃ��킩��B
�Ƃ���ŁC�n�k�v
�Ƃ����͈̂�̂ǂ��Ȃ��Ă���낤�B
�n�ʂƈꏏ�ɓ����Ă���n�k�v���C�������g�̉^�����L�^�ł���̂�
��ɂ͊����Ȃ����낤���B
���̋^��ɓ����Ă����̂��C�����ŋ��߂�ꂽ���ł���B
�܂�C�n�k�v�͂����Œ�`�������Εψ�![]() ���L�^���ɏ�������ł���
�̂�����C
���Εψ�
���L�^���ɏ�������ł���
�̂�����C
���Εψ�![]() �̋������l����C�n�k�v�̌����������ł���͂����B
�Ⴆ�C�n�k�v��
�̋������l����C�n�k�v�̌����������ł���͂����B
�Ⴆ�C�n�k�v��![]() ��
��![]() ��K�ɐv���āC�ϑ��������n�k����
�U����
��K�ɐv���āC�ϑ��������n�k����
�U����![]() �ɑ���
�ɑ���
![]() �ɂȂ�悤�ɐ��삵���Ƃ��悤�B
����ƁC��ŋ��߂�ꂽ������
�ɂȂ�悤�ɐ��삵���Ƃ��悤�B
����ƁC��ŋ��߂�ꂽ������
�ɂȂ�B�܂�C�n�ʂ̕ψʉ������L�^���邱�Ƃ��ł���B
����ƑΏƓI�ɒn�k�v��![]() ��
��![]() ������
������
![]() ��
�Ȃ�悤�ɐ��삵���Ƃ��悤�B���̏ꍇ�ɂ�
��
�Ȃ�悤�ɐ��삵���Ƃ��悤�B���̏ꍇ�ɂ�
![]() �ł��邱�Ƃ���C
��(10.41)����
�ł��邱�Ƃ���C
��(10.41)����
�ƂȂ��Ă��邱�Ƃ��킩��B�܂莮(10.40)�̔��W���Ɣ�r����
�ƍl���Ă������ƂɂȂ�B ���������āC�n�ʂ̉����x�������L�^�ł���̂ł���B������ƕs�v�c�B
���ɁC�����O�͂Ƃ͐����̓����������낤�ƍl������Ռ��O�͂�
��p�����Ƃ��̐U���ɂ��čl���Ă݂悤�B
�܂��C�Ռ����̂��̂��ǂ̂悤�Ƀ��f�������邩�����ɂȂ邾�낤�B
�����_![]() �ɁC����
�ɁC����![]() �ɁC�P�ʗʂ̏Ռ��O��
�ɁC�P�ʗʂ̏Ռ��O��![]() ����p�������Ƃ���B
�Ռ��Ȃ̂ŁC���ɒZ������
����p�������Ƃ���B
�Ռ��Ȃ̂ŁC���ɒZ������![]() ������p���Ă���Ƃ��悤�B
���̂Ƃ��̎��_��
�^����������
������p���Ă���Ƃ��悤�B
���̂Ƃ��̎��_��
�^����������
![]() ����
����
![]() �܂�
�ϕ�����ƁC�܂���������
�܂�
�ϕ�����ƁC�܂���������
�ƂȂ�B����C�o�l�̒�R�̍��͈ʒu�G�l���M�̒Z���Ԃ̕ω����ł���C
�S����R���Z���Ԃ̑��x�ω��ɂȂ�̂ŁC
���̎��̂悤��![]() �̋Ɍ��ł͗�C�܂�
�̋Ɍ��ł͗�C�܂�
�ł���B���������āC�^����������ϕ��������̂͌���
�ƂȂ�B���̎��́C�����^���ʕۑ���
�ł���C�E�ӂ͏Ռ��O��![]() �ɂ��͐ςł���B
�ɂ��͐ςł���B
���̗͐ς��P�ʗʁC�܂�1�̂Ƃ��̊O��![]() ���P�ʏՌ��O��
�ƌĂԂ��Ƃɂ��悤�B��Ƃ��ċ������̂��}-10.15�ł���B
���̂悤�Ȋ�
���P�ʏՌ��O��
�ƌĂԂ��Ƃɂ��悤�B��Ƃ��ċ������̂��}-10.15�ł���B
���̂悤�Ȋ�![]() �́C�W������f�O�͂����f���������Ƃ���
��(4.55)��Dirac�̃f���^��
�́C�W������f�O�͂����f���������Ƃ���
��(4.55)��Dirac�̃f���^�� ![]() �Ɠ����ł���C
�����
�Ɠ����ł���C
�����
�ƂȂ�B���̎��_������![]() �܂ŐÎ~���Ă����Ƃ���ƁC
�܂ŐÎ~���Ă����Ƃ���ƁC![]() ��
�Ɍ��ɂ����Ď�(10.42)�̍��ӑ�2���͗�ɂȂ�̂�
��
�Ɍ��ɂ����Ď�(10.42)�̍��ӑ�2���͗�ɂȂ�̂�
�ƂȂ�B���������āC1���_�n�Ɏ���![]() �ɒP�ʏՌ��O�͂���p������
�Ƃ��̏����l����
�ɒP�ʏՌ��O�͂���p������
�Ƃ��̏����l����![]() �ɂ�����
�ɂ�����
�ŗ^�����邱�ƂɂȂ�B�������![]() �ɂ������Ԃ�
�ɂ������Ԃ�![]() �ł���B
�ł���B
��(10.44)�̈�ʉ���
�Ȃ̂ŁC��������������ɑ�������
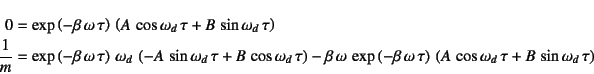
�����Ȃ���Ȃ�Ȃ��B����������
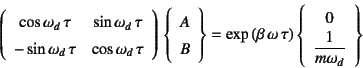
�ƂȂ�̂ŁC�����������
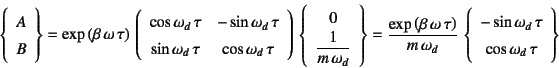
�̂悤�ɐϕ��萔�����߂���B���������ĉ���
�Ƌ��߂���B������P�ʏՌ�����
�ƌĂ�ł���B�Ռ����^����ꂽ����![]() �����̈�����
��������̂����ʂł���C�܂����̌`���疾�炩�Ȃ悤�ɁC
�����
�����̈�����
��������̂����ʂł���C�܂����̌`���疾�炩�Ȃ悤�ɁC
�����![]() �݂̂̊��ł��邱�Ƃ���C
������O�ڂ̕\�����悭�p������B
�݂̂̊��ł��邱�Ƃ���C
������O�ڂ̕\�����悭�p������B
���āC��(10.45)�Ɏ������悤�ɁC
����![]() ��
��![]() �̑O��ɏꍇ�������ē�̒�`������̂͂ƂĂ��ʓ|�����C
�g����̂ŁC�������̎��ɂ܂Ƃ߂Ă݂����B���̂��߂�
�̑O��ɏꍇ�������ē�̒�`������̂͂ƂĂ��ʓ|�����C
�g����̂ŁC�������̎��ɂ܂Ƃ߂Ă݂����B���̂��߂�
�ƒ�`�����Heaviside���i�K�i���j
�����Ă݂悤�B
�Ȃ��㎮��
![]() �͎�(10.43)�Œ�`����Dirac��
�f���^���ŁC��������������͊��ł͂Ȃ������ł��邩��C
�Ō�̎��̓���
�͎�(10.43)�Œ�`����Dirac��
�f���^���ŁC��������������͊��ł͂Ȃ������ł��邩��C
�Ō�̎��̓���
![]() ��
�����̂��߂̓���ȓ����ł���B
���āC����Heaviside���̐����𗘗p����C�C�ӎ���
��
�����̂��߂̓���ȓ����ł���B
���āC����Heaviside���̐����𗘗p����C�C�ӎ���![]() ��
�P�ʏՌ�������
��
�P�ʏՌ�������
�Ə������Ƃ��ł���B���̏ꍇ��![]() �Ȃ̂�
�Ȃ̂�
�ƂȂ�B���̐߈ȍ~�ŁC���̕\���͂ƂĂ��֗����Ƃ������Ƃ��킩��B
�Ȃ��C�����l���̏���������(10.44)����
���炩�Ȃ悤�ɁC�P�ʏՌ������͎���![]() �ɂ�����돉��������
���ł͂Ȃ����Ƃɂ͏\�����ӂ���K�v������B
�ɂ�����돉��������
���ł͂Ȃ����Ƃɂ͏\�����ӂ���K�v������B
�ł́C�傫�����P�ʗʂł͂Ȃ��C�}-10.17��
����̐}�̂悤�ɁC�ʐς�![]() �̏Ռ��O�͂ɑ��鉞����
�̏Ռ��O�͂ɑ��鉞����
�ƂȂ邱�Ƃ́C�N���^��ɂ͎v��Ȃ����낤�B
����Ȃ�C���̉E�̐}�̂悤�ɁC�O�̈قȂ�傫����
�Ռ��O�͂ɑ��鉞����
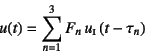
�ɂȂ�̂��[�����Ă��炦��Ǝv���B����C�C�ӎ���![]() ��
�����͏ꍇ���������Ȃ��Ƃ����Ȃ�����C�O�������Ă��܂��Ă�
�����Ȃ��̂ł͂Ȃ����Ǝv���l��
���邩������Ȃ����C�Ⴆ�Ώ㎮�̑��a�̑�2����
��
�����͏ꍇ���������Ȃ��Ƃ����Ȃ�����C�O�������Ă��܂��Ă�
�����Ȃ��̂ł͂Ȃ����Ǝv���l��
���邩������Ȃ����C�Ⴆ�Ώ㎮�̑��a�̑�2����
�ł���CHeaviside�����܂܂�Ă��邩��![]() �̊Ԃ͖����̂Ɠ����ł���B
���������āC�C�ӂ̎���
�̊Ԃ͖����̂Ɠ����ł���B
���������āC�C�ӂ̎���![]() �ɑ����̉��̕\���ɂ͎O��
�����Ă����Ă����̂ł���BHeaviside���͕֗��ł���B
�ɑ����̉��̕\���ɂ͎O��
�����Ă����Ă����̂ł���BHeaviside���͕֗��ł���B
����ł͐}-10.17�̉��̐}�̂悤��
�C�ӂ̊�![]() �ŕ\���ꂽ�O�͂ɑ��鉞�����C���l�ɁC�P�ʏՌ�������
�p���ĕ\���ł��Ȃ��ł��낤���B
�l���Ղ����邽�߂ɁC�}�̂悤�ɁC
�ŕ\���ꂽ�O�͂ɑ��鉞�����C���l�ɁC�P�ʏՌ�������
�p���ĕ\���ł��Ȃ��ł��낤���B
�l���Ղ����邽�߂ɁC�}�̂悤�ɁC![]() ���̒Z����
���čl����ƁC�Ⴆ�ΖԊ|�����������́C�ʐ�
���̒Z����
���čl����ƁC�Ⴆ�ΖԊ|�����������́C�ʐ�
![]() ��
�Ռ��Ƃ��Ď�舵���������Ƃ��킩��B���������āC
���̖Ԋ|�������ɂ�鉞����
��
�Ռ��Ƃ��Ď�舵���������Ƃ��킩��B���������āC
���̖Ԋ|�������ɂ�鉞����
�ł�������C����![]() �ȍ~�ɂ����O�͂���p���Ȃ������Ƃ����
�ȍ~�ɂ����O�͂���p���Ȃ������Ƃ����
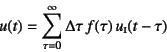
�����̉����ɂȂ邱�Ƃ͗����ł���Ǝv���B����������
![]() ��
�Ɍ����Ƃ邱�Ƃɂ���āC
��
�Ɍ����Ƃ邱�Ƃɂ���āC
 ��
�Ȃ�̂ŁC
�C�ӊO��
��
�Ȃ�̂ŁC
�C�ӊO��![]() �ɑ��鉞����
�ɑ��鉞����
�ƕ\���ł���B���̕\����Duhamel�ϕ�
�ƌĂ�ł���B���̉���![]() �ɂ�����돉�������̉��ɂȂ��Ă���B
���̂悤�ɁC�P�ʏՌ�����
�ɂ�����돉�������̉��ɂȂ��Ă���B
���̂悤�ɁC�P�ʏՌ�����
![]() �́C
�́C![]() ��
�S�̉����ɋy�ڂ��e���������Ă��邱�Ƃ���C
�ÓI�ȍ\���͊w�̉e�����Ɛ��w�I�ɂ͓������̂ł���B
������Green��
�ł���B
��
�S�̉����ɋy�ڂ��e���������Ă��邱�Ƃ���C
�ÓI�ȍ\���͊w�̉e�����Ɛ��w�I�ɂ͓������̂ł���B
������Green��
�ł���B
��Ƃ��āC�}-10.12�Ŏ�����![]() ��
����돉�������̉��������߂Ă݂悤�B�������͖ʓ|�Ȃ̂ŁC
���̏ꍇ���ɂ���ƁC���}�̉��ɂ��������C������
��
����돉�������̉��������߂Ă݂悤�B�������͖ʓ|�Ȃ̂ŁC
���̏ꍇ���ɂ���ƁC���}�̉��ɂ��������C������
�ł���B��(10.49)��
![]() �ł��邱�Ƃ�
��(10.48)�̒P�ʏՌ������Ƃ��������
�ł��邱�Ƃ�
��(10.48)�̒P�ʏՌ������Ƃ��������
�ƂȂ�BHeaviside������![]() �Ȃ̂ŁC
�Ȃ̂ŁC![]() �̐ϕ��͈͂�
�̐ϕ��͈͂�![]() �܂łɂȂ�B
����ɉ��Z�����
�܂łɂȂ�B
����ɉ��Z�����
�ƂȂ�̂ŁC���̐ϕ������s����Ή������߂���B
������ʓ|�Ȃ̂Ŋ������邪�C�ŏI�I�Ȍ��ʂ͏�̐����ƈ�v����B
�v�Z�ł�![]() ��
��![]() �̋�ʂ������ĊԈ��Ȃ��悤��!
�̋�ʂ������ĊԈ��Ȃ��悤��!
�O�̘͂A����![]() ��Z���ɐ������Ƃɕs�����o����l�̂��߂�
�ؖ����Ă������B
�Ȃ����̐߂́C�A�����J���B��Illinois�BEvanston,
Northwestern��wOlmstead����(1980�N�������j
��`Differential Equations of Mathematical Physics'��
�u�`�m�[�g���Q�l�ɂ����B������������
��Z���ɐ������Ƃɕs�����o����l�̂��߂�
�ؖ����Ă������B
�Ȃ����̐߂́C�A�����J���B��Illinois�BEvanston,
Northwestern��wOlmstead����(1980�N�������j
��`Differential Equations of Mathematical Physics'��
�u�`�m�[�g���Q�l�ɂ����B������������
�ł���B����C![]() �ɒP�ʏՌ��O�͂���p�����ꍇ��
�P�ʏՌ�����
�ɒP�ʏՌ��O�͂���p�����ꍇ��
�P�ʏՌ�����
![]() ��
����������B
��
����������B
������
![]() �͎�(10.43)��
��`����Dirac�̃f���^���ł���B
�͎�(10.43)��
��`����Dirac�̃f���^���ł���B
���ĖړI�́C![]() ��
��
![]() �ŕ\�����Ƃ����C
���̕⏕�̂��߂ɁC�P�ʏՌ���莮(
�ŕ\�����Ƃ����C
���̕⏕�̂��߂ɁC�P�ʏՌ���莮(![]() )��
�����������
�ƌĂ������`����B
�����l���͎��Ȑ����n�ł͂Ȃ����Ƃ���C
�������͎���
)��
�����������
�ƌĂ������`����B
�����l���͎��Ȑ����n�ł͂Ȃ����Ƃ���C
�������͎���![]() �ɒP�ʏՌ��O�͂�
��p�������̉���
�ɒP�ʏՌ��O�͂�
��p�������̉���
![]() �Ɋւ���I�ǒl���ɂȂ�C
�����ŗ^������B
�Ɋւ���I�ǒl���ɂȂ�C
�����ŗ^������B
�����ŁC�^���������̌������̕��������ɂȂ��Ă��邱�ƂƁC![]() �ł�
�I�Ǐ������^�����Ă��邱�Ƃɒ��ӂ���B
���̐������ƌ��̖��́u�ւ�肠���i���z�d���j�v���l���邽�߂ɁC
��(
�ł�
�I�Ǐ������^�����Ă��邱�Ƃɒ��ӂ���B
���̐������ƌ��̖��́u�ւ�肠���i���z�d���j�v���l���邽�߂ɁC
��(![]() )�̗��ӂ�
)�̗��ӂ�
![]() ���悶�Ď��Ԃ�
�ւ���
���悶�Ď��Ԃ�
�ւ���![]() ����
����![]() �܂Őϕ�����B
�����I�ɂ͉��z�d�������߂Ă��邱�ƂɂȂ�B
�܂Őϕ�����B
�����I�ɂ͉��z�d�������߂Ă��邱�ƂɂȂ�B
���̍��ӂ��ϕ������
�ƂȂ�B���̑�1���ɏ���������(![]() )��
�I�Ǐ�����(
)��
�I�Ǐ�����(![]() )�������C��2���̔�ϕ����̒��̊��ʕ�����
��(
)�������C��2���̔�ϕ����̒��̊��ʕ�����
��(![]() )�̉^�����������������
)�̉^�����������������
�ƂȂ�B
�Ō�̓����ł́C��(10.43)�̃f���^���̒�`��p�����B
���Ǐ㎮�����
�Ƃ����W��B���邢��![]() ��
��![]() �Ƃ����ւ����
�Ƃ����ւ����
�ƕ\�����B�ړI�Ɉ���ߕt���Ă���悤�Ɍ����邪�C �܂�``Close but no cigar!''�ł���B
���ɁC���l�́u�ւ�肠���i���z�d���j�v���C
�P�ʏՌ��̖��Ɛ������Ƃ̊Ԃōl�����
�ƂȂ邩��C��Ɠ��l�ɍ��ӂ��ϕ����āC�����E�I�Ǐ�����
��������������������ŁC�f���^���̒�`��p�����
�ƂȂ�B����C�㎮(![]() )�̉E�ӂ��f���^���̒�`��
�p�����
)�̉E�ӂ��f���^���̒�`��
�p�����
![]() �ƂȂ邩��C���ǁC��(
�ƂȂ邩��C���ǁC��(![]() )�����
)�����
�Ƃ����W��B�܂萏�����́C���̏Ռ����̊ϑ������ƍډ����� ����ւ��������̖��ł��邱�Ƃ��킩��B �×͊w�́u�����藝 �i��(3.73)�⎮(4.62)�j�v�Ɠ����ł���B
�ŏI�I�ɂ��̎�(![]() )����(
)����(![]() )�ɑ�������
)�ɑ�������
�ƂȂ�C![]() �͂ǂ�ȋL����p���Ă������ϕ��ϐ��ɉ߂��Ȃ�����
�͂ǂ�ȋL����p���Ă������ϕ��ϐ��ɉ߂��Ȃ�����
| (10.50) |
�ƁCDuhamel�ϕ����������邱�Ƃ��������Ƃ��ł����B
�Љ��Ս\���̐v�Ɋւ�������ł́C��q�̂悤�ɗL���v�f�@��
�p���āC�R���s���[�^�ɂ���ē��I��͂�����ꍇ������B
���̂Ƃ��̈�̉�͖@�ɁC����������
�ƌĂ����@�ŋߎ����C�����������ډ�����@������B
�����ł͒�������[8]�̍l�������ȒP�ɏq�ׂĂ����B
����́C�\�������Ȏ��ԃX�e�b�v![]() ���ɔ�����������������@�ł���B
�\�����ȒP�ɂ��邽�߂�
���ɔ�����������������@�ł���B
�\�����ȒP�ɂ��邽�߂�
�ƒ�`�����Ƃ��C����![]() �̑��x�Ɖ����x��
�̑��x�Ɖ����x��
�ŋߎ��ł���Ƃ���̂ł���B������^��������(10.16)�ɑ�������
�ƂȂ�̂ŁC���������
�Ƃ����W�����߂���B�܂�C����![]() ��
��![]() �̕ψ�
�̕ψ�![]() ��
��![]() ��
�킩���Ă���C���̎����玞�X���X�̉������ɋ��߂邱�Ƃ��ł���B
��
�킩���Ă���C���̎����玞�X���X�̉������ɋ��߂邱�Ƃ��ł���B
�������C��ԍŏ��̃X�e�b�v��![]() �����Ȃ̂���`�ł��Ă��Ȃ���ɁC
���������̂����̏��������͂ł��Ă��Ȃ��B������
�Ⴆ�Ύ���
�����Ȃ̂���`�ł��Ă��Ȃ���ɁC
���������̂����̏��������͂ł��Ă��Ȃ��B������
�Ⴆ�Ύ���![]() ������ލ�����
������ލ�����
����![]() ���T�Z���邱�Ƃ��\�����C�����̎����ɐ������������Ȃ�B
�����ł���ɂ��ẮC
��(10.51)�̓�̎�����
���T�Z���邱�Ƃ��\�����C�����̎����ɐ������������Ȃ�B
�����ł���ɂ��ẮC
��(10.51)�̓�̎�����![]() ���������ē���
���������ē���
������![]() �ŕ\�����C�����
�ŕ\�����C�����![]() �̏u�Ԃ̉^�����������瓾��
�̏u�Ԃ̉^�����������瓾��
�Ƃ����W����̎��̉E�ӑ�3���ɑ�������
�ƂȂ邱�Ƃ���C
����![]() ��
��![]() ���Z��ł��C���������͂ł���B
���Z��ł��C���������͂ł���B![]() �ŗ돉�������ł���C
����
�ŗ돉�������ł���C
����
![]() �ł����B
���Ƃ��āC�}-10.12��
�����������������ʂ�}-10.18�Ɏ������B
�قƂ�Ǐd�Ȃ��Č����Ȃ����C
�}���̔j�����������Ȃ̂ŁC
�ł����B
���Ƃ��āC�}-10.12��
�����������������ʂ�}-10.18�Ɏ������B
�قƂ�Ǐd�Ȃ��Č����Ȃ����C
�}���̔j�����������Ȃ̂ŁC
![]() �ɂ�������������
�\���Ȑ��x�������Ă��邱�Ƃ��킩��B����ɑ��C
�ɂ�������������
�\���Ȑ��x�������Ă��邱�Ƃ��킩��B����ɑ��C
![]() �Ƃ���
���ʂׂ̍������͌���������̂��ꂪ���ԂƋ��Ɏ���ɑ傫���Ȃ�B
�Ƃ���
���ʂׂ̍������͌���������̂��ꂪ���ԂƋ��Ɏ���ɑ傫���Ȃ�B
�}-10.19�ɂ͌v�Z�̃t���[�`���[�g��
�������B�܂��}-10.20�ɂ́C�}-10.8��
���肵���o�l�̊��n�k�����x�ŗh�炵���Ƃ��̐��l��͌��ʁi�����j��
�������ʁi�j���j�̂����C�����O�͂��傫�����ԑт̕����������������B
���͒n�k�g�́C���Ɍ��암�n�k�̐_�ˊC�m�C�ۑ�Ŋϑ����ꂽ
�����x�̔����ł��邪�C���̒��x�̐��x�Ő��l��͂��ł���B
���̂悤�Ȑϕ����@���z��@
�ƌĂ�ł���B��ʂɒ��������ɂ�鐔�l�ϕ��́u���萫�v�̂��߂ɂ́C
���ԃX�e�b�v�͎�����
![]() ��菬�����Ȃ���
�����Ȃ�[8]�Ƃ����B�}-10.18��
�ŏ��̗�ł́C����������������
��菬�����Ȃ���
�����Ȃ�[8]�Ƃ����B�}-10.18��
�ŏ��̗�ł́C����������������![]() ��
������7���x�Ȃ̂ŁC
��
������7���x�Ȃ̂ŁC
![]() �͈��萫�ɂ͏\���ŁC
��͂͌p���ł��Ă��邪�C�u���m���v�ɂ��Ă͂����Ə�����
���ԃX�e�b�v���K�v���Ƃ������Ƃ������Ă���B
�͈��萫�ɂ͏\���ŁC
��͂͌p���ł��Ă��邪�C�u���m���v�ɂ��Ă͂����Ə�����
���ԃX�e�b�v���K�v���Ƃ������Ƃ������Ă���B
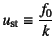 ��
�����Ƃ���
��
�����Ƃ���
�ƕ\�����Ƃ��ł��邱�Ƃ�p���C�܂�Duhamel�ϕ��� ��(10.47)�̂悤��Heaviside�����܂܂܂� �P�ʏՌ�������p���Čv�Z����ƁC�ꍇ�����������ɁC�y�� �ԈႢ�������邱�Ƃ��ł���B
���߂̕s�K����������舵�����߂�
�K�v�Ȃ��̂����C
![]() ��
�����O�͂ɑ��鉞���i���f�����ƌĂԁj���l���Ă݂�B���邢��
��
�����O�͂ɑ��鉞���i���f�����ƌĂԁj���l���Ă݂�B���邢��
�ł��邩��C�����g�����Ɨ]���g�������ɋ��߂悤�Ƃ��Ă���ƍl���Ă������B
����ɑ��鉞�������l��
![]() ��
�u�����Ƃ��ł��������B
��
�u�����Ƃ��ł��������B![]() ��
���f���ł���B������^��������(10.16)�ɑ�������
��
���f���ł���B������^��������(10.16)�ɑ�������
�ƂȂ�̂�
�Ƌ��߂���B�����ł́C![]() ��p�����B���������ĕ��f������
��p�����B���������ĕ��f������
�ƕ\�����Ƃ��ł���B����������
![]() �́C�P�ʂ̎����O�͂ɑ���
�����̐U���ł��邱�Ƃ���C���g���i�U�����j������
�ƌĂ��B
���̊��̋��������C��-10.1.3 (1)��
���߂������g�����ɂȂ��Ă���B
�́C�P�ʂ̎����O�͂ɑ���
�����̐U���ł��邱�Ƃ���C���g���i�U�����j������
�ƌĂ��B
���̊��̋��������C��-10.1.3 (1)��
���߂������g�����ɂȂ��Ă���B
![]() �̕��̕Ίp��
�̕��̕Ίp��![]() �Ƃ����
�Ƃ����
�Ə������Ƃ��ł�
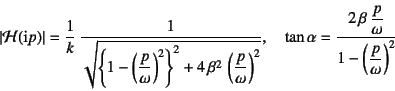
�ƂȂ邩��C��(10.35b)�Ɣ�r����Ζ��炩�Ȃ悤�ɁC
���I������![]() �Ƃ̊W��
�Ƃ̊W��
�ł���C![]() �͎�(10.35c)�Œ�`���ꂽ�ʑ��̒x��ł���B
�͎�(10.35c)�Œ�`���ꂽ�ʑ��̒x��ł���B
��-10.1.3 (2)�Ŏ������x�_��
�����I�ɕψʂ������ꍇ�����l��
�Ƃ����
�Ƌ��߂���̂ŁC�x�_�Ƃ̑��Εψʂ�
�ƂȂ�C
![]() �ł���B
�ł���B
���āC![]() �̒P�ʂ̎����O�͂ɑ��鉞���́C��(10.56)����
�̒P�ʂ̎����O�͂ɑ��鉞���́C��(10.56)����
�ƂȂ�B�������́CDuhamel�ϕ���p���Ă����߂邱�Ƃ��ł���͂����B
�����ł́C![]() �ɉ��炩�̏����������^�����āC
����ȍ~�p�����ĐU���������Ă�����̂ƍl���悤�B
�܂�
�ɉ��炩�̏����������^�����āC
����ȍ~�p�����ĐU���������Ă�����̂ƍl���悤�B
�܂�
![]() ��������Duhamel�ϕ���
��������Duhamel�ϕ���
�Ə������Ƃ��ł���B������![]() �Ƃ����ϐ��ϊ���
����ƁC
�Ƃ����ϐ��ϊ���
����ƁC
![]() ,
,
![]() �Ȃ̂ŏ㎮��
�Ȃ̂ŏ㎮��
�Ə����������Ƃ��ł���B���̍Ō�̕\���Ə�̎�(![]() )���r�����
)���r�����
�Ƃ����W�ɂ��邱�Ƃ��킩��B���Ȃ킿�C���g��������
![]() ��
�P�ʏՌ�����
��
�P�ʏՌ�����![]() ��Fourier�ϊ�(
F)�Ȃ̂��BFourier�ϊ�
�ɂ��Ă͐�-10.1.4 (1)��
��������B���������āC�������S���قȂ�ƍl����ꂻ���ȓ�̉����C
�܂�����O�͂ɑ��鉞���ƒP�ʏՌ������Ƃ̊Ԃɂ�
��(10.60)�̊W�C���邢��
��Fourier�ϊ�(
F)�Ȃ̂��BFourier�ϊ�
�ɂ��Ă͐�-10.1.4 (1)��
��������B���������āC�������S���قȂ�ƍl����ꂻ���ȓ�̉����C
�܂�����O�͂ɑ��鉞���ƒP�ʏՌ������Ƃ̊Ԃɂ�
��(10.60)�̊W�C���邢��
�Ƃ����W�����݂��邱�Ƃ����炩�ɂȂ����B ����͂�����Ɩʔ�������܂��B �Ƃ����̂��C�Ռ������ɂ͎����^���̗v�f�͊܂܂�Ă��Ȃ��悤�� �����邩�炾�B �������t�ɁC��̊W������т��̗U����������炩�Ȃ悤�ɁC �Ռ������͂��ׂĂ̎��g���̉������ϓ��Ɋ܂�ł���̂ł���B
�O�̐߂܂ł́C��X�̐}�̉����ɂ͎���![]() ���Ƃ��Ă����B
�������C�Ⴆ�ΈقȂ�����ɓ������f�w�Ŕ���������̒n�k�g���C
�����n�Ղ��o�ē��B�����ꍇ�C���̎��Ԏ���̉����x�g�`���́u�������v��
�����ɂ͂Ȃ�Ȃ����Ƃ͗e�Ղɗ\�z�����B
����́C�f�w��̔j��̍L������������X�قȂ邩�炩������Ȃ��B
�������C�������f�w���瓯���n�Ղ��o����̔g�̎������̈�C
�u���g�������̕��z�v�ɂ́C���܂�Ⴂ�͖����̂ł͂Ȃ����낤���ƁC
���҂��Ă���B
���̂��߁C�����Ɏ��g�����Ƃ����}�Őv�����邱�Ƃ��l���悤�B
���̂悤�ȁC�����Ɏ��g�����Ƃ������̂œǎ҂����ɒm���Ă����
�v������̂̑�\��Fourier�W�����낤�B
��������Fourier�����́C�ő����
���Ƃ��Ă����B
�������C�Ⴆ�ΈقȂ�����ɓ������f�w�Ŕ���������̒n�k�g���C
�����n�Ղ��o�ē��B�����ꍇ�C���̎��Ԏ���̉����x�g�`���́u�������v��
�����ɂ͂Ȃ�Ȃ����Ƃ͗e�Ղɗ\�z�����B
����́C�f�w��̔j��̍L������������X�قȂ邩�炩������Ȃ��B
�������C�������f�w���瓯���n�Ղ��o����̔g�̎������̈�C
�u���g�������̕��z�v�ɂ́C���܂�Ⴂ�͖����̂ł͂Ȃ����낤���ƁC
���҂��Ă���B
���̂��߁C�����Ɏ��g�����Ƃ����}�Őv�����邱�Ƃ��l���悤�B
���̂悤�ȁC�����Ɏ��g�����Ƃ������̂œǎ҂����ɒm���Ă����
�v������̂̑�\��Fourier�W�����낤�B
��������Fourier�����́C�ő����![]() �Ƃ������̂�����M���̏�����
�O��Ƃ������U�I�Ȏ��g�������������B
����ɑ��C�Ⴆ�Βn�k�g�̋L�^������Ζ��炩�Ȃ悤�ɁC
���̂悤�ȕs�K���M���ɂ͍ő����
�Ƃ������̂�����M���̏�����
�O��Ƃ������U�I�Ȏ��g�������������B
����ɑ��C�Ⴆ�Βn�k�g�̋L�^������Ζ��炩�Ȃ悤�ɁC
���̂悤�ȕs�K���M���ɂ͍ő����![]() �Ƃ������̂������B
���邢�́C�����
�Ƃ������̂������B
���邢�́C�����![]() �ƍl���Ȃ���Ȃ�Ȃ��Ƃ������ƂɂȂ�B
������Fourier��������c�_���n�߁C���̍ő��������ɂƂ����Ƃ���
�������Љ�C�����p�����v�@�ɂ��ĊȒP�ɏq�ׂĂ������B
�ƍl���Ȃ���Ȃ�Ȃ��Ƃ������ƂɂȂ�B
������Fourier��������c�_���n�߁C���̍ő��������ɂƂ����Ƃ���
�������Љ�C�����p�����v�@�ɂ��ĊȒP�ɏq�ׂĂ������B
���āC�O��![]() �Ƃ������̂قƂ�ǂ��ߎ��I�ɁC
�ő����
�Ƃ������̂قƂ�ǂ��ߎ��I�ɁC
�ő����![]() ��Fourier������
��Fourier������
�ƕ\���Ă��������Ƃ́C�����m���Ă���Ǝv���B
������![]() �͍ŏ��U����
�͍ŏ��U����
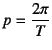 �ł���B
�������(10.56) (10.57)��p����������
�������ƁC
�ł���B
�������(10.56) (10.57)��p����������
�������ƁC![]() ���ȗ����đ�G�c�ɂ�
���ȗ����đ�G�c�ɂ�
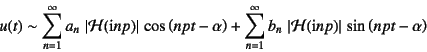
�ƂȂ邱�Ƃ���
�Ƃ����W�����藧���ƂɂȂ�B
�Ⴆ�ΊO�͂�Fourier�W���̐�Βl�́C
�O�͂̒���![]() (
(
![]() )�̎��g�������́u�����v��\���Ă���B
�Љ��Ս\����v����
)�̎��g�������́u�����v��\���Ă���B
�Љ��Ս\����v����![]() ��ݒ肵�C
�O�͂�Fourier�W��������ɏ悶�ĉ�����Fourier�W���̐�Βl�����߂��C
�����̒���
��ݒ肵�C
�O�͂�Fourier�W��������ɏ悶�ĉ�����Fourier�W���̐�Βl�����߂��C
�����̒���![]() �̎��g�������́u�����v�����߂���B
�����C���̉����́u�����v���C�ޗ���\������R�ł���u�����v����
�傫���Ȃ��Ă��܂��ƁC���̍\���͔j�Ă��܂����ƂɂȂ�B
�܂�C�Ⴆ�Βn�k�̊O�͂�O���ɒu�����Ƃ��C�}-10.22��
�������悤�ɁC�\����n�Ղ͊O�͐M������������t�B���^�[�̖�ڂ�
���Ă��āC����I�ɐv����ۂɂ́C���̉�����Fourier�W���i���
�E�̐}�j������̑傫�����Ȃ��悤�ɁC�ޗ���\���C
�܂�
�̎��g�������́u�����v�����߂���B
�����C���̉����́u�����v���C�ޗ���\������R�ł���u�����v����
�傫���Ȃ��Ă��܂��ƁC���̍\���͔j�Ă��܂����ƂɂȂ�B
�܂�C�Ⴆ�Βn�k�̊O�͂�O���ɒu�����Ƃ��C�}-10.22��
�������悤�ɁC�\����n�Ղ͊O�͐M������������t�B���^�[�̖�ڂ�
���Ă��āC����I�ɐv����ۂɂ́C���̉�����Fourier�W���i���
�E�̐}�j������̑傫�����Ȃ��悤�ɁC�ޗ���\���C
�܂�![]() ��
��![]() ���邢��
���邢��![]() ��K�ɐv����������ƂɂȂ�B
�ȉ��C�����������J�ɁC�������V����I�ɐ������Ă������B
��K�ɐv����������ƂɂȂ�B
�ȉ��C�����������J�ɁC�������V����I�ɐ������Ă������B
���āC��(10.61)��Euler�̌���
��p����10.8���������
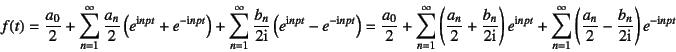
�ƕ\�����Ƃ��ł���B�����Ŏ�(10.61)��p����ƁC![]() ���܂߂�
���܂߂�
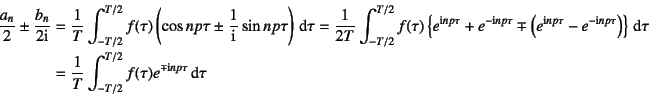
�ƂȂ�̂ŁC�㎮�ɑ����������
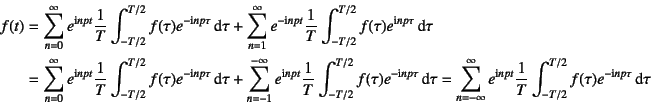
�Ƃ����\���ɂȂ�B��������fFourier���� �ƌĂ�C����
(10.62)
�ƕ\�����Ƃ��ł���B![]() �͕��fFourier�W���ƌĂ��B
�͕��fFourier�W���ƌĂ��B
�����ď������\�ȉ��Z�����邪�C
������
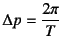 ,
, ![]() �ƒu���ƁC
�㎮(10.63b)��
�ƒu���ƁC
�㎮(10.63b)��![]() ����(10.63a)��
�����\���ɑ���������̂�
����(10.63a)��
�����\���ɑ���������̂�
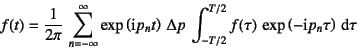
�Ə������Ƃ��ł���B
������![]() �Ƃ��邱�Ƃɂ���āC
�Ƃ��邱�Ƃɂ���āC![]() ,
,
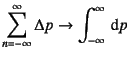 ��
�u������������̂Ƃ�����ŁC
��
�u������������̂Ƃ�����ŁC![]() �𗣎U�ʂ���A���ʂɕύX����
�𗣎U�ʂ���A���ʂɕύX����![]() ��
�u�������C�㎮��
��
�u�������C�㎮��
�ƂȂ�̂ŁC����
(10.63)
�Ƃ����W��B��(10.64b)��
��![]() ��Fourier�ϊ�
�ł���C��(10.64a)��Fourier�t�ϊ��ł���B
�Ȃ��C�w�����̕������t�ɒ�`����Ă���ꍇ��C
�t�ϊ��̐ϕ��̑O������
��Fourier�ϊ�
�ł���C��(10.64a)��Fourier�t�ϊ��ł���B
�Ȃ��C�w�����̕������t�ɒ�`����Ă���ꍇ��C
�t�ϊ��̐ϕ��̑O������
![]() �Ƃ������ɁC
�����̐ϕ��̑O��
�Ƃ������ɁC
�����̐ϕ��̑O��
![]() �Ƃ��Ē�`����ꍇ������̂�
���ӂ��ė~�����B
������ɂ��Ă������I�ȈӖ��͕ς��Ȃ��B
�Ƃ��Ē�`����ꍇ������̂�
���ӂ��ė~�����B
������ɂ��Ă������I�ȈӖ��͕ς��Ȃ��B
���f�����o�Ă����肵��Fourier�ϊ��ƕ����������Ŗ킩��Ȃ��Ȃ邩��
����Ȃ����C���傤�ǐ}-10.22�̍�����![]() ��Fourier�W����
���z�̂悤�ɁC����Fourier�ϊ��́u�l�v�́C
����M��
��Fourier�W����
���z�̂悤�ɁC����Fourier�ϊ��́u�l�v�́C
����M��![]() �Ɋ܂܂�鐬���̑傫����
�A���I�Ȏ��g�����ɕ\���Ă���ƍl��������B
������Fourier�ϊ��Ƃ����u����v�́C���傤�nj��̕����̃v���Y���̖�����
�������ƍl��������B
�v���Y���ɔ��F���Ă�ƁC�g����700nm���炢�̐ԁi���g���̋t����
�����Ɋ��Z�����
�Ɋ܂܂�鐬���̑傫����
�A���I�Ȏ��g�����ɕ\���Ă���ƍl��������B
������Fourier�ϊ��Ƃ����u����v�́C���傤�nj��̕����̃v���Y���̖�����
�������ƍl��������B
�v���Y���ɔ��F���Ă�ƁC�g����700nm���炢�̐ԁi���g���̋t����
�����Ɋ��Z�����
![]() s���炢�j����C
�g����300nm���炢�̎��i������
s���炢�j����C
�g����300nm���炢�̎��i������
![]() s���炢�j��
�����ɕ������ĖڂŌ��邱�Ƃ��ł���B
�n�k�����x��\���̕s�K���������C���傤�ǐ}-10.23��
�E���Ɏ������悤�ɁCFourier�ϊ��Ƃ����v���Y����ʂ��āC
�Ⴆ�ΎЉ��Ս\���ɂƂ��ďd�v��1s���炢�܂ł̎����������ɕ�������
��舵�����Ƃ��Ă���ƍl����C�����͗������i�ނ�������Ȃ��B
s���炢�j��
�����ɕ������ĖڂŌ��邱�Ƃ��ł���B
�n�k�����x��\���̕s�K���������C���傤�ǐ}-10.23��
�E���Ɏ������悤�ɁCFourier�ϊ��Ƃ����v���Y����ʂ��āC
�Ⴆ�ΎЉ��Ս\���ɂƂ��ďd�v��1s���炢�܂ł̎����������ɕ�������
��舵�����Ƃ��Ă���ƍl����C�����͗������i�ނ�������Ȃ��B
�s�K�������̑�\��͒n�k�����ł���B�n�k�g���̂��̂��s�K���M���ł��낤�B
����������v�ʂƂ��Ă̕��ϒl�͗�Ȃ̂ŁC���܂�S�͖����B
����������̂͗͂≞���́u�����v�ł��邩��C�U����2��C���邢��
���U���d�v�ȓ��v�ʂł��낤�B�����Ŋe�핶��������ƁC�Ⴆ��
�O��![]() �̕��U��
�̕��U��
�ƒ�`���Ă������炵���B
������![]() ��
��![]() ��Fourier�ϊ��ł���B
���̔�ϕ�����
��Fourier�ϊ��ł���B
���̔�ϕ�����
�ƋL���C![]() ���p���[�X�y�N�g�����x��
�ƌĂԁB�Ⴆ��
���p���[�X�y�N�g�����x��
�ƌĂԁB�Ⴆ��
����Ԃ킩��Ղ���ł���B
���Ȃ݂�
![]() ��Fourier�X�y�N�g��
�ƌĂ�ł���B
��Fourier�X�y�N�g��
�ƌĂ�ł���B
����ɑ��C����O��![]() �́C����
�́C����![]() �������ꂽ�����M���Ƃ�
�ς̊��Ғl
�������ꂽ�����M���Ƃ�
�ς̊��Ғl
�����ȑ��֊�
�ƌĂԁB![]() ���������Ȃ�C
���������Ȃ�C![]() �������̔{���̂Ƃ���
�ł����ւ������Ȃ邱�Ƃ���C���̎��ȑ��֊������炩�̎���������
�\�����Ă��邱�Ƃ��\�z�����B���Ȃ݂�
�������̔{���̂Ƃ���
�ł����ւ������Ȃ邱�Ƃ���C���̎��ȑ��֊������炩�̎���������
�\�����Ă��邱�Ƃ��\�z�����B���Ȃ݂�
�ł���B���̎��ȑ��֊���Fourier�ϊ������
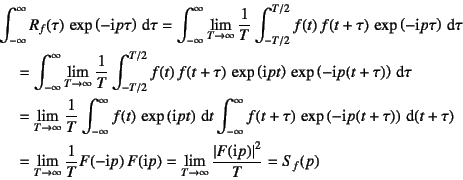
�̂悤�ɁC�p���[�X�y�N�g�����x���ɂȂ�B
�܂�
�Ƃ����W���������C�����Wiener-Khintchine�̊W10.9 �ƌĂ�ł���B
�ł́C�s�K���ȊO�͂ɑ���ψʉ��������߂悤�B
���Ԏ��ɂ����鎞�������������߂����Ȃ�Duhamel�ϕ���
���l��@��p��������B�������O�q�̂悤�ɁC�s�K���O�͂�
���鉞�����s�K���ł���C��͂���g���̊��Ƃ��Ď�舵��������
�����I�ɂ͈Ӗ������肻�����B
�����ł́C���̔c���̕��@�������Ă����B1���R�x�n��
����![]() �̎��ȑ��֊����C�O�͂̏ꍇ�Ɠ��l
�̎��ȑ��֊����C�O�͂̏ꍇ�Ɠ��l
�ƒ�`����B�����Duhamel�ϕ���
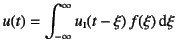 ��
��������
��
��������
�Ə������Ƃ��ł���B
������![]() ,
,
![]() �Ƃ����ϐ��ϊ��������
�Ƃ����ϐ��ϊ��������
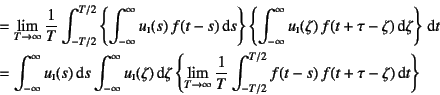
�����![]() �̕ϐ��ϊ�������ƁC
�̕ϐ��ϊ�������ƁC![]() �̎��ȑ��֊�������
�̎��ȑ��֊�������
�ƂȂ�B
�ŏI�I�ɉ����̃p���[�X�y�N�g�����x���́C
�㎮�̎��ȑ��֊���Fourier�ϊ�����
�Ƃ����\���ɂȂ�B�����ŕϐ��ϊ���
![]() �Ƃ����
�Ƃ����
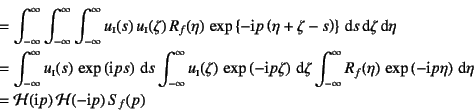
�ƂȂ�̂ŁC����
�Ƃ����W�����߂���B���邢�͎�(10.58)��p�����
�Ƃ����W�ɂ��邱�ƂɂȂ�B���������āC![]() ������white noise��
�\���ɍ�p�����ē��邱�Ƃ��ł��鉞���̃p���[�X�y�N�g�����x��
������white noise��
�\���ɍ�p�����ē��邱�Ƃ��ł��鉞���̃p���[�X�y�N�g�����x��![]() �́C
���̂܂܋��U�Ȑ��i��2��j�ɑ������邱�ƂɂȂ�B
�Ⴆ�ΎЉ��Ս\���Ŋϑ������^�钆�̔���ȐU���i�펞�����ƌĂԁj��
���肷��C����͂قƂ��white noise�̂悤�ȕ��̍L�����g���т�
�����p���[���������O�́i���ӊ�����`����Ă����X�G���ȓ��I��p�j
�ɑ��鉞�����Ƌߎ����Ă����̂ŁC
���̃f�[�^�����U�Ȑ��܂���g���������̐�Βl�ɑ�������B
�́C
���̂܂܋��U�Ȑ��i��2��j�ɑ������邱�ƂɂȂ�B
�Ⴆ�ΎЉ��Ս\���Ŋϑ������^�钆�̔���ȐU���i�펞�����ƌĂԁj��
���肷��C����͂قƂ��white noise�̂悤�ȕ��̍L�����g���т�
�����p���[���������O�́i���ӊ�����`����Ă����X�G���ȓ��I��p�j
�ɑ��鉞�����Ƌߎ����Ă����̂ŁC
���̃f�[�^�����U�Ȑ��܂���g���������̐�Βl�ɑ�������B
���Ȃ킿�C�O�͂̃p���[�X�y�N�g�����x�����^����ꂽ�Ƃ��C
���̎�(10.70)�ŋ��߂��鉞���̃p���[�X�y�N�g�����x����
����̏���������悤�Ɂi�\�����j�Ȃ��悤�Ɂj�C
�\����ޗ���I������
![]() ��
�v����������ƂɂȂ�B�}-10.22�ł�Fourier������
�p���Ă����̂ŁC�X�y�N�g����
��
�v����������ƂɂȂ�B�}-10.22�ł�Fourier������
�p���Ă����̂ŁC�X�y�N�g����![]() ���݂ɕ\�����ꂽ���U�I�Ȃ��̂ł������̂ɑ��C
�O�͂��̂��̂ɍő�����Ƃ������̂���`�ł��Ȃ��n�k�O�͂̂悤��
�s�K���O�͂Ƃ��̉�������������ꍇ�ɂ́C�}-10.24��
�悤�ɘA���I�Ȏ��g���Ŋ��\�����ꂽ
���݂ɕ\�����ꂽ���U�I�Ȃ��̂ł������̂ɑ��C
�O�͂��̂��̂ɍő�����Ƃ������̂���`�ł��Ȃ��n�k�O�͂̂悤��
�s�K���O�͂Ƃ��̉�������������ꍇ�ɂ́C�}-10.24��
�悤�ɘA���I�Ȏ��g���Ŋ��\�����ꂽ![]() ,
, ![]() �Ƃ�����
�A���X�y�N�g����p����̂ł���B
���̐}�̂悤�ȏꍇ�ɂ́C�vB�̕����]�܂����ƍl���Ă������낤�B
�Ƃ�����
�A���X�y�N�g����p����̂ł���B
���̐}�̂悤�ȏꍇ�ɂ́C�vB�̕����]�܂����ƍl���Ă������낤�B
�ϐk�v�̂��Ƃ��Ō�ɍl���Ă����B��(10.38)�ɂ���悤�ɁC
�O�͂͒n�k�����x�Ɏ��ʂ��悶�����̂ł���B
�܂�C�O�߂�![]() �ɂ́C�W���I�Ȓn�k�����x
�ɂ́C�W���I�Ȓn�k�����x![]() ��
��![]() ��
���ē��͂�������悤��
�v���邪�C���ۂɂ͂����Ȃ��Ă��Ȃ��B����[129]��
�߂ɓǂނƁC����ŗL�U�����i�����j������1���_�n�ɕW���I��
�n�k�����x����͂��ē��邱�Ƃ��ł���u��Ή����x����
��
���ē��͂�������悤��
�v���邪�C���ۂɂ͂����Ȃ��Ă��Ȃ��B����[129]��
�߂ɓǂނƁC����ŗL�U�����i�����j������1���_�n�ɕW���I��
�n�k�����x����͂��ē��邱�Ƃ��ł���u��Ή����x����![]() �v��
�ő�l���C��ɗ^������͒n�k�����x�ɂ���Ƃ��Ă���B
�Ȃ�ƂȂ���������@�́i�ہC���㉮���˂��C
���邢�͖��łɈ��S���m�ۂ��悤�Ƃ���j�悤�ő�1���҂ɂ͗����ł��Ȃ����C
�\���̉ߓn���������܂߂ēK�ȓ��͉����x�����߂邽�߂Ƃ���Ă���B
�v��
�ő�l���C��ɗ^������͒n�k�����x�ɂ���Ƃ��Ă���B
�Ȃ�ƂȂ���������@�́i�ہC���㉮���˂��C
���邢�͖��łɈ��S���m�ۂ��悤�Ƃ���j�悤�ő�1���҂ɂ͗����ł��Ȃ����C
�\���̉ߓn���������܂߂ēK�ȓ��͉����x�����߂邽�߂Ƃ���Ă���B
�܂�Duhamel�ϕ��\���Ɏ�(10.47)�̒P�ʏՌ��������������
�ƕψʂ��\�����B�����![]() �Ŕ��������
�Ŕ��������
![\begin{eqnarray*}
\dot{u}&=&\int_0^\infty
\dfrac{f(\tau)}{m \omega_d}e^{-\beta...
..._d(t-\tau)\}
+\omega_d \cos\{\omega_d(t-\tau)\}
\right]\dint\tau
\end{eqnarray*}](s4img450.gif)
�ƕ\�����B��ϕ����̑�2���́C�f���^���̒�`�����ɂȂ�B
������^���������ɑ������Ή����x�����߂��邪�C
�����ł͍ēx![]() �Ŕ��������
�Ŕ��������
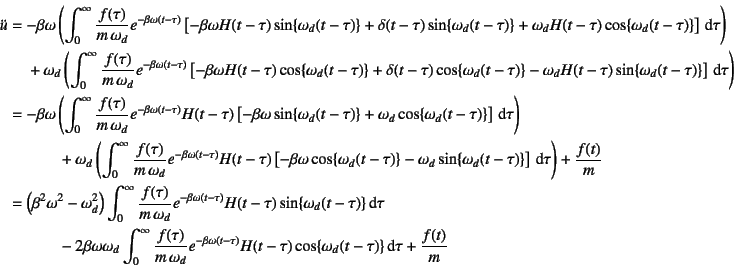
�ƂȂ�B�����Ɏ�(10.37)����![]() �ɕύX���C
��(10.38)����
�ɕύX���C
��(10.38)����
![]() ���������
���������
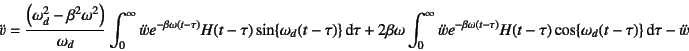
�ƂȂ�B�ēx��(10.37)��p����C��Εψʂ̉����x��
�ƕ\�����Ƃ��ł���B������
�ƒ�`�����B���������āC�����x�����̃X�y�N�g�����x����
�Ƃ����W�ɂȂ�B������![]() ��1���_�n�̉����x����
��1���_�n�̉����x����![]() ��
�X�y�N�g�����x���ŁC
��
�X�y�N�g�����x���ŁC![]() �͂���1���_�n��
���ۂɗ^�������͒n�k�����x
�͂���1���_�n��
���ۂɗ^�������͒n�k�����x![]() �̃X�y�N�g�����x���ł���B
�̃X�y�N�g�����x���ł���B
�����Ō��ϐk�v�@�ł́C����W���I�Ȑv�p�̓��͒n�k�����x![]() ���C
��X�̌ŗL�����i�U�����j
���C
��X�̌ŗL�����i�U�����j![]() ,
, ![]() etc.��
����1���R�x�n�ɓ��͂��āC��(10.73)��
�����x���������߂�B���̍ő�l
etc.��
����1���R�x�n�ɓ��͂��āC��(10.73)��
�����x���������߂�B���̍ő�l
![]() ���C
���̑Ή������ŗL�����i�U�����j��
���\���ɑ�����͒n�k�Ƃ��āC���̍\���̊�ɗ^���邱�ƂɂȂ��Ă���B
�l�������ȒP�ɐ}-10.25�Ɏ������B
����[129]�ɂ́C�����x�̒P�ʂł���
�ő�l
���C
���̑Ή������ŗL�����i�U�����j��
���\���ɑ�����͒n�k�Ƃ��āC���̍\���̊�ɗ^���邱�ƂɂȂ��Ă���B
�l�������ȒP�ɐ}-10.25�Ɏ������B
����[129]�ɂ́C�����x�̒P�ʂł���
�ő�l
![]() ���^��������B
�Ⴆ��1���R�x�n��v����ꍇ�ɂ́C
�v���ē���
���^��������B
�Ⴆ��1���R�x�n��v����ꍇ�ɂ́C
�v���ē���![]() �ŌŗL����
�ŌŗL����![]() �����߁C
���̉E�̐}���炻��
�����߁C
���̉E�̐}���炻��![]() �̒l�ɑΉ�����
�ő�����x����
�̒l�ɑΉ�����
�ő�����x����
![]() �����߂�B
�����āC
�v���ē�������
�����߂�B
�����āC
�v���ē�������![]() ������ɏ悶��
������ɏ悶��
![]() ��
���̎��_�ɊO�͂Ƃ��č�p�������Ƃ��̃o�l�̒�R�͂��Z�肵�C
���ꂪ�j�Ȃ����x���ɂ��邩�ǂ������m���߂�̂ł���B
��
���̎��_�ɊO�͂Ƃ��č�p�������Ƃ��̃o�l�̒�R�͂��Z�肵�C
���ꂪ�j�Ȃ����x���ɂ��邩�ǂ������m���߂�̂ł���B