- ... (固有振動数)\fakejchar10.1
- 正確には固有円振動数
あるいは固有角振動数
と呼ぶが,以下,省略して単に固有振動数と呼ぶことにする。
真の固有振動数
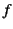 は固有周期の逆数で
は固有周期の逆数で
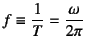 (単位は1/sあるいはHz)で定義される。
(単位は1/sあるいはHz)で定義される。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...減衰定数10.2
- 多分道路橋示方書[129]で使っているからだと思うが,
最近は
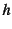 を使う書籍や論文が多いようである。
しかしここでは,最も基本的で重要な物理パラメータの振動数
を使う書籍や論文が多いようである。
しかしここでは,最も基本的で重要な物理パラメータの振動数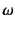 と
揃えるためだけの理由でギリシャ文字
と
揃えるためだけの理由でギリシャ文字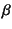 を用いている。
を用いている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (減衰比)\fakejchar10.3
- 教科書によってはこれを減衰率
と呼び,また別の教科書には
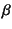 を減衰比とするものがあるので,
注意すること。
を減衰比とするものがあるので,
注意すること。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
)が発生する床の上の振動10.4
- 実際には,バネが伸び切って振動が止まる瞬間の摩擦力は最大摩擦力
程度以下の静止摩擦抵抗でいいわけだが,
ここでは簡単のために動摩擦力のみで近似する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...と書く10.5
- あるいは,後述の式(10.46)で
定義するHeavisede関数を用いて
と書いてもいい。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...の状態10.6
- 正確には,静止摩擦係数
を
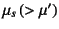 とした場合,
速度が零になった瞬間には最大摩擦力
程度以下の静止摩擦抵抗
とした場合,
速度が零になった瞬間には最大摩擦力
程度以下の静止摩擦抵抗
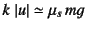 のときに
止まるので,
のときに
止まるので,
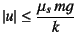 で
止まることになる。
で
止まることになる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
であるから,工学的に一番興味があるのは特解の方10.7
- 演習問題を解けばわかるはずだが,実際には,過渡応答を含めた
振幅が動的増幅率を超えることがあることには注意するべきである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...を用いて10.8
- ある映画で有名になったが,
五つの基本量間の式`
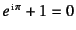 'は
確かに驚くべき関係ではないだろうか。
'は
確かに驚くべき関係ではないだろうか。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Wiener-Khintchineの関係10.9
- 文献によっては,Khinchin[e]という表記もある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...と表現10.10
- 常に
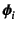 の第1成分が非零とは限らないので注意する。
第1著者はときどきそういう問題を定期試験に出すことがある。
の第1成分が非零とは限らないので注意する。
第1著者はときどきそういう問題を定期試験に出すことがある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...が10.11
- この式は厳密ではないが,社会基盤構造のモデルとして
用いられる実際の細長い梁に対しては,それほど精度は悪くない。
回転運動の運動方程式を正しく定式化した
理論については節-10.4.8 (1)を
参照のこと。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
講義ノート10.12
- よく理解できなかったので,単位は取得していない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...座標10.13
- これを見て,
いわゆる均質化法[113]を思い浮かべた人は勘がいい。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...という独立変数10.14
- あるいは後述のように,座標
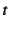 のスケールを
のスケールを
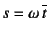 ,
,
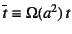 のように変更したと考えてもいい。
こう考えた方が,前の節で代数方程式に対して導入した特異摂動法の
スケールの変更式(10.258)と
整合する。
のように変更したと考えてもいい。
こう考えた方が,前の節で代数方程式に対して導入した特異摂動法の
スケールの変更式(10.258)と
整合する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...のように求め10.15
- 実は3次の項を右辺に移項して
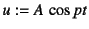 を代入した
逐次代入法[95]でも,同じ式を得ることができる。
を代入した
逐次代入法[95]でも,同じ式を得ることができる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...achenbach11.1
- 世界で最も高価なペーパーバックの教科書と言われていたことがある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,直応力11.2
- 棒を平面応力状態の1軸状態の物体と考えて,
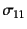 の
添え字を省略した。
の
添え字を省略した。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...である11.3
- 上の定式化では,
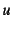 を
を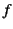 で,
で,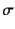 を
を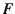 で表現したが,
以下
で表現したが,
以下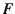 の代わりに
の代わりに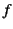 を用いている。
を用いている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
特殊な等号11.4
- 無限点で零になる十分滑らかな任意の関数
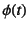 (試験関数
と呼ばれる)に対して
(試験関数
と呼ばれる)に対して
を満足するという意味の等号である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... argument)\fakejchar11.5
- すみませんが,理解できていません。Achenbach先生の授業の宿題でも
第1著者の答は間違っていた。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
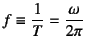 (単位は1/sあるいはHz)で定義される。
(単位は1/sあるいはHz)で定義される。