 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
この章は,元々は付録-Gの逆問題を定式化して, 非破壊評価をするための超音波探査法の講義のために北原先生が 起こしたものである。しかし北原先生も, この章の範囲と逆問題の定式化くらいまでしかカバーできていなかった。 それを引き継いだ第1著者のわかる範囲でまとめたのがこの章である。 地震応答問題等における平面波と表面波の初歩的な力学に限定されている。 なおここでは,アメリカ合州国Illinois州Evanston, Northwestern大学Achenbach教授の`Wave Propagation'の講義ノート(1980年頃)と 文献[1]11.1を 参考にした。
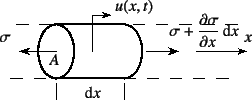
図-11.1に示したような,
一様断面の棒の中を軸方向に伝わる縦波の挙動を調べる。![]() 軸を
棒の長手方向にとり,断面積
軸を
棒の長手方向にとり,断面積![]() のある任意断面の
のある任意断面の![]() 方向の
変位を
方向の
変位を![]() ,直応力11.2を
,直応力11.2を![]() とすると,微分要素
とすると,微分要素![]() の
運動方程式は
の
運動方程式は
となる。ここで![]() は棒の単位長さ当りの質量である。また,
軸の伸びひずみ
は棒の単位長さ当りの質量である。また,
軸の伸びひずみ![]() は式(3.4)から
は式(3.4)から
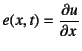 であり,
式(3.116a)の1次元のHookeの法則が成立して
であり,
式(3.116a)の1次元のHookeの法則が成立して
を満足する材料であるとする。さらに密度を![]() として
として![]() を
考慮すれば,上式の運動方程式は
を
考慮すれば,上式の運動方程式は
と定義した。鋼では![]() GN/m
GN/m![]() (kN/mm
(kN/mm![]() )と
)と![]() kg/m
kg/m![]() から
から![]() km/s程度になる。
km/s程度になる。
場所![]() と時間
と時間![]() の問題になっているので,上の運動方程式に唯一の解が
存在するためには,最低限,適切な初期条件と境界条件が必要になる。
初期条件は時刻
の問題になっているので,上の運動方程式に唯一の解が
存在するためには,最低限,適切な初期条件と境界条件が必要になる。
初期条件は時刻![]() に,任意の場所における
に,任意の場所における![]() と
と![]() を与えればいい。
これに対し境界条件は,棒の両端の
を与えればいい。
これに対し境界条件は,棒の両端の![]() そのものか
そのものか![]() ,
すなわち式(11.1)を考慮すると,
,
すなわち式(11.1)を考慮すると,![]() か
か![]() の
いずれかが適切な組み合わせで規定されていないといけない。
の
いずれかが適切な組み合わせで規定されていないといけない。
式(11.2)を解いてみよう。まず
という変数変換をし,
![]() と置き換えると,
偏微分の連鎖律から
と置き換えると,
偏微分の連鎖律から
という関係があるので,式(11.2)は
のような形の波動方程式であることがわかる。
この式(11.4)を2回積分すれば,例えば
となるので,元の関数形に戻すと
となる。2種類の解の重ね合わせになっていて,これをd'Alembertの解 と呼んでいる。
では
![]() という関数の物理的な意味を考察しよう。
例えばある時刻
という関数の物理的な意味を考察しよう。
例えばある時刻![]() にある場所
にある場所![]() で,この関数が
で,この関数が![]() という
値を持っていたとする。それから
という
値を持っていたとする。それから![]() 時間が
経った
時間が
経った
![]() のときの,
のときの,
![]() という場所の
この関数の値は
という場所の
この関数の値は
となる。つまり,![]() ,
, ![]() における「物理状態」が
における「物理状態」が![]() に
に![]() で
観察されたことになる。したがって,
で
観察されたことになる。したがって,
![]() という関数は
「
という関数は
「![]() の正の方向に
の正の方向に![]() で伝播する」物理現象を表している。
逆に
で伝播する」物理現象を表している。
逆に
![]() は
「
は
「![]() の負の方向に
の負の方向に![]() で伝播する」物理現象を表す。
で伝播する」物理現象を表す。
式(11.1)のHookeの法則を用いれば,応力![]() も
同様の関数形で求められて
も
同様の関数形で求められて
と表されることになる。ここで,プライムは
関数のargument(括弧の中の引数のこと;独立変数?)で
微分することを示しており
である。以下,この表現を用いるが,偏微分の連鎖律に十分気を付けること。
さて実際に問題を解く場合には,速度ではなく
と表現できる。この表現を用いると次のように扱うことができる。
と書くことができる。ここで
を用いていることに注意する。
つまり,応力![]() と速度
と速度![]() は同じargumentの関数で
表すことができることになり
は同じargumentの関数で
表すことができることになり
と置けばいい。
と置けばいい。
以下,簡単のために上に付したドットで時間微分を表し
速度を![]() と記すことにすると,上で求めた関係式から
と記すことにすると,上で求めた関係式から
(11.9)
という関係が成立する。 これは次の節で便利に使うことになる。
一例として,図-11.3のような長さ![]() の棒の
自由端を外力
の棒の
自由端を外力![]() でたたいたときの縦波の伝播を求めてみる。
初期条件は
でたたいたときの縦波の伝播を求めてみる。
初期条件は
である。
境界条件は,左端に作用しているのが圧縮力であることに注意して,
右端が固定されていることから
と与えられる。しかし,式(11.9)のように 速度と応力が同じ関数で表現できることから, 境界条件も応力と変位ではなく,速度も加えて表した方が便利だろう。 つまり
(11.10)
となるものとしよう。
まず最初の波が![]() に到達する前,つまり
に到達する前,つまり
![]() の間を検討しよう。
このときは,
の間を検討しよう。
このときは,![]() の正方向に進む波しか存在しないため,
任意点の応力の関数形は
の正方向に進む波しか存在しないため,
任意点の応力の関数形は
![]() である11.3はずだ。
しかし
である11.3はずだ。
しかし![]() における境界条件式(11.10a)から
における境界条件式(11.10a)から
を満足しなければならない。したがって,任意点の応力は
と求められる。
式(![]() )のように,
)のように,![]() と
と![]() の関数のargument同士が等しいという条件から,
この結論が得られていることを理解して欲しい。
端部をたたいたために,圧縮(負の応力)波が発生している。
そしてこれは進行波なので,式(11.9a)から速度が
の関数のargument同士が等しいという条件から,
この結論が得られていることを理解して欲しい。
端部をたたいたために,圧縮(負の応力)波が発生している。
そしてこれは進行波なので,式(11.9a)から速度が
となる。伝播する応力波を図-11.4に示した。
次に,最初の波が![]() に到達して反射したあと,
つまり
に到達して反射したあと,
つまり
![]() の間を検討しよう。
この状態は,進行波(入射する波なので入射波
と呼ぶ)と後退波(反射波
)が重ね合わさったものになる。つまり入射波は
の間を検討しよう。
この状態は,進行波(入射する波なので入射波
と呼ぶ)と後退波(反射波
)が重ね合わさったものになる。つまり入射波は
であり,応力の反射波が後退波なので
とすると
という表現になるはずである。添え字のIは入射波を,Rは反射波を指す。
これを重ね合わせた速度が![]() における
速度の境界条件式(11.10c)を満足しなければならないから
における
速度の境界条件式(11.10c)を満足しなければならないから
が成立する。右の式で
![]() と変数変換すると
と変数変換すると![]() は
は
という関数であることがわかる。
したがって,応力の反射波は
となるので,この二つの波を重ね合わせて
と表現できる。つまり第2項は,![]() の時間帯に,
の時間帯に,![]() を
始点として
を
始点として![]() の負方向に伝わる波を表している。図-11.5の
左図にその様子を示した。
の負方向に伝わる波を表している。図-11.5の
左図にその様子を示した。
さらに,最初の波先が反射して元の![]() まで戻ったあと,
つまり
まで戻ったあと,
つまり
![]() の間を検討しよう。
この場合は左端における反射波
の間を検討しよう。
この場合は左端における反射波
![]() が進行波として
さらに加わるので
が進行波として
さらに加わるので
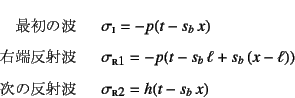
と置いていい。この重ね合わせた応力全体が,
境界条件式(11.10a)の![]() における条件
における条件
を満足しなければならないので,結局
と![]() が求められる。つまり
が求められる。つまり
が次の反射波になる。
ここでは応力の符号が変わって,引張りに転じたことに注意しなければならない。
したがって,以上の三つの波を重ね合わせた応力は
となる。![]() が短時間のみの作用の場合の例を図-11.5の
右図に示した。
が短時間のみの作用の場合の例を図-11.5の
右図に示した。
を与えたとき,
![]() の間の応力を求めよ。
ただし
の間の応力を求めよ。
ただし![]() とする。
もし,この棒の材料の引張り強度が
とする。
もし,この棒の材料の引張り強度が
![]() で
圧縮強度が
で
圧縮強度が![]() のとき,この棒はいつどこで最初に破断する可能性が高いか
示せ。文献[1]の問題から。
のとき,この棒はいつどこで最初に破断する可能性が高いか
示せ。文献[1]の問題から。
としてもいいHeaviside関数(階段関数)
で,図-10.16に示した。
この力による波が![]() の球に到達したあとの,応力の反射波と透過波を求めよ。
なお上式の
の球に到達したあとの,応力の反射波と透過波を求めよ。
なお上式の![]() は式(4.55)で定義したDiracの
デルタ関数で,いずれも正しくは関数ではなく超関数であるから,
最後の式の等号
は式(4.55)で定義したDiracの
デルタ関数で,いずれも正しくは関数ではなく超関数であるから,
最後の式の等号
![]() は
特殊な等号11.4である。文献[1]の問題から。
は
特殊な等号11.4である。文献[1]の問題から。