最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• 11.2.1 3次元の運動方程式
• 11.2.2 平面波
• 11.2.3 無限領域の調和平面波
  • 11.2.3.1 調和振動
  • 11.2.3.2 SH波の反射
    • 11.2.3.2.1 上半分が剛な場合:
    • 11.2.3.2.2 水平面が自由表面の場合:
  • 11.2.3.3 自由表面におけるP波の反射
  • 11.2.3.4 P波の反射と透過
  • 11.2.3.5 自由表面におけるSV波の反射

11.2 平面波

11.2.1 3次元の運動方程式

まず，3次元の連続体のつり合い式は式(3.22)であった。 したがって，連続体の運動方程式は，このつり合った 力の総和がNewtonの法則を満足する条件として得ることができる。 ここ以下では，p.で 規定した総和規約を用いて運動方程式を表現すると

$$\sigma_{ji,j}+X_i=\rho \ddot{u}_i$$ (11.12)

となり，これは式(3.96)と同じである。 添え字にあるコンマは，その次の添え字に相当する独立変数で微分することを 意味する。 ここに$\fat{X}$は体積力であるが，つり合っている弾性体への 付加的な作用によって波が生じる場合を対象とするので，以下では無視する。 またHookeの法則は式(3.42)に示したように

$$\sigma_{ij}= 2\mu \epsilon_{ij} + \lambda \delta_{ij} \epsilon_{kk}$$ (11.13)

と書くことができる。 ここに $\fat{\epsilon}$はひずみテンソルであり，$\mu$と$\lambda$はLaméの 定数である。また$\delta_{ij}$はKroneckerのデルタである。 さらにひずみは式(3.6)で定義したように，変位と

$$\epsilon_{ij}= \dfrac12 \left(u_{i,j}+u_{j,i}\right)$$ (11.14)

のように関係付けられている。式(11.14)を式(11.13)に 代入したあと，それを式(11.12)に代入して整理すると， 変位で表した運動方程式は

$$\left(\lambda+\mu\right) u_{j,ji}+\mu u_{i,jj}=\rho \ddot{u}_i$$ (11.15)

となる。あるいは

$$\left(\lambda+\mu\right) (u_{j,j})_{,i}+\mu u_{i,jj}=\rho\... ...la}\cdot \fat{u}) +\mu \nabla^2 \fat{u}=\rho \ddot{\fat{u}}$$

のような表現も可能である。 各自がわかり易い方を使うといい。節-3.5.1では2種類の ポテンシャルを用いて波動方程式を誘導したが，ここでは， もう少し物理的なアプローチを用いて最も基本的な波である 平面的に伝わる波の波動方程式を誘導し，それを解くことにしよう。

11.2.2 平面波

図 11.7: 平面状の波

ある観測地から非常に遠い活断層で地震が発生したとすると， その震源は観測地から見たとき，ほとんど点源にしか見えないだろう。 その点源からは球面状の波動が発生するのではあるが， 観測地が震源からとても遠いため，そこに到達する波は点源からの 曲率半径がとても大きな球面波であり，それは ほぼ平面状の現象が伝播する波として近似しても， 工学的には問題は生じないであろう。さて， 式(11.5)で示したように，1次元の進行波は$f(x-c_b t)$という 関数形で表現できる。この関数は， $x=\mbox{const.}$の面の物理現象が， その面の法線方向つまり$x$方向に$c_b$の速さで伝播していることを 示している。 一方3次元空間の任意の平面は，図-11.7に 示したように $p_1 x_1+p_2 x_2+p_3 x_3=\mbox{const.}$で定義できる。 つまり，$\fat{p}$をある平面の単位法線ベクトルとすると， その平面は $\fat{x}\cdot\fat{p}=x_k p_k=\mbox{const.}$と表すことができる。 したがって，1次元の進行波からの類推で，3次元空間の平面波の場合は

$$\fat{u}=\fat{d} f(\fat{x}\cdot\fat{p}-c t)\quad\mbox{あるいは}\quad u_i=d_i f(x_k p_k-c t)$$ (11.16)

という関数で，変位を表現できることは容易に推測できるだろう。 ここに，$\fat{d}$は変位ベクトルの向きを表す単位ベクトルであり，$c$は 考えている波の位相速度である。 $\left(\fat{x}\cdot\fat{p}-c t\right)$を 位相と呼ぶこともある。

式(11.16)のような平面状の波が存在するかどうかを 調べるために，それを式(11.15)の運動方程式に代入してみよう。 そのために式(11.16)を微分すると

$$u_{i,j}=d_i p_j f'(x_k p_k-ct), \quad u_{i,jj}=d_i p_j p... ...ad u_{j,ji}=d_j p_j p_i f'', \quad \ddot{u}_i=c^2 d_i f''$$

等という関係が成り立つ。第2式では$\fat{p}$が単位ベクトルで あること$(p_j p_j=1)$を用いた。これを運動方程式に代入して整理すると

$$\left\{ \left(\lambda+\mu\right) \left(d_j p_j\right) p_i+ \mu d_i-\rho c^2 d_i\right\} f''(x_k p_k-ct)=0$$

となるので，この関数形を持った解が存在するためには，係数が零で なければならないから

$$\left(\mu-\rho c^2\right) d_i+ \left(\lambda+\mu\right) \left(d_j p_j\right) p_i=0$$ (11.17)

が成立していなければならない。

この式(11.17)が成り立つ可能性は二つある。

1. 一つは $\fat{p}=\pm\fat{d}$つまり$p_i=\pm d_i$の場合である。 これは，平面状の運動は平面の法線方向であることを示している。 これを上式(11.17)に代入すると
   
   $$\left\{\left(\mu-\rho c^2\right)+\left(\lambda+\mu\right)\ri... ...} d_i=0 \quad\to\quad \left(\lambda+2\mu\right)-\rho c^2=0$$
   
   

   となる。つまり，位相速度が式(3.100a)で定義したものと同じく
   

   $$c=c\subsc{l}\equiv\sqrt{\dfrac{\lambda+2\mu}{\rho}}$$ (11.18)

   
   

   で定義される縦波（P波） の速度になる。この場合は
   

   $$\fat{\nabla}\times\fat{u}= \fat{d}\times\fat{p} f'(\fat{x}... ...f'=0 \quad \left[\because \fat{d}\times\fat{d}=\fat{0}\right]$$
   
   

   を満たす運動，つまり非回転波 になっている。 これはせん断変形が伝播するのではなく，1次元の波動のような疎密波に相当する。

2. もう一つの可能性は $\fat{p}\cdot\fat{d}=0$つまり$p_i d_i=0$の 場合である。つまり，平面状の運動が平面の法線方向と直角方向になっている。 これを上式(11.17)に代入すると
   

   $$\mu-\rho c^2=0 \quad\to\quad c=c\subsc{t}\equiv\sqrt{\dfrac{\mu}{\rho}}<c\subsc{l}$$ (11.19)

   
   

   となるから，位相速度は式(3.100b)で定義された横波（S波） の速度になる。この場合は
   

   $$\fat{\nabla}\cdot\fat{u}= \fat{d}\cdot\fat{p} f'(\fat{x}\c... ...bsc{t} t)=0 \quad\left[\because \fat{d}\cdot\fat{p}=0\right]$$
   
   

   を満たす運動，つまり等体積波 になっている。 これは体積変形が無いまません断変形が伝播していることになる。

以下では，$x_1$-$x_3$平面が水平面と平行で， 波の進行方向$\fat{p}$が$x_1$-$x_2$平面内にある場合を対象とする。 その条件下で，図-11.8に示したような， 次の3種類の波の挙動を検討する。

P波:

縦波で，変位ベクトルの向き$\fat{d}$が$x_1$-$x_2$平面内に あるものとする。

SH波:

横波のうち，$\fat{d}$が$x_3$方向にある波， つまり $\fat{d}=\lfloor 0 0 1\rfloor\supersc{t}$である。 したがって平面状の運動は$x_1$-$x_2$平面の法線方向に生じ， 水平（$x_3$）方向の運動になっているため，H[orizontal]の 文字を用いている。面外波 と呼ぶこともある。

図 11.8: P波・SH波・SV波

SV波:

横波のうち，$\fat{d}$も$x_1$-$x_2$平面内にある波である。 平面状の運動は$x_1$-$x_2$平面内に生じ， 水平方向ではない（傾いた鉛直方向の）運動になっているため，V[ertical]の 文字を用いている。面内波 と呼ぶこともある。

11.2.3 無限領域の調和平面波

11.2.3.1 調和振動

これまでは$f(\cdot)$の関数形は任意として扱い， 初期条件や境界条件で決まるものだったが， ここからは定常運動を対象として，定周期運動とする。 つまり振幅$A$の調和振動運動として

$$f(\fat{x}\cdot\fat{p}-c t)=A \exp\left(\mbox{i}\eta\right)... ...-c t\right)= k \left(\fat{x}\cdot\fat{p}\right)-\omega t$$ (11.20)

とする。ここに $k\equiv\slfrac{\omega}{c}$は 波数であり，$\omega$は振動数である。 また，波が伝播する領域は図-11.9のように， 水平面$x_2=0$で上下に別々の領域に分割されているものを対象とする。

11.2.3.2 SH波の反射

図 11.9: SH波の反射

SH波は，図-11.9に示した $\fat{d}=\lfloor 0 0 1\rfloor\supersc{t}$の波である。 後述のような境界条件の検討から明らかになることではあるが， このSH波の反射ではSH波しか生じない。したがって， 入射する波も反射波も，生じる変位は$x_3$方向成分$u_3$のみである。 そこで図のように角度と波の進むベクトルを定義すると

$$\fat{p}^{(0)}=\left\{\begin{array}{c} \sin\theta_0 \cos\... ...array}{c} \sin\theta_2 -\cos\theta_2 \end{array}\right\}$$ (11.21)

となるので，入射波は

$$u_3^{(0)}=A_0 \exp\left\{\mbox{i} k_0 \left( x_1 \sin\theta_0+x_2 \cos\theta_0-c\subsc{t} t \right) \right\}$$ (11.22)

であり，反射波は

$$u_3^{(2)}=A_2 \exp\left\{\mbox{i} k_2 \left( x_1 \sin\theta_2-x_2 \cos\theta_2-c\subsc{t} t \right) \right\}$$ (11.23)

となる。$A_0$, $A_2$は複素数の振幅である。

11.2.3.2.1 上半分が剛な場合:

例えば比較的硬いものの下で生じる反射を モデル化したものとして，$x_2=0$より上が剛な場合をまず考えよう。 この場合，$x_2=0$の境界条件は$u_3=0$であるから，入射波と反射波の 重ね合わせから

$$u_3(x_2=0) = u_3^{(0)}(x_2=0)+u_3^{(2)}(x_2=0)$$

$$= A_0 \exp\left\{\mbox{i} k_0 \left(x_1 \sin\theta_0-c\subsc{t... ...p\left\{\mbox{i} k_2 \left(x_1 \sin\theta_2-c\subsc{t} t \right)\right\}=0$$ (11.24)

が任意の$x_1$, $t$で成立しなければならない。 つまり，二つの指数関数($\exp$)の形は共に同じでなければならず，$x_1$の 係数同士と$t$の係数同士から

$$k_0 \sin\theta_0=k_2 \sin\theta_2, \quad k_0=k_2$$

が成り立つ必要がある。よって

$$k_2=k_0, \qquad \theta_2=\theta_0$$ (11.25)

となるから，境界条件式(11.24)に代入し直せば

$$A_2=-A_0$$ (11.26)

と求められる。したがって，定常状態にある波の$x_3$方向変位は， この結果を反射波の式(11.23)に代入したものと 入射波の式(11.22)とを重ね合わせて

$$u_3(x_1,x_2,t) = A_0 \exp\left\{\mbox{i} k_0 \left(x_1 \sin\theta_0+x_2 \cos... ...} k_0 \left(x_1 \sin\theta_0-x_2 \cos\theta_0-c\subsc{t} t\right)\right\}$$

$$= 2\mbox{i} A_0 \sin\left(k_0 x_2 \cos\theta_0\right) \exp\left\{ \mbox{i} k_0 \left( x_1 \sin\theta_0-c\subsc{t} t\right)\right\}$$ (11.27)

となる。解の最初の関数 $\sin\left(k_0 x_2 \cos\theta_0\right)$の 部分は，深さ方向の$x_2$方向にはsine関数状の振幅分布をすることを 示しており，このような波を重複波 と呼んでいる。また二つ目の指数関数は， その引数が $(x_1 \sin\theta_0-c\subsc{t} t)$であることから，$x_1$の正の 方向に速さ $\dfrac{c\subsc{t}}{\sin\theta_0}$で進む進行波 であることを示している。

11.2.3.2.2 水平面が自由表面の場合:

次に，例えば水平面より上が大気（真空）であるような 場合の反射をモデル化したものとして，$x_2=0$が自由表面である場合を考えよう。 このときの$x_2=0$の 境界条件は$\sigma_{i2}=0$ ($i=1$, 2, 3)である。SH波は$u_1=0$, $u_2=0$, $u_3=u_3(x_1, x_2)$なので，各ひずみ成分は $\epsilon_{11}=0$, $\epsilon_{22}=0$, $\epsilon_{33}=0$, $\epsilon_{12}=0$となるので，Hookeの 法則から$\sigma_{12}=0$と$\sigma_{22}=0$は常に成立する。 したがって残った条件は

$$\sigma_{32}=2\mu \epsilon_{32}=\mu u_{3,2}=0$$

となる。このことから自由表面の境界条件は

$$u_{3,2}=0$$ (11.28)

で与えられる。剛体の場合と同様に，入射波と反射波の重ね合わせで 境界条件式(11.28)を表すと

$$u_{3,2}(x_2=0) = u_{3,2}^{(0)}(x_2=0)+u_{3,2}^{(2)}(x_2=0)$$ (11.29)

$$= \mbox{i} k_0 A_0 \cos\theta_0 \exp\left\{\mbox{i} k_0 \lef... ...p\left\{\mbox{i} k_2 \left(x_1 \sin\theta_2-c\subsc{t} t \right)\right\}=0$$

が，任意の$x_2$, $t$で成り立たなければならない。したがって

$$k_2=k_0,\quad \theta_2=\theta_0 \quad A_2=A_0$$ (11.30)

が解になる。よって，定常状態の変位は，剛体の場合とほぼ同様に

$$u_3(x_1,x_2,t) = 2 A_0 \cos\left(k_0 x_2 \cos\theta_0\ri... ...k_0 \left( x_1 \sin\theta_0-c\subsc{t} t\right)\right\}$$ (11.31)

と求められる。境界条件の違いは，重複波の部分のみに現れている。

11.2.3.3 自由表面におけるP波の反射

SH波は，境界条件によらずSH波の反射しか生じなかったが，P波の場合には， 例えば

P, SV波が発生:

次の条件のとき

1. 上領域が剛なとき: $u_1=0$, $u_2=0$
2. 自由表面のとき: $\sigma_{21}=0$, $\sigma_{22}=0$

P波のみが発生:

次の条件のとき

1. $u_1=0$, $\sigma_{22}=0$
2. 摩擦の無い境界のとき: $u_2=0$, $\sigma_{21}=0$

のような反射が生じることがわかっている。

図 11.10: P波の反射

ここでは代表的な例として， 自由表面が存在する場合の半無限体を対象として解くので， その他の場合については各自試してみて欲しい。図-11.10に 示したように角度とベクトルを定義すると， 三つの波の変位を$n=0$, 1, 2で区別して

$$u_i^{(n)} = A_n d_i^{(n)} \exp\left(\mbox{i} \eta_n\right) \quad (i=1, 2),$$ (11.32)

$$\eta_n\equiv k_n \left(x_1 p_1^{(n)}+x_2 p_2^{(n)}-c_n t\right)$$

と表すことができる。ここに

$$\mbox{入射P波:} \quad \fat{d}^{(0)}=\fat{p}^{(0)}=\left\{ \begin{... ...}{c} \sin\theta_1 -\cos\theta_1 \end{array} \right\}, \quad c_1=c\subsc{l},$$

$$\mbox{}\qquad\qquad\qquad \mbox{反射SV波:} \quad \fat{d}^{(2)}=\l... ...y}{c} \sin\theta_2 -\cos\theta_2 \end{array} \right\}, \quad c_2=c\subsc{t}$$ (11.33)

である。ひずみ成分はそれぞれ

$$\epsilon_{11}^{(n)} = u_{1,1}^{(n)}=\mbox{i} k_n p_1^{(n)} d_1^{(n)} A_n \exp\lef... ...=\mbox{i} k_n p_2^{(n)} d_2^{(n)} A_n \exp\left(\mbox{i} \eta_n \right),$$

$$2\epsilon_{12}^{(n)} = u_{1,2}^{(n)}+u_{2,1}^{(n)}=\mbox{i} k_n \left( d_1^{(n)} p_2^{(n)}+d_2^{(n)} p_1^{(n)} \right) A_n \exp\left(\mbox{i} \eta_n \right)$$ (11.34)

と書くことができるので，Hookeの法則に代入して，各応力成分も

$$\sigma_{22}^{(n)} = \left(\lambda+2\mu\right) \epsilon_{22}^{(n)} +\lambda \epsilon... ...+\lambda d_1^{(n)} p_1^{(n)} \right\} A_n \exp\left(\mbox{i} \eta_n\right)$$

$$\sigma_{12}^{(n)} = 2\mu \epsilon_{12}^{(n)}= \mbox{i} k_n \mu \left\{d_2^{(n)} p_1^{(n)}+d_1^{(n)} p_2^{(n)} \right\} A_n \exp\left(\mbox{i} \eta_n\right)$$ (11.35)

となる。

自由表面の境界条件は$x_2=0$で$\sigma_{22}=0$, $\sigma_{21}=0$なので， 式(11.35)の重ね合わせから

$$\sigma_{22}(x_2=0) = \sum_{n=0}^2 \sigma_{22}^{(n)}(x_2=0) = \sum_{n=0}^2 \mbox{i} k_... ...^{(n)} p_1^{(n)} \right\} A_n \exp\left(\mbox{i} \overline{\eta}_n\right)=0$$

$$\sigma_{21}(x_2=0) = \sum_{n=0}^2 \sigma_{21}^{(n)}(x_2=0)= \sum_{n=0}^2 \mbox{i} k_n... ...^{(n)} p_2^{(n)} \right\} A_n \exp\left(\mbox{i} \overline{\eta}_n\right)=0$$ (11.36)

となる。ここに $\overline{\eta}_n\equiv \eta_n(x_2=0)= k_n \left(x_1 p_1^{(n)}-c_n t\right)$と置いた。 この条件式に式(11.33)を代入して整理すると

$$\mbox{i} k_0 \left(\lambda+2\mu \cos^2\theta_0\right) A_0 \... ...2\mu \cos^2\theta_1\right) A_1 \exp\left(\mbox{i} \overline{\eta}_1\right)$$

$$\mbox{}\qquad\qquad\qquad\qquad\qquad\qquad\qquad -2 \mbox{i} k_... ...sin\theta_2 \cos\theta_2 A_2 \exp\left(\mbox{i} \overline{\eta}_2\right)=0$$

$$2\mbox{i} k_0 \mu \sin\theta_0 \cos\theta_0 A_0 \exp\left(... ...,\sin\theta_1 \cos\theta_1 A_1 \exp\left(\mbox{i} \overline{\eta}_1\right)$$

$$\mbox{}\qquad\qquad\qquad\qquad\qquad\qquad\qquad +\mbox{i} k_2\... ...eta_2-\cos^2\theta_2\right) A_2 \exp\left(\mbox{i} \overline{\eta}_2\right)=0$$ (11.37)

となる。この式が任意の$x_1$, $t$で成立するためには，まず指数関数同士が 等価でなければならないから

$$k_0 c\subsc{l}=k_1 c\subsc{l}=k_2 c\subsc{t}=\omega, \qua... ...a_0=k_1 \sin\theta_1=k_2 \sin\theta_2= \mbox{見かけの波数}$$ (11.38)

の条件が成り立つ必要がある。後者はSnellの法則 と呼ばれる。したがって

$$k_1=k_0,\quad k_2=\kappa k_0, \quad \kappa\equiv \dfrac{c\... ...\dfrac{\lambda+2\mu}{\mu}}=\sqrt{\dfrac{2(1+\nu)}{1-2\nu}}>1$$ (11.39)

となり，角度は

$$\theta_1=\theta_0, \quad \sin\theta_2=\dfrac{k_0}{k_2} \si... ...} \sin\theta_0 < 1 \quad\to\quad \theta_2<\theta_1=\theta_0$$ (11.40)

と求められる。$\kappa$が1より大きいことから，$\theta_2$が必ず 実数として存在し，最後の式で示したように，その値は$\theta_1$より 小さいことには注意する。この結果を式(11.37)に代入して整理すると

$$\left(\lambda+2\mu \cos^2\theta_0\right) \dfrac{A_1}{A_0}... ...a \cos 2\theta_2 \dfrac{A_2}{A_0}=\sin 2\theta_0 \eqno{(*)}$$

となる。第1式を$\mu$で除して $\kappa^2=\slfrac{\lambda}{\mu}+2$を使うと

$$\left(\kappa^2-2 \sin^2\theta_0\right) \dfrac{A_1}{A_0} -... ...2 \dfrac{A_2}{A_0}= -\left(\kappa^2-2 \sin^2\theta_0\right)$$

と書き換えられ，さらに $\sin\theta_0=\kappa \sin\theta_2$を 使えば， $\kappa^2-2 \sin^2\theta_0=\kappa^2 \cos 2\theta_2$となるので， この式は

$$\kappa \cos 2\theta_2 \dfrac{A_1}{A_0}- \sin 2\theta_2 \dfrac{A_2}{A_0}=-\kappa \cos 2\theta_2$$

となり，結局上の二つの式($\ast$)は

$$\left(\begin{array}{cc} \kappa \cos 2\theta_2 & -\sin 2\th... ... -\kappa \cos 2\theta_2 \sin 2\theta_0 \end{array}\right\}$$

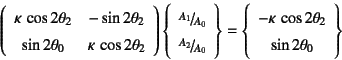
と書き換えられる。したがって

$$\left\{\begin{array}{c} \slfrac{A_1}{A_0} \slfrac{A_2}{A_... ...quiv \sin 2\theta_0 \sin 2\theta_2+\kappa^2 \cos^2 2\theta_2$$

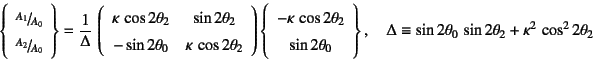
となることから

$$\dfrac{A_1}{A_0}= \dfrac{\sin 2\theta_0 \sin 2\theta_2-\kap... ... {\sin 2\theta_0 \sin 2\theta_2+\kappa^2 \cos^2 2\theta_2}$$ (11.41)

と求められる。これから

1. $\theta_0=0$の場合には， $\theta_1=\theta_2=0$, $A_2=0$に なるため，反射はP波のみになり，$A_1=-A_0$になる。 ただし， $A_0 d_2^{(0)}=A_1 d_2^{(1)}$になることから，$u_2$の 入射波と反射波が同位相になっているため，重複波になる。
2. $\theta_0=\slfrac{\pi}{2}$の 場合（かすめ入射 と呼ばれる）にも$A_2=0$になり，反射はP波のみである。 ただし，この場合は $A_0 d_1^{(0)}=-A_1 d_1^{(1)}$になることから，$u_1$の 入射波と反射波は逆位相になるため，$u_1=0$になる。 真横からの入射なのに波動が伝わらないというのは一体?
3. $\sin 2\theta_0 \sin 2\theta_2=\kappa^2 \cos^2 2\theta_2$を 満たすような$\theta_0$で入射した場合には$A_1=0$になるから， 反射はSV波のみになる。 このような現象をモード変換 と呼ぶ。

といった特徴が明らかになる。

11.2.3.4 P波の反射と透過

図 11.11: P波の反射と透過

次に，上半分の領域の材料が下半分のそれとは異なる場合の無限領域における， その二つの領域境界を通した反射と透過について， その概要を説明しておく。図-11.11に 示したように角度とベクトルを定義すると， 上半分の領域の透過波についても$n=3$, 4で区別すれば，その変位を 同じ式(11.32)で表すことができる。 また透過波についての諸量は

$$\mbox{透過P波:} \quad \fat{d}^{(3)}=\fat{p}^{(3)}=\left\{ \begin{array}{c} \sin\theta_3... ...}\supersc{b}\equiv \sqrt{\dfrac{\lambda\subsc{b}+2\mu\subsc{b}}{\rho\subsc{b}}}$$

$$\mbox{透過SV波:} \quad \fat{d}^{(4)}=\left\{ \begin{array}{c} -\cos\theta_4 \sin\the... ...)}=\left\{ \begin{array}{c} \sin\theta_4 \cos\theta_4 \end{array} \right\},$$

$$\mbox{}\qquad\qquad c_4=c\subsc{t}\supersc{b}\equiv \sqrt{\dfrac{\mu\subsc{b}}{\rho\subsc{b}}}$$ (11.42)

である。ここに，$\mu\subsc{b}$, $\lambda\subsc{b}$が 上半分の領域のLaméの定数であり，$\rho\subsc{b}$が密度である。 これによる応力成分も前節同様に表現でき

$$\sigma_{22}^{(n)}= \mbox{i} k_n \left\{\left(\lambda\subs... ... p_2^{(n)} \right\} A_n \exp\left(\mbox{i} \eta_n\right)$$ (11.43)

となる。

この$x_2=0$における条件は，二つの変位成分と，応力の 二つの成分$\sigma_{22}$, $\sigma_{21}$が， それぞれ連続していることになるので 式(11.35) (11.43)の重ね合わせから

$$\sum_{n=0}^2 A_n d_i^{(n)} \exp\left(\mbox{i} \overline{\eta}_... ...ght)= \sum_{n=3}^4 A_n d_i^{(n)} \exp\left(\mbox{i} \overline{\eta}_n\right)$$

$$\sum_{n=0}^2 \mbox{i} k_n \left\{\left(\lambda+2\mu\right) d_2... ..._1^{(n)} p_1^{(n)} \right\} A_n \exp\left(\mbox{i} \overline{\eta}_n\right)$$

$$\sum_{n=0}^2 \mbox{i} k_n \mu \left\{d_2^{(n)} p_1^{(n)}+d_1^... ..._1^{(n)} p_2^{(n)} \right\} A_n \exp\left(\mbox{i} \overline{\eta}_n\right)$$ (11.44)

となる。ここでも前節同様， $\overline{\eta}_n\equiv \eta_n(x_2=0)= k_n \left(x_1 p_1^{(n)}-c_n t\right)$と置いてある。 この条件式に式(11.33) (11.42)を代入して整理すれば 角度や振幅の間の関係式を得る。 まず指数関数同士が等価でなければならないから

$$k_1=k_0,\quad k_2=\kappa k_0, \quad k_3=\alpha\subsc{b} k_0, \quad k_4=\beta\subsc{b} k_0$$ (11.45)

となる。ここに

$$\alpha\subsc{b}\equiv \dfrac{c\subsc{l}}{c\supersc{b}\subsc... ... \dfrac{c\subsc{l}}{c\supersc{b}\subsc{t}} >\alpha\subsc{b}$$ (11.46)

であり，$\kappa$は式(11.39)で定義した。 また角度は

$$\theta_1=\theta_0, \quad \sin\theta_2=\dfrac{1}{\kappa} \s... ...eta_4=\dfrac{1}{\beta\subsc{b}} \sin\theta_0 <\sin\theta_3$$ (11.47)

と求められる。これを上式(11.44)に代入し直せば， 各振幅比を求めることができる。 以下面倒なので結果は省略する。

11.2.3.5 自由表面におけるSV波の反射

図-11.10に示した左からの入射波がSV波である場合を 考えよう。この場合には

$$\mbox{入射SV波:} \quad \fat{d}^{(0)}=\left\{ \begin{array}... ... \cos\theta_0 \end{array} \right\}, \quad c_0=c\subsc{t}$$ (11.48)

となる以外は，式(11.33)と同じになっている。 これを用いて自由表面の境界条件に代入すると

$$2\mbox{i} k_0 \mu \sin\theta_0 \cos\theta_0 A_0 \exp\left(... ...2\mu \cos^2\theta_1\right) A_1 \exp\left(\mbox{i} \overline{\eta}_1\right)$$

$$\mbox{}\qquad\qquad\qquad\qquad\qquad\qquad\qquad -2 \mbox{i} k_... ...sin\theta_2 \cos\theta_2 A_2 \exp\left(\mbox{i} \overline{\eta}_2\right)=0$$ (11.49)

$$\mbox{i} k_0 \mu \left(\sin^2\theta_0-\cos^2\theta_0\right) A... ...,\sin\theta_1 \cos\theta_1 A_1 \exp\left(\mbox{i} \overline{\eta}_1\right)$$

$$\mbox{}\qquad\qquad\qquad\qquad\qquad\qquad\qquad +\mbox{i} k_2\... ...a_2-\cos^2\theta_2\right) A_2 \exp\left(\mbox{i} \overline{\eta}_2\right)=0$$

となる。したがって，指数関数の形から

$$k_0 c\subsc{t}=k_1 c\subsc{l}=k_2 c\subsc{t}, \quad k_0 \sin\theta_0= k_1 \sin\theta_1= k_2 \sin\theta_2$$ (11.50)

でなければならないため

(11.51)

と求められる。この結果を式(11.49)に代入して整理すると

$$\left(\lambda+2\mu \cos^2\theta_1\right) \dfrac{A_1}{A_0}... ... \cos 2\theta_0 \dfrac{A_2}{A_0}=\kappa \mu \cos 2\theta_0$$

となる。これを解けば

$$\dfrac{A_1}{A_0}=\dfrac{-\kappa \sin 4\theta_0}% {\sin 2\t... ... {\sin 2\theta_0 \sin 2\theta_1+\kappa^2 \cos^2 2\theta_0}$$ (11.52)

と求められる。この結果からは

1. $\theta_0=0, \slfrac{\pi}{4}, \slfrac{\pi}{2}$の 場合には，$A_1=0$になり，反射はSV波のみになる。
2. $\sin 2\theta_0 \sin 2\theta_1=\kappa^2 \cos^2 2\theta_0$を 満たすような$\theta_0$で入射した場合には$A_2=0$になるから， 反射はP波のみになる。これもモード変換である。

といった特徴が明らかになる。

ところが，式(11.39)で 示したように$\kappa>1$であることから，式(11.51d)からは

$$\theta_0<\theta\sub{cr}\equiv \sin^{-1}\left(\dfrac{1}{\kappa}\right)$$ (11.53)

の条件を満足するように入射しない限り，$\theta_1$が 実数にはならないことがわかる。では， $\theta_0>\theta\sub{cr}$のときには どのような現象になっているのか考察してみよう。この場合には

$$\cos^2\theta_1=1-\sin^2\theta_1=1-\kappa^2 \sin^2\theta_0<0... ...\quad \beta\equiv \sqrt{\sin^2\theta_0-\dfrac{1}{\kappa^2}}$$ (11.54)

と置こう。これより

$$p_1^{(1)}=\sin\theta_1=\kappa \sin\theta_0, \quad p_2^{(1)}=-\cos\theta_1=-\mbox{i} \kappa \beta$$

となるので，反射P波の変位成分は

$$u_i^{(1)}=A_1 d_i^{(1)} \exp\left\{ \mbox{i} k_1 \left... ...1-\dfrac{c\subsc{l}}{\kappa \sin\theta_0} t\right)\right\}$$ (11.55)

となる。この波は，$x_1$の正方向には 速さ $\dfrac{c\subsc{l}}{\kappa \sin\theta_0}$で進む波になってはいるが， 深さ方向の$x_2<0$の領域では， $\exp\left(k_0 \beta x_2\right)$のように 指数関数的に振幅が小さくなる波になっている。 すなわち，浅い部分においてのみ顕著な振幅を持つ波になっている。 表面のみで顕著な波なので，表面波と呼ばれている。これについては 次節で検討しよう。

1. $x_2=0$を挟んだ上半分のせん断弾性係数が$\mu\subsc{b}$で， 下半分のそれが$\mu$であるような，図-11.11に示した 無限領域を対象とする。 この領域に，左下からSH波が$\theta_0$で入力($n=0$)した場合の， 反射SH波($n=2$)と透過SH波($n=4$)の特性を求めよ。

   特に，透過する波の振幅の 増幅率 $\dfrac{A_4}{A_0}$と角度$\theta_4$を用いて， 地震波の増幅の仕方と角度の変化について議論したい。 文献[85]には右表に示したような地盤の基盤の加速度記録と 表層の加速度記録が示されており，その加速度振幅の増幅率は2.8倍になっている。 これを，最初に表面に到達するSH波の増幅率を用いて計算してみよ。 なお，簡単のために最初以外の反射波は無視していい。 入射角度は$\theta_0=0$と60度の場合について求めてみよ。

   
   

   層	$\rho$ (kg/m$^3$)	$\mu$ (MN/m$^2$)
   表層	1500	12
   第2層	1670	28
   第1層	1850	56
   基盤	1950	490

   
   

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。