 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
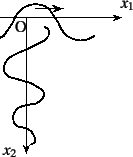
図-11.12のように,![]() 方向に進む波であるが,
その振幅が
方向に進む波であるが,
その振幅が![]() 方向に向かって指数関数的に小さくなるような波が
存在できるかどうかについて考えてみよう。
ここでは
方向に向かって指数関数的に小さくなるような波が
存在できるかどうかについて考えてみよう。
ここでは![]() は下向きを正にしてあり,
は下向きを正にしてあり,![]() の水平面は自由表面とする。
この運動に対応した変位成分
の水平面は自由表面とする。
この運動に対応した変位成分
の存在の可能性を検討しようとしている。
ただし,深くなるほど振幅は小さくなるものと考えるため,少なくとも
境界条件は![]() で
で![]() ,
, ![]() であるから,
ひずみの定義とHookeの法則を用いれば
であるから,
ひずみの定義とHookeの法則を用いれば
になる。また運動方程式は式(11.15)から
である。式(11.56)を式(11.59)に
代入して
![]() の
係数同士を比べると
の
係数同士を比べると
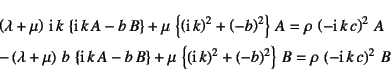
が成立しなければならない。したがって
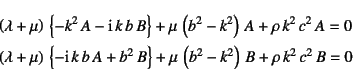
つまり
でなければならない。右辺が零なので,解が存在するためには,
この式の係数行列が特異でなければならない。つまり
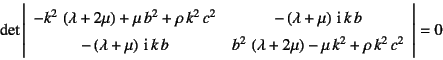
に![]() と
と![]() の定義を用いれば
の定義を用いれば
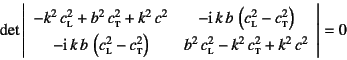
であればいいことになる。これを整理すると
を満足するような![]() と
と![]() ,
, ![]() が存在すれば,表面波の存在が可能になる。
この式から,まず
が存在すれば,表面波の存在が可能になる。
この式から,まず
という関係が成立する。
![]() であり,
式(11.57)のように
であり,
式(11.57)のように![]() でなければならないことから,
この式(11.62)の形は
でなければならないことから,
この式(11.62)の形は
であることを示唆している。
式(11.60)も![]() ,
, ![]() を用いて書き直すと
を用いて書き直すと
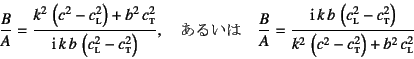
とも書き表すことができるので,これに式(11.62)を代入すると
と求められる。この関係を用いると,変位成分は
と求められる。
あとは波の速さ![]() を決定すればいいわけだが,その方程式は境界条件から
求めることができる。つまり,式(11.63)を
境界条件式(11.58)に代入すれば
を決定すればいいわけだが,その方程式は境界条件から
求めることができる。つまり,式(11.63)を
境界条件式(11.58)に代入すれば
となり,![]() ,
, ![]() を用いると
を用いると
と書き換えられる。これを整理すると
と書き表すことができる。つまり
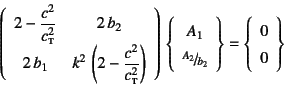
が![]() ,
, ![]() として意味のある解を与えれば,表面波が存在できることになる。
したがって,この上式の係数行列が特異になる条件から
として意味のある解を与えれば,表面波が存在できることになる。
したがって,この上式の係数行列が特異になる条件から
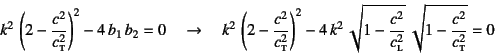
つまり
が成立しなければならない。この式の解![]() がRayleigh波の
速さ
がRayleigh波の
速さ![]() である。ここで
である。ここで
![]() に対して
に対して
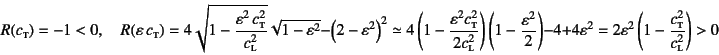
であることから,
![]() に少なくとも一つの
実数解
に少なくとも一つの
実数解![]() を持つことが期待できる。
さらに複素関数論における「偏角の原理
11.5」から,
を持つことが期待できる。
さらに複素関数論における「偏角の原理
11.5」から,![]() は2個の実数解しか
持たないことが証明でき,
は2個の実数解しか
持たないことが証明でき,![]() が
が![]() の
関数であることから,その2個は符号のみが異なる二つの解であることがわかる。
したがって,Rayleigh波の速さは
の
関数であることから,その2個は符号のみが異なる二つの解であることがわかる。
したがって,Rayleigh波の速さは
を満たすものとして唯一に決定できる。 このような表面波は,地震が終わったあとに地球を一周して到達することがあると されている。
前節のRayleigh波はSV波的な表面波であったが,
では,表面SH波は存在するだろうか。式(11.56)と
同様の面外変位を
と設定して確かめてみよう。運動方程式で意味のあるのは![]() 方向の
方向の
のみであるから,これに上式を代入して
![]() を
考慮すると,
を
考慮すると,
![]() の係数同士の
等価性から
の係数同士の
等価性から
と求められる。また,境界条件は![]() で
で![]() つまり
つまり![]() で
あるから
で
あるから
となり,![]() であるためには
であるためには
しかあり得ないことになる。つまり,面外波の表面波は存在しないことになる。
しかし,もし図-11.13のように表面近くに
材料特性が異なる層が存在した場合には,面外の表面波が存在し得ることが
わかっている。
そのような波をLove波と呼ぶ。そこで,変位を
と仮定する。ここに![]() と
と![]() は式(11.67)を満足しているものとする。
境界条件は
は式(11.67)を満足しているものとする。
境界条件は
であり,![]() における
における![]() と
と![]() の
連続条件は,
の
連続条件は,
![]() に対して
に対して
で与えられる。運動方程式は式(11.66)を書き直して
である。
ここに![]() は表層の波速で
は表層の波速で
| (11.72) |
と定義した。
まず![]() の運動方程式に式(11.68)の第2式を代入すると,
式(11.67)が求められる。
次に層の中を考えよう。式(11.68)の第1式を式(11.71)に
代入すると
の運動方程式に式(11.68)の第2式を代入すると,
式(11.67)が求められる。
次に層の中を考えよう。式(11.68)の第1式を式(11.71)に
代入すると
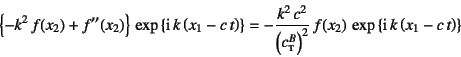
となるので,![]() は
は
を満足しなければならない。
したがって
![]() と求められ
と求められ
を得る。
次に![]() における境界条件にこの解を代入すると
における境界条件にこの解を代入すると
から
を満足しなければならない。
また![]() における連続条件は,式(11.70)に
式(11.68)の第2式と式(11.74)を
代入して,
における連続条件は,式(11.70)に
式(11.68)の第2式と式(11.74)を
代入して,
![]() の係数同士を
比べれば
の係数同士を
比べれば
になる。したがって,式(11.75) (11.76)から![]() を
消去した残りの2式を並べると
を
消去した残りの2式を並べると
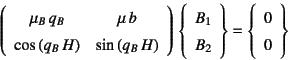
となるから,意味のある![]() ,
, ![]() が存在する条件が
が存在する条件が
となる。これに式(11.67) (11.73)の![]() と
と![]() を
代入して得られる
を
代入して得られる
が,Love波の速さ![]() を決定する方程式になる。
を決定する方程式になる。
![]() のとき
式(11.77)は
のとき
式(11.77)は
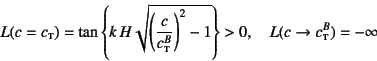
となるので,
![]() に一つの解が
存在することが期待できる。
に一つの解が
存在することが期待できる。
この結果は,いままでの位相速度が持つ特徴とは
かなり違っていることに気付いて欲しい。
平面波やRayleigh波の場合には,位相速度![]() は波の
波数
は波の
波数![]() あるいは周波数
あるいは周波数
![]() とは独立であった。
しかしLove波の場合は,式(11.77)から
明らかなように,
とは独立であった。
しかしLove波の場合は,式(11.77)から
明らかなように,![]() が
が![]() の関数になる。したがって,複数の異なる波数で
できたLove波が伝播するときには,波数毎に異なる位相速度で伝わるため,
最初の波の形が崩れながら移動することになる。
このような波は分散的
であると呼ばれる。
の関数になる。したがって,複数の異なる波数で
できたLove波が伝播するときには,波数毎に異なる位相速度で伝わるため,
最初の波の形が崩れながら移動することになる。
このような波は分散的
であると呼ばれる。