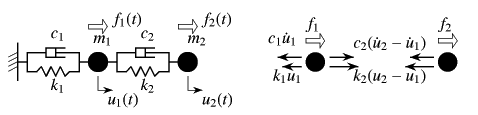 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
1自由度系の節では,振動問題の最も重要な固有振動数を誘導し, 設計に少しだけ関連付けながら,その特徴を示した。 もちろん,社会基盤構造を1質点系で近似するのがかなり乱暴であることは 容易に想像できる。読者の多くは多分,既に有限要素法を知っているから, 任意の初期値境界値問題が多自由度系の問題で近似できることも 知っているだろう。ここでは,その基礎として,複数の 質点から成る多自由度系を対象とし,もう一つの 重要な「振動モード」という概念について説明する。 そのためには,まず運動方程式を誘導する必要があるが, この方程式を求めるという訓練をする場は教育現場にはほとんど無いのが 現実ではないだろうか。文献[136]では,国語という科目が 義務教育以来あって多くの文章を書かされて採点されるにもかかわらず, その書き方を指導する場が一切存在しないことを問題視している。 運動方程式や支配方程式を誘導する技術についても,この国語における 文書作成技術の教育とほぼ同じ状況にある。 振動の運動方程式の誘導は,非常に簡単なNewtonの方程式の誘導に他ならないので, できるだけ答を見ないで各自努力してみて欲しい。 これは,東北大学の故北原道弘教授が振動の授業で学生に期待した事項でもある。 まずは2自由度系から始めよう。
図-10.26は,二つの質点がバネとダッシュポットを
はさんで直列に並んでいる系で,二つの質点が連成(連立)しながら,しかし
自由に動くことができるので,2自由度系と
呼ばれる。同じ図の右に描いた力のダイアグラムから,
質点1に作用している右方向(変位![]() 方向)の
力の総和は
方向)の
力の総和は
である。一方,質点2の場合は
である。したがって,2質点のNewtonの法則は
となる。1自由度系の運動方程式と同じ順番に整理すると
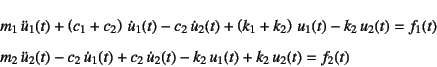
が2自由度系の運動方程式
である。これを1自由度系の運動方程式と同じ形式で行列表示すると
となる。ここに![]() を変位ベクトル,
を変位ベクトル,![]() を
外力ベクトル,
を
外力ベクトル,![]() を質量行列
,
を質量行列
,![]() を減衰行列
,
を減衰行列
,![]() を剛性行列
と呼び
を剛性行列
と呼び
のように定義した。
なお簡単のためにこの章では,括弧無しの太字で行列を表している。
式(10.74)は,時間に関する二つの未知関数の2階の微分方程式なので,
初期条件が四つ必要になる。それは二つの質点の,
それぞれの初期位置と初速の合計四つでいいから
と表すことができる。![]() ,
, ![]() は式(10.75)の
変位ベクトルに対応した初期位置ベクトルと初速ベクトルである。
は式(10.75)の
変位ベクトルに対応した初期位置ベクトルと初速ベクトルである。
最も基本的な振動特性を調べるためには,最初は非減衰の自由振動を
考える必要があるので,![]() と
と![]() を無視した運動方程式
を無視した運動方程式
を対象にしよう。1自由度系の振動解と同じように
と置こう。![]() ,
, ![]() がそれぞれの質点の
振動振幅で,
がそれぞれの質点の
振動振幅で,![]() を振幅ベクトル(この式では複素数と考えておく)と
呼ぶことにする。
式(10.78)を式(10.77)に代入すると
を振幅ベクトル(この式では複素数と考えておく)と
呼ぶことにする。
式(10.78)を式(10.77)に代入すると
が任意の時刻![]() に成立するためには
に成立するためには
でなければならない。これは![]() ,
, ![]() に対する連立方程式であるが,
右辺が零であるから,もし係数の行列が正則であれば振幅ベクトルは零になる。
それは単なる静止状態を意味し,もちろんそれも答の一つだが,
自由振動解析としては欲しい答ではない。
したがって,この2元連立方程式の2式は1次従属の関係になければならないことから
に対する連立方程式であるが,
右辺が零であるから,もし係数の行列が正則であれば振幅ベクトルは零になる。
それは単なる静止状態を意味し,もちろんそれも答の一つだが,
自由振動解析としては欲しい答ではない。
したがって,この2元連立方程式の2式は1次従属の関係になければならないことから
が成立しなければならない。これが固有振動数![]() を決定する
振動数方程式である。つまり
を決定する
振動数方程式である。つまり
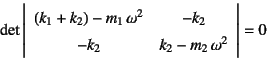
から
あるいは
が,固有振動数![]() を決定する。
を決定する。![]() の解しか意味がないから,
この方程式からは二つの解が求められる。自由度が2になったため,2種類の
固有振動数が存在することを意味する。
そしてその解は
の解しか意味がないから,
この方程式からは二つの解が求められる。自由度が2になったため,2種類の
固有振動数が存在することを意味する。
そしてその解は
![\begin{displaymath}
\omega^2=\dfrac12 \left[
\left\{\left(\dfrac{k_2}{m_2}\righ...
...rac{k_1}{m_1}\right) \left(\dfrac{k_2}{m_2}\right)}
\right]>0
\end{displaymath}](s4img494.gif)
あるいは
となる。ここに
と定義した。![]() の二つの解ともに正である。この二つの解を
小さい方から
の二つの解ともに正である。この二つの解を
小さい方から![]() ,
, ![]() (
(
![]() )と記す。
よくある勘違いに,
)と記す。
よくある勘違いに,
![]() ,
,
![]() と
思い込む人がいるが,そうではないので注意する。
と
思い込む人がいるが,そうではないので注意する。
それぞれの固有振動数に対して,式(10.79)を
満足する![]() と
と![]() の比を求めることができる。
この方程式が1次従属なので,絶対値ではなく,比しか求めることはできない。
例えば2行目の式を用いて
の比を求めることができる。
この方程式が1次従属なので,絶対値ではなく,比しか求めることはできない。
例えば2行目の式を用いて![]() ではないことを期待(いつも
そうなるとは限らないので注意。特に定期試験では。)すると,その比が
ではないことを期待(いつも
そうなるとは限らないので注意。特に定期試験では。)すると,その比が
となるので,それぞれの固有振動数に対して二つの比は
と表すことができる。したがって,二つの質点の変位は
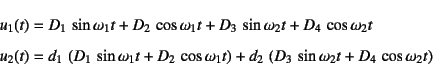
と求められる。積分定数![]() 〜
〜![]() は
初期条件式(10.76)で決める。つまり
は
初期条件式(10.76)で決める。つまり
等と表すこともできる。![]() ,
, ![]() ,
, ![]() ,
, ![]() が積分定数で,
初期条件式(10.76)で決めればいい。この
が積分定数で,
初期条件式(10.76)で決めればいい。この![]() (
(![]() , 2)は
二つの質点の各固有振動数に対応した振動成分の,任意時刻の位置関係を
表しているので,固有振動モード
と呼ばれている。小さい方の振動数に対応したモードを1次モードと呼び,
大きい方が2次モードと呼ばれる。
, 2)は
二つの質点の各固有振動数に対応した振動成分の,任意時刻の位置関係を
表しているので,固有振動モード
と呼ばれている。小さい方の振動数に対応したモードを1次モードと呼び,
大きい方が2次モードと呼ばれる。
では一例として![]() ,
, ![]() の場合を解いてみよう。
ただし,初期条件式(10.76)は
の場合を解いてみよう。
ただし,初期条件式(10.76)は
としておこう。式(10.80)の特性方程式は
となるから,固有振動数はそれぞれ
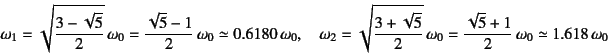
と求められる。それぞれのモード係数![]() は,式(10.84)より
は,式(10.84)より
と求められる。![]() が正なのに対し,
が正なのに対し,![]() は
負であることに注意しよう。図-10.27の左上に,
その二つの質点の位置関係,つまり振動モードを簡単に表示した。
は
負であることに注意しよう。図-10.27の左上に,
その二つの質点の位置関係,つまり振動モードを簡単に表示した。![]() に
対応したモードは,二つの質点が同じ方向に常に移動していることから,
同位相モードと呼ばれる。一方
に
対応したモードは,二つの質点が同じ方向に常に移動していることから,
同位相モードと呼ばれる。一方![]() に対応したモードは逆位相モードと
呼ばれる。簡単のために
に対応したモードは逆位相モードと
呼ばれる。簡単のために![]() 〜
〜![]() を用いた解の表現を用い,それを
初期条件式(
を用いた解の表現を用い,それを
初期条件式(![]() )に代入すると
)に代入すると
となるから
と求められる。したがって,解が
となる。図-10.27の左下の図が,この2質点の
変位の様子である。2種類の振動数で揺れているので,1自由度系より
複雑な動きに見えるかもしれない。そこで,それぞれの質点の変位を,
二つの振動数毎に分けて描いたのが右の二つの図である。
まず小さい振動数の![]() の図(右上)を見ると,二つの
質点が同じ符号で
の図(右上)を見ると,二つの
質点が同じ符号で
![]() の比で運動しているのが明らかである。
これが同位相モードである。一方,大きい振動数の
の比で運動しているのが明らかである。
これが同位相モードである。一方,大きい振動数の![]() の図(右下)を
見ると,お互いがそっぽを向いて
の図(右下)を
見ると,お互いがそっぽを向いて
![]() の比で運動している。
これを逆位相モードと呼ぶのである。この例では,左の図から,あるいは
右2図の縦軸を比較すれば明らかなように,
初期条件の影響を強く受けたため逆位相の2次モードが卓越している。
の比で運動している。
これを逆位相モードと呼ぶのである。この例では,左の図から,あるいは
右2図の縦軸を比較すれば明らかなように,
初期条件の影響を強く受けたため逆位相の2次モードが卓越している。
では,減衰を含む自由振動の場合を考えてみよう。
式(10.74)で外力を無視すれば,運動方程式は
になる。非減衰の場合と同じように
と置く。この場合は振幅ベクトル![]() は複素数である。
というのも,式(10.87)を式(10.86)に代入すると
は複素数である。
というのも,式(10.87)を式(10.86)に代入すると
となるからである。これが任意の時刻![]() に成立するためには
に成立するためには
でなければならない。よって振動数方程式は
となる。1自由度系の結果からも当然なように,
この方程式の解は複素数である。
ただこの方程式は線形代数で習う標準的な固有値問題にはなっていないことから,
自由度が大きくなると固有振動数を求めることは困難になる。
つまり2自由度系の式(10.89)は![]() の複素係数4次方程式で
あることから,電卓と手計算で解を求めることができる限界だろう。
したがって,このような減衰振動については別の解法を用いることにするが,
それについては多自由度系の節-10.2.2で説明する。
の複素係数4次方程式で
あることから,電卓と手計算で解を求めることができる限界だろう。
したがって,このような減衰振動については別の解法を用いることにするが,
それについては多自由度系の節-10.2.2で説明する。
減衰系については,多自由度系の節-10.2.2で
取り扱うことにし,ここでは
もう一つの基本的な状況として,正弦波状の外力が作用したときの強制振動を
解いて,2自由度系の共振曲線を
求めておく。図-10.26には,質点に
直接外力が作用しているものを描いたが,ここの例としては,
支点が正弦波で強制変位させられる図-10.28の
問題の方を解いておこう。図に示した力のダイアグラムから,
二つの質点に作用する右向きの力は,それぞれ
なので,運動方程式は
となる。1自由度系の場合と同様に,相対変位を
と定義して,上の運動方程式を書き直すと
となるので,行列表示すると
となる。![]() と
と![]() は,前述の定義式(10.75)と
同じである。
は,前述の定義式(10.75)と
同じである。
ここでは支点の変位がsine関数で与えられ
で動くものとすると,強制振動解も![]() で振動するだろうから
で振動するだろうから
と置く。式(10.92) (10.93)を式(10.91)に
代入すると
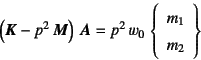
となる。あるいは
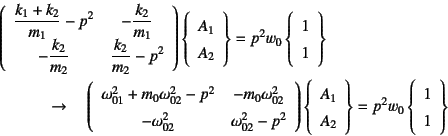
となる。ここでは式(10.83)の記号を用いた。
これを解くと
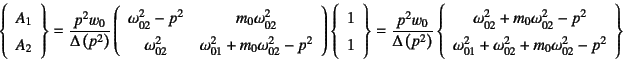
となる。ここに分母は
と置いたが,この式は,式(10.81)の振動数方程式(特性方程式)の
左辺と全く同じなので,固有振動数を![]() ,
, ![]() とすると,
これは
とすると,
これは
と置くことができる。したがって,振幅は
となる。分母から明らかなように,外力の振動数![]() が二つの固有振動数の
いずれかに一致したときに振幅が無限大になる。つまり共振点が
二つ存在することになる。
が二つの固有振動数の
いずれかに一致したときに振幅が無限大になる。つまり共振点が
二つ存在することになる。
前の例と同じように![]() ,
, ![]() の場合の
共振曲線を求めてみる。
固有振動数は,
の場合の
共振曲線を求めてみる。
固有振動数は,
![]() と定義すると
と定義すると
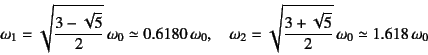
であった。それを用いて,式(10.94)は
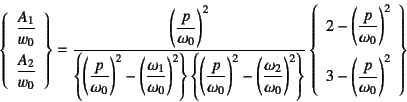
となる。これを図-10.29に示した。![]() が
二つの固有振動数に一致したときに,振幅は無限大になる。
また,上式右辺を見ればわかるように,
質点1は
が
二つの固有振動数に一致したときに,振幅は無限大になる。
また,上式右辺を見ればわかるように,
質点1は
![]() で,
質点2は
で,
質点2は
![]() で
動かなくなる(相対変位なので,支点と一緒に動く)ことも面白い。
で
動かなくなる(相対変位なので,支点と一緒に動く)ことも面白い。
という値をもつときの,固有振動数と固有モードを求めよ。
次に,図-10.31に示したような,
もっと一般的に自由度が![]() の系を考えてみよう。
質点1と質点
の系を考えてみよう。
質点1と質点![]() の力のダイアグラムは2自由度系の2質点と
同じになるので,途中にある
の力のダイアグラムは2自由度系の2質点と
同じになるので,途中にある![]() 番目の質点の力のダイアグラムだけを
同じ図の下に示した。これから
番目の質点の力のダイアグラムだけを
同じ図の下に示した。これから![]() 番目の質点の運動方程式
が
番目の質点の運動方程式
が
となることはわかると思う。したがって,行列表示すると
となる。ここに,
変位ベクトルや外力ベクトル・質量行列・減衰行列・剛性行列は
のように定義すればいい。質量行列
は対角行列になっていて,このような質量行列を集中質量行列
と呼ぶことがある。減衰行列と剛性行列は対称行列で,
かつバンド幅3のバンド行列
(帯行列)でもあることは覚えておくこと。
初期条件については,これも2自由度系と同様
で与えればいい。もちろん![]() も
も![]() も
も![]() 行のベクトルである。
行のベクトルである。
最初は,![]() と
と![]() を無視した,非減衰の自由振動を考えておこう。
変位ベクトルを
を無視した,非減衰の自由振動を考えておこう。
変位ベクトルを
と置いて,運動方程式に代入すると,任意時刻に
でなければならない。これが非零の![]() ,つまり有意な解を持つための
条件が
,つまり有意な解を持つための
条件が
であり,これが振動数方程式(特性方程式)になる。この式から
求められる固有振動数を,
小さい順に並べて![]() (
(![]() , 2,
, 2, ![]()
![]() )とする。
安定な系において固有振動数が
)とする。
安定な系において固有振動数が![]() の実数である
ことの証明は文献[103]にある。
このそれぞれの固有振動数に対応した固有振動モード
を
の実数である
ことの証明は文献[103]にある。
このそれぞれの固有振動数に対応した固有振動モード
を![]() とすると,それは
とすると,それは
を満足する。式(10.100)が成立することから,
この式(10.101)の左辺の係数行列は特異行列である。したがって,
この式は1次従属な関係式だから,![]() は
その成分を唯一には定めることはできず,各要素の比だけを求める
ことができる。したがって,任意の初期値問題の自由振動解(一般解)は
式(10.98)の代わりに
は
その成分を唯一には定めることはできず,各要素の比だけを求める
ことができる。したがって,任意の初期値問題の自由振動解(一般解)は
式(10.98)の代わりに
のような,2種類の未定定数を含む級数表示の形にならざるを得ない。
この複素数の
![]() と
と
![]() ,あるいは実数の
,あるいは実数の![]() と
と![]() を
初期条件式(10.97)で決定すれば,
唯一の自由振動解が求められることになる。
を
初期条件式(10.97)で決定すれば,
唯一の自由振動解が求められることになる。
ところで,固有振動数(固有周期)の大小関係に関しては
を仮定して定義したが,この不等号には等号が無いことを覚えておいて欲しい。
というのも,もしここに等号が成り立ち二つのモードの振動数が
同じになる場合には,それは系の「動的不安定
」を意味するからである。
振動数方程式は,微分方程式の特性方程式と同じものであり,
その二つの特性根が一致する状況は特性根が重根であることを意味する。
その重根に対応した一般解は,
![]() の
形ではなく
の
形ではなく
![]() の
形になることを意味し,それは時間と共に振幅が
無限大になる解,すなわち発散解になる。
動的に不安定な社会基盤構造があってはならないので,
正しく設計された構造系の上式(10.103)の
不等号には等号があってはならないのである。
の
形になることを意味し,それは時間と共に振幅が
無限大になる解,すなわち発散解になる。
動的に不安定な社会基盤構造があってはならないので,
正しく設計された構造系の上式(10.103)の
不等号には等号があってはならないのである。
式(10.95)は連立常微分方程式で,外力が存在する場合に,
そのまま解くのは困難であることはすぐに推測できると思う。
これを比較的容易にする手法に必要な,固有振動モードの重要な特性を
ここで明らかにしておこう。例えば![]() 次と
次と![]() 次の固有振動モード(
次の固有振動モード(![]() )は
それぞれ対応した式(10.101)を満足するから
)は
それぞれ対応した式(10.101)を満足するから
が成立する。この第1式に
![]() を左から乗じ,
第2式に
を左から乗じ,
第2式に
![]() を左から乗じると
を左から乗じると
となる。左の式は第![]() 次の振動モードの運動方程式が第
次の振動モードの運動方程式が第![]() 次モードとする
仮想仕事と考えればいい。
質量行列は対角行列であり,剛性行列は対称行列であることから,
左の式の両辺の項は
次モードとする
仮想仕事と考えればいい。
質量行列は対角行列であり,剛性行列は対称行列であることから,
左の式の両辺の項は
となる。これを上式(![]() )に代入した上で,
二つの式を辺々引き算すると,左辺は同じであることから
)に代入した上で,
二つの式を辺々引き算すると,左辺は同じであることから
となる。式(10.103)で解説したように,安定な構造系であれば
二つの異なる固有振動数は異なる値を持つことから,![]() の
ときには
の
ときには
![]() であり,上式は
であり,上式は
であることを示している。もし質量行列![]() が
単位行列
が
単位行列![]() であれば,この式は,
二つのベクトル
であれば,この式は,
二つのベクトル![]() と
と![]() の内積であり,
それが零になるということは,二つのベクトルが直交していることを
意味する。ここでは,内積を拡張して定義し,質量行列
の内積であり,
それが零になるということは,二つのベクトルが直交していることを
意味する。ここでは,内積を拡張して定義し,質量行列![]() という重みを
含んだ内積
を用いて,二つの固有振動モードは「直交している
」と呼ぶことにしている。
という重みを
含んだ内積
を用いて,二つの固有振動モードは「直交している
」と呼ぶことにしている。
ただし,![]() の時は零にはならないことから
の時は零にはならないことから
のように,新しい量
![]() を定義する。
この
を定義する。
この
![]() は
は![]() 次の固有質量のようなものであるが,
歴史的には一般化された質量
と呼ばれる。また式(10.101)を式(10.105)に
代入すると
次の固有質量のようなものであるが,
歴史的には一般化された質量
と呼ばれる。また式(10.101)を式(10.105)に
代入すると
という関係も成立するため,剛性行列![]() という重みを
含んだ内積に対しても直交性が成立する。
という重みを
含んだ内積に対しても直交性が成立する。![]() は
対角行列ではないので,この内積はかなり一般化されたものであることもわかる。
は
対角行列ではないので,この内積はかなり一般化されたものであることもわかる。
では,任意の初期条件式(10.97)に対して,自由振動解を
求めることを,再度考え直してみよう。どうやら解は,2自由度系の
振動の図-10.27からも予想されるように,![]() 個の
振動モードで揺れて,それが重ね合わされた式(10.102)のような
級数解で表すことができそうだ。そこで解が,時間の未知関数
個の
振動モードで揺れて,それが重ね合わされた式(10.102)のような
級数解で表すことができそうだ。そこで解が,時間の未知関数![]() を
係数とした
を
係数とした
と表現できると仮定してみよう。未知関数![]() が満足すべき
微分方程式は運動方程式から求められるだろうから,
これを運動方程式(10.95)の
非減衰自由振動バージョンの
が満足すべき
微分方程式は運動方程式から求められるだろうから,
これを運動方程式(10.95)の
非減衰自由振動バージョンの
![]() ,
,
![]() の
式に代入すると
の
式に代入すると
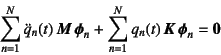
となる。これに左から
![]() を乗じ(つまり
を乗じ(つまり![]() 次
モードとの仮想仕事を算定し),
式(10.105) (10.106)の直交条件を利用すると,
総和のうち
次
モードとの仮想仕事を算定し),
式(10.105) (10.106)の直交条件を利用すると,
総和のうち![]() の項はすべて零になるので
の項はすべて零になるので
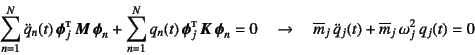
となり,結局,![]() は
は
を満足しないといけないことがわかる。
これは形式的に,1自由度系の非減衰自由振動の運動方程式そのものである。
すなわち![]() 自由度系の問題は,固有振動数とモードさえ算定できていれば
(しかも
自由度系の問題は,固有振動数とモードさえ算定できていれば
(しかも![]() 個全部が求められている必要が無いのもミソ),
個全部が求められている必要が無いのもミソ),![]() 個の
独立した1自由度系の振動問題に置き換えられることを意味する。
したがって解は
個の
独立した1自由度系の振動問題に置き換えられることを意味する。
したがって解は
になる。この積分定数![]() ,
, ![]() を初期条件で決定すればいい。
を初期条件で決定すればいい。
式(10.97)の初期条件式は,級数解で表すと
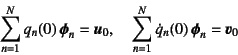
であることから,例えば左から
![]() を
乗じると
を
乗じると
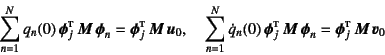
となり,再び直交性の式(10.105) (10.106)を
利用すると,結局
が,それぞれの![]() に対する初期条件になる。この式に
式(10.109)の一般解を代入して,積分定数の
に対する初期条件になる。この式に
式(10.109)の一般解を代入して,積分定数の![]() ,
, ![]() を
決定すれば,唯一の解が求められる。再度,
を
決定すれば,唯一の解が求められる。再度,![]() 次の
次の![]() に
対する初期値問題を整理して書いておくと
に
対する初期値問題を整理して書いておくと
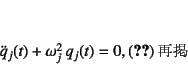
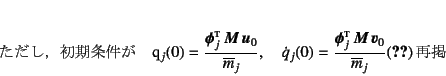
を解けばいいことになる。これは1自由度系の振動問題である。
このように,非減衰自由振動モードを用いて式(10.107)のような
級数解を仮定して初期値問題を解く方法をモード解析法
と呼んでいる。このような問題の![]() は
第
は
第![]() 次モードの振幅であるが,歴史的には一般化された座標
(物理学での名称)と呼ばれている。
連続体の力学に限定すれば,著者としては一般化された変位
と呼びたいところではあるが。
次モードの振幅であるが,歴史的には一般化された座標
(物理学での名称)と呼ばれている。
連続体の力学に限定すれば,著者としては一般化された変位
と呼びたいところではあるが。
ここでは一例として,3質点の自由振動を解いておこう。ただし,
簡単のために![]() ,
, ![]() とする。
また初期条件も簡単のために
とする。
また初期条件も簡単のために
としておこう。そのとき,式(10.99)は
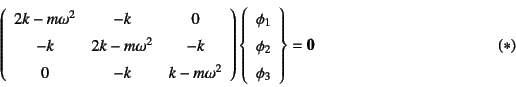
となるから,振動数方程式はこの係数行列の行列式から
となり,固有振動数が
と求められる。3次方程式なので,公式を用いるか,例えば2分法
等で数値的に解ける。
再度上式(![]() )にこれを代入すると,モードが例えば
)にこれを代入すると,モードが例えば
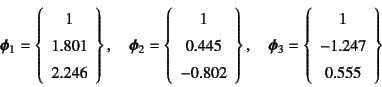
と表現10.10できる。第1次モードはすべてが同じ向きの成分を持っているので 同位相のモードであることがわかる。これに対し,第2次と第3次の モードは,質点の一つが他の二つにそっぽを向いていることから 逆位相のモードになっている。式(10.105)に代入すれば,直交性も 確かめることができる。
さて,この各モードを用い,それぞれの一般化された質量を 式(10.105)で求めると
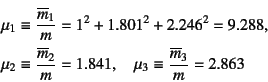
となる。
これを用いて式(10.110)に代入すると,たまたま![]() の
第1成分をすべて1にしておいたため,各モードの
一般化された座標に対する初期条件が
の
第1成分をすべて1にしておいたため,各モードの
一般化された座標に対する初期条件が
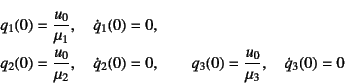
と表される。各モードの一般解は式(10.109)であったから,
この一般解を上の初期条件式に代入すると
と積分定数が求められる。したがって,解は
になる。図-10.32に3質点の変位履歴を示した。 三つの振動数の周期運動の重ね合わせなので,ちょっと見ただけでは 周期運動には見えないのも面白い。
次に,外力が存在する強制振動を解くことを考えよう。
運動方程式は,式(10.95)の減衰項を無視したものになるため
である。ここでもモード解析法を用いてみよう。
つまり,解を自由振動の固有振動モードを用いた級数で
と表現できそうだと仮定して,これを上の運動方程式に代入すると
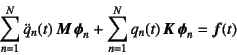
となる。これに左から
![]() を乗じ(つまり
を乗じ(つまり![]() 次モードとの
仮想仕事を算定し),
式(10.105) (10.106)の直交条件を利用すると,
総和のうち
次モードとの
仮想仕事を算定し),
式(10.105) (10.106)の直交条件を利用すると,
総和のうち![]() の項はすべて零になるので
の項はすべて零になるので
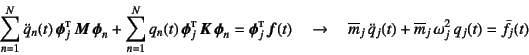
となる。ここに
と定義したものは,外力の第![]() 次モード成分と考えられ,一般化された外力
と呼ばれている。結局
次モード成分と考えられ,一般化された外力
と呼ばれている。結局
を解けば![]() が求められる。これは1自由度系の非減衰強制振動の
運動方程式そのものである。この運動方程式の解は,
右辺の外力
が求められる。これは1自由度系の非減衰強制振動の
運動方程式そのものである。この運動方程式の解は,
右辺の外力![]() に対する特解を
に対する特解を![]() と記すと
と記すと
となるので,これを各モードの初期条件式(10.110)に代入して
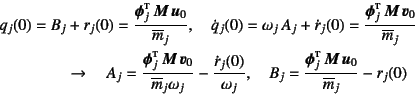
によって,積分定数![]() ,
, ![]() を決定すればいい。
あるいは1自由度系の式(10.48)の単位衝撃応答を利用した,
式(10.49)のDuhamel積分を用いて強制振動解を求めることにすると,
一般解は
を決定すればいい。
あるいは1自由度系の式(10.48)の単位衝撃応答を利用した,
式(10.49)のDuhamel積分を用いて強制振動解を求めることにすると,
一般解は
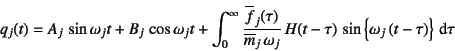
と表すこともできる。Duhamel積分は零初期条件の解なので,
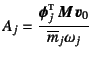 ,
,
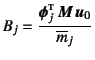 と
なる。
と
なる。
3自由度系の計算は面倒なので演習問題に回すことにし,
ここでは図-10.27で解いた![]() ,
, ![]() の2自由度系の
強制振動を,モード解析法で解いておこう。簡単のために
初期条件と外力条件は
の2自由度系の
強制振動を,モード解析法で解いておこう。簡単のために
初期条件と外力条件は
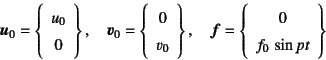
としておく。まず固有振動数は
であり,固有振動モードは
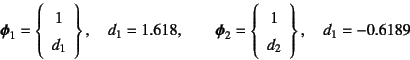
であった。次に一般化された質量と![]() の比を求めると
の比を求めると
となる。初期条件式(10.110)に以上の情報を代入すると
であり,一般化された外力は式(10.113)から
となる。よって,Duhamel積分を用いない場合の一般解は
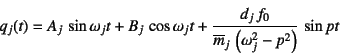
と求められる。これを上の初期条件式に代入すると
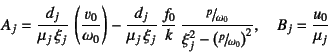
のように![]() ,
, ![]() が求められる。例として
が求められる。例として
の場合の結果を図-10.33に示した。
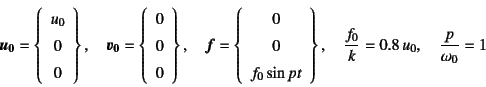
の場合の強制振動解を求めて図示せよ。
では,粘性減衰も含めた式(10.95)を解くことを考えよう。
式(10.107)の形で解を仮定したモード解析法が,
減衰行列を含めた運動方程式にも使えるだろうか。
残念ながら答はもちろん否である。というのも,
モード解析法に使うモードは非減衰自由振動モードであるからだ。
つまりそこには減衰の特性は含まれていないから,
そんなものを使って正しい答が出るはずはないと考えるのが素直である。
それを知りながら,敢えて非減衰自由振動モードを用いようとしたとしても,
式(10.105) (10.106)のような直交性は,
減衰行列に対しては必ずしも成立しないはずである。
したがって,![]() 個の連立微分方程式を,独立した
個の連立微分方程式を,独立した![]() 個の微分方程式に
分解することはできない。もしそのまま解きたい場合には,
次の節で説明する数値的な手法を用いざるを得ないだろう。
しかし機械部品とは異なり,特に社会基盤構造を対象とする場合には幸いなことに,
実は具体的に減衰係数
個の微分方程式に
分解することはできない。もしそのまま解きたい場合には,
次の節で説明する数値的な手法を用いざるを得ないだろう。
しかし機械部品とは異なり,特に社会基盤構造を対象とする場合には幸いなことに,
実は具体的に減衰係数![]() がわかっているわけではない。
したがって,ここではモード解析法が使えるのではないかと期待(近似)して,
その解法をまず説明しよう。すなわち
がわかっているわけではない。
したがって,ここではモード解析法が使えるのではないかと期待(近似)して,
その解法をまず説明しよう。すなわち
が成立することを前提にして定式化してみよう。
ここに
![]() はこの式から求められる定数で,
第
はこの式から求められる定数で,
第![]() 次の見かけ上の減衰定数,あるいは一般化された減衰定数
と呼ばれる。
次の見かけ上の減衰定数,あるいは一般化された減衰定数
と呼ばれる。
最初は,外力![]() が無い自由振動を対象とする。
運動方程式(10.95)の減衰自由振動バージョンの
が無い自由振動を対象とする。
運動方程式(10.95)の減衰自由振動バージョンの
![]() の
式に式(10.107)を代入すると
の
式に式(10.107)を代入すると
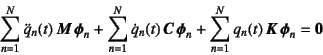
となる。これに左から
![]() を乗じ(つまり
を乗じ(つまり![]() 次モードとの
仮想仕事を算定し),
式(10.105) (10.106) (10.116)の
直交条件を利用すると,総和のうち
次モードとの
仮想仕事を算定し),
式(10.105) (10.106) (10.116)の
直交条件を利用すると,総和のうち![]() の項はすべて零になるので
の項はすべて零になるので
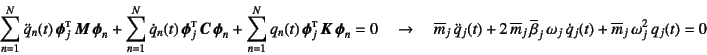
となり,結局
を解けばいいことになる。これは1自由度系の減衰自由振動の運動方程式である。
したがって一般解は
となる。初期条件式(10.110)を用いて積分定数![]() ,
, ![]() を
決定すれば解が決定される。
を
決定すれば解が決定される。
図-10.35 (p.![]() )に
示した破線が,2自由度系で
)に
示した破線が,2自由度系で![]() ,
,
![]() ,
, ![]() とした上で
とした上で
とし,初期条件を
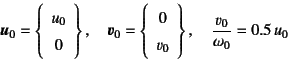
と与えたときの結果である。前節の例の記号を用いれば,
二つの一般化された減衰定数は
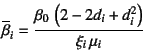
と表現できる。
しかし式(10.116)の「積極的に無視」というのは,
いかに土木屋といえども,
あまり好ましい状況とは思えない。また上述のように社会基盤構造の
場合には,具体的な減衰係数![]() については経験や実測から
求めなければならないのも事実である。
そこで,減衰係数が質量と剛性に比例したものとしてモデル化する
考え方[15]がある。これを比例減衰
あるいはRayleigh減衰
と呼ぶ。それは
については経験や実測から
求めなければならないのも事実である。
そこで,減衰係数が質量と剛性に比例したものとしてモデル化する
考え方[15]がある。これを比例減衰
あるいはRayleigh減衰
と呼ぶ。それは
のようなモデル化である。このようにすれば, 式(10.105) (10.106)で表される 質量行列と剛性行列を通してのモードの直交性から, 減衰行列を通しても自動的にモードが直交することになる。 さて,粘性が弾性や質量に関係があるって本当だろうか。 後述のある種の梁モデルでは,剛性比例にはなることを示すことはできる。
式(10.119)に左右から![]() を乗じると,
を乗じると,
という関係になる。ここでは
式(10.105) (10.106)の関係を用いた。これが,
形式的に式(10.18)の1自由度系の減衰項の
係数の質量倍の
![]() という
表現になって欲しいことから,一般化された比例減衰定数を
という
表現になって欲しいことから,一般化された比例減衰定数を
のように定義すればいいことになる。したがって,減衰定数についても
直交性が成立し
という関係が成り立つ。
この不思議な係数
![]() ,
,
![]() を例えば実測から
決定するには,例えば第
を例えば実測から
決定するには,例えば第![]() 次モードで振動させたときの
減衰定数
次モードで振動させたときの
減衰定数
![]() と第
と第![]() 次モードの
次モードの
![]() とを
測定しておく。これを式(10.120)に代入して連立させ
とを
測定しておく。これを式(10.120)に代入して連立させ
という関係から求めればいい。実際には,三つ以上の振動数に 対する減衰定数を用いて最小2乗法でも使うのではないだろうか。
最後に,外力も含めた運動方程式を,モード解析法で解いておこう。
運動方程式(10.95)に式(10.107)を代入すると
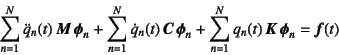
となる。これに左から
![]() を乗じ(つまり
を乗じ(つまり![]() 次モードとの
仮想仕事を算定し),
式(10.105) (10.106) (10.121)の
直交条件を利用すると,総和のうち
次モードとの
仮想仕事を算定し),
式(10.105) (10.106) (10.121)の
直交条件を利用すると,総和のうち![]() の項はすべて零になるので
の項はすべて零になるので
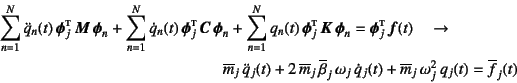
となる。ここに右辺の
![]() は,
式(10.113)で定義した一般化された外力である。結局
は,
式(10.113)で定義した一般化された外力である。結局
を解けばいいことになる。これは1自由度系の減衰強制振動の運動方程式である。
結局,モード解析法を用いさえすれば,本質的には1自由度系の運動方程式を
解くことができればいいことが明らかである。実は,
実際の振動過程を見ると,振動に含まれるすべての成分のうち,
低次の固有振動モードの成分の方が比較的大きくなる。
これは,高周波運動をさせるには大きなエネルギが必要となり,
その逆の現象として,低周波での振動の方が発生し易いからである。
したがって,工学的な観点から社会基盤構造の設計を念頭に置くと,
例えば![]() 自由度系の固有振動数とモードのすべてを知る必要があるわけでは
ないことがわかる。工学的に重要と判断される低次の
自由度系の固有振動数とモードのすべてを知る必要があるわけでは
ないことがわかる。工学的に重要と判断される低次の![]() 個の
固有振動数と固有振動モードを求め,その一般化された
座標を求めてしまえば,必要な精度での近似解を得ることができる。
この
個の
固有振動数と固有振動モードを求め,その一般化された
座標を求めてしまえば,必要な精度での近似解を得ることができる。
この![]() がいくつくらいなら適切かという判断は,
現場の技術者の技量によるのだろう。モードをじっくり考えながら,
どのくらいまでのモードを対象にすればいいのか判断すべきである。
特に梁や柱・骨組のような構造振動の場合には,
振動の仕方についての力学的な予測・判断が非常に重要である。
そういう意味で力学的センスを身に着けることはとても大事である。
なお,減衰強制振動においても非減衰自由振動モードを用いて
モード解析法ができることは,
初期値境界値問題がその固有関数によって解析できることに
通じている。
がいくつくらいなら適切かという判断は,
現場の技術者の技量によるのだろう。モードをじっくり考えながら,
どのくらいまでのモードを対象にすればいいのか判断すべきである。
特に梁や柱・骨組のような構造振動の場合には,
振動の仕方についての力学的な予測・判断が非常に重要である。
そういう意味で力学的センスを身に着けることはとても大事である。
なお,減衰強制振動においても非減衰自由振動モードを用いて
モード解析法ができることは,
初期値境界値問題がその固有関数によって解析できることに
通じている。
ここでは一つの例として,1自由度系の
数値解析法の節でも紹介した中央差分法
を多自由度系に対して適応しておく。
表示を簡単にするために
と定義したとき,速度と加速度は
と近似される。これを運動方程式(10.95)に代入すると
となるので,整理すると
という関係を得,時々刻々の解を求めることができる。
また,一番最初のステップの![]() については,
式(10.124)の関係から
については,
式(10.124)の関係から![]() を消去して得る
を消去して得る
を時刻![]() で表現し,さらに
で表現し,さらに![]() の瞬間の運動方程式から得る
の瞬間の運動方程式から得る
という関係を上の式の右辺第3項に代入すれば
から,時刻![]() の
の![]() を
算定できる。
を
算定できる。![]() は
は![]() の
単位行列である。図-10.53にフローチャートを
示した。図-10.35には,節-10.2.2
(6)で例題とした2自由度系を
モード解析法で解いた厳密解(破線)との比較を示した。
この例は,
の
単位行列である。図-10.53にフローチャートを
示した。図-10.35には,節-10.2.2
(6)で例題とした2自由度系を
モード解析法で解いた厳密解(破線)との比較を示した。
この例は,
![]() と
したときの時間ステップを
と
したときの時間ステップを
![]() とした場合の結果である。
これを
とした場合の結果である。
これを
![]() にすると,数値解は厳密解とほとんど
重なってしまう。数値解の安定性のためには,時間ステップは
にすると,数値解は厳密解とほとんど
重なってしまう。数値解の安定性のためには,時間ステップは
である必要[8]がある。ここに![]() は最小固有周期である。
この例の場合の条件は
は最小固有周期である。
この例の場合の条件は
![]() 程度で
あった。つまり自由度
程度で
あった。つまり自由度![]() が大きくなると,時間ステップを非現実的なくらい小さく
しなければならないことを示している。もっと良好な安定性や正確性を有する
他の手法には,例えばNewmark法やWilsonの
が大きくなると,時間ステップを非現実的なくらい小さく
しなければならないことを示している。もっと良好な安定性や正確性を有する
他の手法には,例えばNewmark法やWilsonの![]() 法等があるが,
それについては文献[8]を参照のこと。
法等があるが,
それについては文献[8]を参照のこと。