 |
�ŐV�ł𐳊m�ɓǂޏꍇ�ɂ� pdf �t�@�C�� ���ǂ����B����� web �����̂��߂̊ȈՋ��łł��B
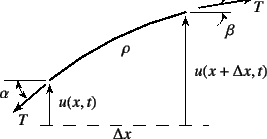
�����܂ł́C���U�I�ɕ��z���鎿�_���o�l��_�b�V���|�b�g�Ō�������Ă��� �n��ΏۂƂ��Ă����B�������C�g�̉��ɁC���邢�͎Љ��Ս\���ɂ́C ���ʂ����U�I�ɕ��z���Ă��邻���������n�͂قƂ�nj�������Ȃ��B ���ۂ̍\���́C�A���I�ɕ��z�������ʂ����A���̂Ƃ��đ����Ȃ���Ȃ�Ȃ����Ƃ� ���炩�ł��낤�B�����C�U�����[�h�Ƃ������T�O�́C�A���I�ȕ��z���ʌn�ł� ���ɏd�v�ȊT�O�ł���B�����ł́C�g������������n�̐U����͂̊�{�Ƃ��āC �܂��Ȃ������̖����n�̐U�����������B
����Β����ɗp�����Ă���P�[�u���͌��Ƃ��ă��f�����ł��������B
���́C�\�ߑ傫�Ȓ��͂ň������ď��߂Ĉ��肷��\���ł���B
�����ł��d�͂̉e���͖������i�荇���Ă����Ԃ���̕ϓ��݂̂�
�ΏۂƂ��j�C�x�z��������U�����Ă����B
�܂������Ȍ����U�����ĕψʂ�������u�Ԃ̐}-10.36�ŁC
�㉺�����̉^����������
�ƂȂ�B![]() �͌��̖��x�ŁC
�͌��̖��x�ŁC![]() �͌��̒f�ʐςł���B
���̕ψʂ��\���������ꍇ�ɂ́C�w�I�ȊW����
�͌��̒f�ʐςł���B
���̕ψʂ��\���������ꍇ�ɂ́C�w�I�ȊW����
�ƂȂ�B������㎮�ɑ�����Đ��������
�ƂȂ�B���邢��
�ƂȂ�B������![]() �͔g�̑��x�i�ʑ����x�j�ł���B
���邢�͎�(10.130)���g��������
�Ƃ��Ă��B
�͔g�̑��x�i�ʑ����x�j�ł���B
���邢�͎�(10.130)���g��������
�Ƃ��Ă��B
�����ł͒���![]() �̗��[���Œ肳�ꂽ���̐U��������ΏۂƂ���̂ŁC
���E�����͗��[��
�̗��[���Œ肳�ꂽ���̐U��������ΏۂƂ���̂ŁC
���E�����͗��[��
�Ɨ^�����邱�ƂɂȂ�B���������ɂ��ẮC
���Ԃɂ��Ă�2�K�̔����������Ȃ̂ŁC�����`��Ə�����
�̂悤�ɗ^��������B
�����ł͕ϐ������ʼn������߂Ă݂悤�B�܂�
�ƒu���C�^��������(10.130)�ɑ�����Đ��������
�ƂȂ�B�v���C����![]() �Ɋւ��������\���B���̎���
�C�ӂ̏ꏊ
�Ɋւ��������\���B���̎���
�C�ӂ̏ꏊ![]() �Ǝ���
�Ǝ���![]() �Ő������Ȃ���Ȃ�Ȃ����C���ӂ�
�Ő������Ȃ���Ȃ�Ȃ����C���ӂ�![]() �݂̂�
���ł���C�E�ӂ�
�݂̂�
���ł���C�E�ӂ�![]() �݂̂̊��ɂȂ��Ă���C���̓�������������̂�
���̗��ӂƂ��ɒ萔�ł���Ƃ��݂̂ł���B�܂�
�݂̂̊��ɂȂ��Ă���C���̓�������������̂�
���̗��ӂƂ��ɒ萔�ł���Ƃ��݂̂ł���B�܂�
�ƒu�������̂�
���Ɨ����Đ������Ȃ���Ȃ�Ȃ��B���E�������ϐ���������ƁC
�C�ӂ̎����ł��ꂪ�������Ȃ���Ȃ�Ȃ��̂�
�ƂȂ�B���������͕����ł��Ȃ��̂ŁC���炭���u���Ă������B
�^���������Ƌ��E���������������ł����̂ŁC
��(10.133)��![]() �̕���
��ɉ����������B�܂�
�̕���
��ɉ����������B�܂�![]() �̏ꍇ��
�̏ꍇ��![]() ��
�u���ƁC��ʉ���
��
�u���ƁC��ʉ���
�ƂȂ�̂ŁC���E������(10.134)�ɑ�������
����ϕ��萔�����߂邱�ƂɂȂ�B������![]() �ŁC
���̂Ƃ�
�ŁC
���̂Ƃ�![]() �͏�ɐ��Ȃ̂ŁC
����
�͏�ɐ��Ȃ̂ŁC
����![]() ,
, ![]() �݂̂����ƂȂ�C�Ӗ��̂���
�݂̂����ƂȂ�C�Ӗ��̂���![]() �͑��݂��Ȃ����ƂɂȂ�B
�ł͎���
�͑��݂��Ȃ����ƂɂȂ�B
�ł͎���![]() �̏ꍇ���l����ƁC��ʉ���
�̏ꍇ���l����ƁC��ʉ���
![]() �ƂȂ�̂ŁC
���E������
�ƂȂ�̂ŁC
���E������![]() ,
, ![]() ��v�����C������Ӗ��̂�����ɂ͂Ȃ�Ȃ��B
����������
��v�����C������Ӗ��̂�����ɂ͂Ȃ�Ȃ��B
����������![]() �͕��łȂ���Ȃ�Ȃ����Ƃ��킩��B
�͕��łȂ���Ȃ�Ȃ����Ƃ��킩��B
�ł�
![]() �ƒu���ƁC��ʉ���
�ƒu���ƁC��ʉ���
�ƂȂ�C���E��������
��B������![]() ����ɂȂ�Ȃ����߂ɂ�
����ɂȂ�Ȃ����߂ɂ�
�łȂ���Ȃ�Ȃ��B����������![]() �͕s��ɂȂ�C����
�͕s��ɂȂ�C����
�Ƌ��߂���B�ŏI�I�Ɏ�(10.133)��![]() ��
�����������ɁC��(10.135)��
��
�����������ɁC��(10.135)��![]() �������ĉ�����
�������ĉ�����
�����ł���B���̌`���ŗL�U����![]() ��sine, cosine����
�Ȃ邱�Ƃ���C���̐U���̌ŗL�U����
��sine, cosine����
�Ȃ邱�Ƃ���C���̐U���̌ŗL�U����![]() ��
��
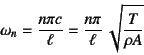
�ƂȂ�B�܂�C��������d���������͐U�������������Ȃ�̂ŁC����
�Ⴍ�Ȃ�B����C���̋t�ɂ��邩�C���͂�傫������ƁC���͍����Ȃ�B
�O�����h�s�A�m�̊W���J���Ă݂ė~�����B
�Ⴂ���̃s�A�m���͑��������Ȃ��Ă��邵�C
�������̃s�A�m���ׂ͍��Z���Ȃ��Ă���B
�����i�`���[�j���O�j�ł͌��̒���![]() ������B
������B
������x![]() �����߂�v���Z�X�������ƁC�����ׂ�����
�����߂�v���Z�X�������ƁC�����ׂ�����
�ƕ\�����Ƃ��ł���B�����
![]() �����̈�ł���C
�����������ŕ\���ꂽ�ŗL�l���ɂȂ��Ă���B
�����̈�ł���C
�����������ŕ\���ꂽ�ŗL�l���ɂȂ��Ă���B![]() ���ŗL��
�ƌĂ�C
���ŗL��
�ƌĂ�C![]() ���邢��
���邢��![]() ���ŗL�l�ł���B
�����I�Ȍ��t���g���Ȃ�C
���ŗL�l�ł���B
�����I�Ȍ��t���g���Ȃ�C![]() ���ŗL�U�����[�h
�ł���C
���ŗL�U�����[�h
�ł���C
![]() ���ŗL�U�����ł���B�A���̂̏ꍇ�́C
��(10.136)�̂悤�ɖ����̌ŗL��������C
���̂��ׂĂ����̌��ł���B�ŗL�l������ɑΉ����Ė�������B
�����ő����R�x�n�̐U���������Ƃ��̃��[�h��͖@���v���o���Ă݂悤�B
���[�h��͖@�ł́C�܂����R�U����͂�����
�ŗL�U�����[�h�i�ŗL�x�N�g���j�ƌŗL�U�����i�ŗL�l�j��
���߁C���̃��[�h��p���ĉ����������ʼn��肵�C�������߂悤�Ƃ����B
���̏ꍇ�����l�ɁC�㎮(10.137)�̌ŗL�l����������
�ŗL���ƌŗL�l�����߂邱�Ƃ��ł����B���������āC�����R�x�n�̉���
�\����(10.107)���g����
���ŗL�U�����ł���B�A���̂̏ꍇ�́C
��(10.136)�̂悤�ɖ����̌ŗL��������C
���̂��ׂĂ����̌��ł���B�ŗL�l������ɑΉ����Ė�������B
�����ő����R�x�n�̐U���������Ƃ��̃��[�h��͖@���v���o���Ă݂悤�B
���[�h��͖@�ł́C�܂����R�U����͂�����
�ŗL�U�����[�h�i�ŗL�x�N�g���j�ƌŗL�U�����i�ŗL�l�j��
���߁C���̃��[�h��p���ĉ����������ʼn��肵�C�������߂悤�Ƃ����B
���̏ꍇ�����l�ɁC�㎮(10.137)�̌ŗL�l����������
�ŗL���ƌŗL�l�����߂邱�Ƃ��ł����B���������āC�����R�x�n�̉���
�\����(10.107)���g����
�Ɖ��肵�āC�����������Ƃ��l���Ă݂�B
�܂������R�x�n�̃��[�h��͖@�ŏd�v�ȓ����ł�����
�ŗL�U�����[�h�i�x�N�g���j�̒��𐫂��v���o���āC
���̌ŗL�U�����[�h�i���j�̒��𐫂ɂ��Ċm�F���悤�B
����![]() ���̌ŗL��
���̌ŗL��![]() �́C��(10.137)����
�́C��(10.137)����
��������B
���[�h�̒��𐫂�������Ƃ��ɂ́C�ʂ̃��[�h�����z�ψʂ�
�l���ĉ��z�d�����Z�肵�Ă݂邱�Ƃ���n�߂Ă����B�����ł�
�����A�v���[�`�����Ă݂�B�܂�㎮��![]() ���悶�āC
�S�̈�ϕ�����C���S�̂̉��z�d���ɂȂ�B
�܂�C���̉��z�d������
���悶�āC
�S�̈�ϕ�����C���S�̂̉��z�d���ɂȂ�B
�܂�C���̉��z�d������
�ƂȂ�B��1�����ϕ������
�ƂȂ邩��C���E������(10.137)�ŗ��[�̍��������C���Ǐ㎮��
�Ƃ������z�d��������������B
�����v���Z�X���![]() �����[�h�̕������ɓK�p���邽�߂ɁC
�ŗL��
�����[�h�̕������ɓK�p���邽�߂ɁC
�ŗL��![]() ������ɏ悶�ĉ��z�d���������߂��
������ɏ悶�ĉ��z�d���������߂��
�ɂȂ�B����2����ӁX���������ƁC��1���͓����Ȃ̂ŏ����Ă��܂�
�ƂȂ�B��(10.137)���疾�炩�Ȃ悤�ɁC�قȂ�ŗL�l���m��
�قȂ�l�ɂȂ�̂ŁC���̖��̌ŗL����
�Ƃ��������������Ă���B���̍��ӂ��̊������� �ƌĂ�ł���B�����āC��̈قȂ���̓��ς���ɂȂ邱�Ƃ���C ���������m�͒������Ă����Ə̂���̂ł���B ���̂悤������ �́C���[�h��͖@�ɂƂ��čł��d�v�ȓ����ł���B
�ł́C��(10.138)�̋��������^��������(10.130)��
��������
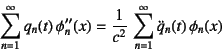
�ƂȂ�̂ŁC��(10.139)�����ӂɑ�������
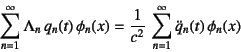
����������B���̎��Ƒ�![]() ���̌ŗL���Ɠ��ρi���z�d���j���Ƃ�ƁC
���ǒ��𐫂̎�(10.140)�ɂ���āC�����a�̑�
���̌ŗL���Ɠ��ρi���z�d���j���Ƃ�ƁC
���ǒ��𐫂̎�(10.140)�ɂ���āC�����a�̑�![]() ������
�ȊO�͂��ׂė�ɂȂ�
������
�ȊO�͂��ׂė�ɂȂ�
���C�W��![]() �����肷��������ɂȂ�B���̈�ʉ���
�����肷��������ɂȂ�B���̈�ʉ���
�Ƌ��߂���B���������āC���̖��̈�ʉ���
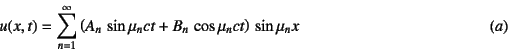
�ƂȂ�B
�Ō�ɁC���̈�ʉ��̎�(![]() )������������(10.132)��
��������
)������������(10.132)��
��������
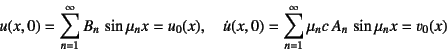
�ƂȂ�B�ēx�C��![]() ���̌ŗL���Ƃ̓��ς��Ƃ��
���̌ŗL���Ƃ̓��ς��Ƃ��
�ƂȂ邱�Ƃ���C�ϕ��萔��
�Ƌ��߂���B
����[62]�ɂ������]�L���Ă����B
���̒�����![]() �����܂ݏグ�C�������Ǝ�𗣂����Ƃ���
�U�������߂Ă݂�B����������
�����܂ݏグ�C�������Ǝ�𗣂����Ƃ���
�U�������߂Ă݂�B����������
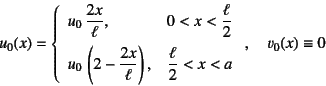
�̂悤�ɏ������Ƃ��ł���B�������(![]() )��
�������C�ϕ��萔�����߂邱�Ƃ��ł��C����
)��
�������C�ϕ��萔�����߂邱�Ƃ��ł��C����
�ƂȂ�B�����}-10.37�Ɏ������B �j���͋�����40����p�������ŁC������5���݂̂ŕ`�������ł���B ���Ȃ������ł���r�I�����������߂��Ă���B �������͎��̐߂̐}-10.38�Ɏ������悤�ɁC �O�p�`���`�̂悤�ȋ敪�I�Ȓ����ł���B
������x�C��ʉ��̎�(![]() )�߂Ă݂悤�B
�������������������
)�߂Ă݂悤�B
�������������������
![\begin{eqnarray*}
&&u(x,t)=\sum_{n=1}^\infty \left(A_n \sin \mu_n ct+B_n \cos ...
...ight)\right\}
+\sin\left\{\mu_n\left(x+ct\right)\right\}\right]
\end{eqnarray*}](s4img771.gif)
�ƂȂ邱�Ƃ���C����![]() �Ƃ�������
�Ƃ�������![]() �Ƃ�������
�Ƃ�������
�̂悤�ɕ\����Ă��邱�Ƃ��킩��B
�ł�![]() �Ƃ������͂ǂ����������ۂ�\���Ă��邾�낤���B
�Ⴆ���鎞��
�Ƃ������͂ǂ����������ۂ�\���Ă��邾�낤���B
�Ⴆ���鎞��![]() �ɂ���ꏊ
�ɂ���ꏊ![]() �ŁC���̊���
�ŁC���̊���![]() �Ƃ���
�l�������Ă����Ƃ���B���ꂩ��
�Ƃ���
�l�������Ă����Ƃ���B���ꂩ��![]() ���Ԃ�
�o����
���Ԃ�
�o����
![]() �̂Ƃ��́C
�̂Ƃ��́C
![]() �Ƃ����ꏊ��
���̊��̒l��
�Ƃ����ꏊ��
���̊��̒l��
�ƂȂ�B
�܂�C![]() ,
, ![]() �ɂ�����u������ԁv�����̂܂�
�ɂ�����u������ԁv�����̂܂�![]() ��
��![]() ��
�ώ@���ꂽ���ƂɂȂ�B���������āC
��
�ώ@���ꂽ���ƂɂȂ�B���������āC![]() �Ƃ������́C
�u
�Ƃ������́C
�u![]() �̐��̕�����
�̐��̕�����![]() �œ`�d�����v�������ۂ�\���Ă���B
���l�ɁC
�œ`�d�����v�������ۂ�\���Ă���B
���l�ɁC![]() �́C
�u
�́C
�u![]() �̕��̕�����
�̕��̕�����![]() �œ`�d�����v�������ۂ�\���B
���������Č��̐U�����́C���̕�����
�œ`�d�����v�������ۂ�\���B
���������Č��̐U�����́C���̕�����![]() �œ`�d����g�ƁC
���̕�����
�œ`�d����g�ƁC
���̕�����![]() �œ`�d����g�̏d�ˍ��킹�Ɖ��߂��Ă��������Ƃ�
�Ȃ�B�}-10.38�ɂ́C�O�߂ň��������́C
�������܂ݏグ�ė������ꍇ�́C�g���̉��̎�(
�œ`�d����g�̏d�ˍ��킹�Ɖ��߂��Ă��������Ƃ�
�Ȃ�B�}-10.38�ɂ́C�O�߂ň��������́C
�������܂ݏグ�ė������ꍇ�́C�g���̉��̎�(![]() )�̖͎��}���������B
�E�ɑ��x
)�̖͎��}���������B
�E�ɑ��x![]() �œ`�d��������ƍ��ɓ`�d����j���̏d�ˍ��킹�����ɂ���}��
���ł���C�����̎O�p�`����`�ɂȂ�C���̍��������X�ɕω����Ă����̂�
�����ł���B
���̂悤�ɁC�g���ƐU���͓������ۂł���C���̊ώ@�̎d����ς���������
���邱�Ƃ��킩��B
���������āC��(10.130)�͔g���������Ƃ��Ă�Ă���̂��B
�œ`�d��������ƍ��ɓ`�d����j���̏d�ˍ��킹�����ɂ���}��
���ł���C�����̎O�p�`����`�ɂȂ�C���̍��������X�ɕω����Ă����̂�
�����ł���B
���̂悤�ɁC�g���ƐU���͓������ۂł���C���̊ώ@�̎d����ς���������
���邱�Ƃ��킩��B
���������āC��(10.130)�͔g���������Ƃ��Ă�Ă���̂��B
�Ō�ɁC���[�h��͖@�Ƃ����ϓ_����C�����R�x�n�ƌ����r���Ă����B
�܂��ŗL�l����
�ƕ\�����B�ŗL�x�N�g���ƌŗL���́C���̂悤�ȓ��ςɑ���
����
�������Ă��邱�Ƃ���C��������x�N�g���C���邢�͒�������
���̏W���ł���B�����ĉ���
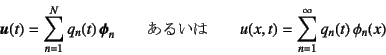
�Ɖ��肵�Ė����������Ƃ��Ă���B
�A���͖̂����̎��R�x�����ƍl�����邱�Ƃ���C���������������ɂȂ��Ă���B
�����Ĉ�ʉ����ꂽ���W�ƌĂ�ł�����![]() �́C���ꂼ��
�́C���ꂼ��
���������Ƃɂ���ċ��߂���B����͌�������C1���R�x�n�� �^���������ł���B�ŏI�I�ɁC�ϕ��萔�͏����������� ���肷�邱�Ƃ��ł��C���̍ۂɂ��d�v�Ȑ��������������ł���B
���Ƃ����̂͌���2�����I�Ɋg�������悤�Ȃ��̂ŁC�������r�I
�傫�Ȉ����蒣�͂�^���Ă����Ȃ��ƁC����ȍ\���ɂ͂Ȃ�Ȃ��B
�����ł́C���܂�Љ��Ս\���ł͎g��Ȃ����C�h�[���̓V���
�v���邽�߂̓��̑̑���
���邽�߂ƁC������Fourier�����͕K�������O�p���ɂ��
���������ł͂Ȃ����Ƃ��������߂ɁC�~�`���̐U�����l���Ă݂�B
���̉^���������́C��(10.130)��2�����Ɋg������
�ɂȂ邱�Ƃ́C�����ɐ����ł���Ǝv���B![]() ��
��͂蒣��
��
��͂蒣��![]() �Ɩ��x
�Ɩ��x![]() �Œ�`���ꂽ�ʑ����x�ł���B���������ł́C
�~�`�̈�̖���ΏۂƂ��Ă��邱�Ƃ���C���p���W�ł͂Ȃ��C
�ɍ��W�ŕ\�����������������Ƃ��e�Ղɐ����ł���B
�ɍ��W�ł̃��v���V�A����
�Œ�`���ꂽ�ʑ����x�ł���B���������ł́C
�~�`�̈�̖���ΏۂƂ��Ă��邱�Ƃ���C���p���W�ł͂Ȃ��C
�ɍ��W�ŕ\�����������������Ƃ��e�Ղɐ����ł���B
�ɍ��W�ł̃��v���V�A����
�ƂȂ邱�Ƃ́C���w�̖{������킩��̂ŁC���ǁC
���̉^��������
��
�ƂȂ�B![]() �͖��̊O�a�ł���B���E�����́C���͂��Œ肳��Ă�����̂Ƃ���
�͖��̊O�a�ł���B���E�����́C���͂��Œ肳��Ă�����̂Ƃ���
�ƂȂ邪�C�^��������(10.142)��![]() �œ��قɂȂ�i���ꂪ
��ɂȂ�j���Ƃ��l�����āC�~�`���̒����Łu�������Ȃ��Ɓv���N���Ȃ����Ƃ�
�����ɂ��邽�߂�
�œ��قɂȂ�i���ꂪ
��ɂȂ�j���Ƃ��l�����āC�~�`���̒����Łu�������Ȃ��Ɓv���N���Ȃ����Ƃ�
�����ɂ��邽�߂�
��t�ѓI�ȏ����Ƃ��Ă����B�������C
�������a��![]() �̃h�[�i�c��̖���ΏۂƂ���ꍇ�ɂ́C
��(10.144)�̕t�я����̑����
�̃h�[�i�c��̖���ΏۂƂ���ꍇ�ɂ́C
��(10.144)�̕t�я����̑����
![]() ��
�Ȃ邱�Ƃɂ͒��ӂ��ė~�����B����ɁC���͐܂�Ȃ�������j�ꂽ�肵�Ȃ���
�A�������܂܂ł��邩��C�Ⴆ��
��
�Ȃ邱�Ƃɂ͒��ӂ��ė~�����B����ɁC���͐܂�Ȃ�������j�ꂽ�肵�Ȃ���
�A�������܂܂ł��邩��C�Ⴆ��![]() �ɂ�����
�ɂ�����
�Ƃ����A���������ۂ����Ƃɂ���B���������́C����![]() �ɂ�����
�����`��Ə�����^�����������
�ɂ�����
�����`��Ə�����^�����������
�Ɨ^��������̂Ƃ���B
���̏ꍇ�Ɠ��l�ɕϐ�������������߂邱�Ƃ��ł��邪�C
���̌ŗL�l���̊g������C�ł��d�v�ȌŗL�l����
�ƂȂ肻���Ȃ��Ƃ́C�����Ɨe�Ղɐ����ł���Ǝv���B
![]() ��
�ŗL�U�����[�h
�ł���B�^����������l�͕ϐ����������Ă݂ė~�����B
��
�ŗL�U�����[�h
�ł���B�^����������l�͕ϐ����������Ă݂ė~�����B![]() ���萔�ł���B
�����ł���ɕϐ�����������
���萔�ł���B
�����ł���ɕϐ�����������
���㎮�ɑ�����Đ��������
���������Ȃ���Ȃ�Ȃ����Ƃ��킩��B
�v���C���́C���ꂼ������ɂ��Ă̔����ł���B
�܂�![]() ��
��![]() �ɂ������ŁC
�ɂ������ŁC
![]() ��
��![]() �ɂ������ł���B
���ꂩ��C���ꂼ��ɂ��Ă̔�����������
�ɂ������ł���B
���ꂩ��C���ꂼ��ɂ��Ă̔�����������
�ƕ\���ł���B����C���E������(10.143) (10.144)
(10.145)�́C![]() �ɂ��Ă�
�ɂ��Ă�
�ł���C![]() �ɂ��Ă�
�ɂ��Ă�
�ƂȂ�B
�܂�
![]() �́C����������(10.149)�߂���ŁC
���E������(10.151)���������ł��邱�Ƃ�v������̂ŁC
�Œ���C���̒萔
�́C����������(10.149)�߂���ŁC
���E������(10.151)���������ł��邱�Ƃ�v������̂ŁC
�Œ���C���̒萔![]() �͐��łȂ���Ȃ�Ȃ����Ƃ����炩�ł���B
�܂��C���̉���
�͐��łȂ���Ȃ�Ȃ����Ƃ����炩�ł���B
�܂��C���̉���![]() �����łȂ�����
���E�����i
�����łȂ�����
���E�����i![]() �����̘A�������j��(10.145)�����Ȃ��̂ŁC
����
�����̘A�������j��(10.145)�����Ȃ��̂ŁC
����![]() �͔̐���
�͔̐���
�łȂ���Ȃ炸�C�Ή�����ŗL����
�ƂȂ�B![]() ���܂ނ��Ƃɒ��ӂ���B
���܂ނ��Ƃɒ��ӂ���B
����![]() ��
��![]() �̕�����(10.149)�ɑ�������
�̕�����(10.149)�ɑ�������
��![]() �����߂�����������ɂȂ�B
�܂�
�����߂�����������ɂȂ�B
�܂�![]() �̕������������邽�߂ɁC
�܂����ꂪ��(
�̕������������邽�߂ɁC
�܂����ꂪ��(![]() )�ł���Ɖ��肵�Ă݂�B
�����Ŏ�(10.154)��
)�ł���Ɖ��肵�Ă݂�B
�����Ŏ�(10.154)��![]() ��
���������̂�
��
���������̂�![]() ���悶�āC
���悶�āC![]() ����
����![]() �܂Őϕ�����B�܂�
�܂Őϕ�����B�܂�
�����藧�B�E�ӂ̔�ϕ����͔Ȃ̂ŁC�ϕ��l���ɂȂ�B
������ӂɂ��ẮC�����ϕ������ċ��E�������l�������
�ƂȂ�B���ǁC��(![]() )�̍��ӂ͕��ŁC�E�ӂ͔ɂȂ邱�Ƃ���C
�����(
)�̍��ӂ͕��ŁC�E�ӂ͔ɂȂ邱�Ƃ���C
�����(![]() )���������Ȃ����Ƃ��킩��B
�����
)���������Ȃ����Ƃ��킩��B
�����
![]() �ƒu�����B
��������ƁC
�ƒu�����B
��������ƁC![]() �ɂ��Ă̔����������́C��(10.154)����
�ɂ��Ă̔����������́C��(10.154)����
�ƂȂ�B���̎���Bessel�̔����������ƌĂ�C����Bessel��
��
�ƕ\�����邱�Ƃ������B![]() ��
��![]() ���̑�1��Bessel���C
���̑�1��Bessel���C![]() ��
��![]() ����
��2��Bessel���ƌĂ��B���ꂼ��̗��}-10.39��
�������B
����
��2��Bessel���ƌĂ��B���ꂼ��̗��}-10.39��
�������B
�������C���E������(10.150)�́C![]() �ɂ�����L�E����
�v�����Ă��邱�Ƃ���C�}��������炩�Ȃ悤�ɁC
��2���Bessel���͉��̌��ɂ͂Ȃ�Ȃ��B
�������C�h�[�i�c��̖��̏ꍇ��
�ɂ�����L�E����
�v�����Ă��邱�Ƃ���C�}��������炩�Ȃ悤�ɁC
��2���Bessel���͉��̌��ɂ͂Ȃ�Ȃ��B
�������C�h�[�i�c��̖��̏ꍇ��![]() ���܂܂Ȃ��̂ŁC��2���Bessel����
���ɂ͂Ȃ�B���������āC�����̉~�`���̏ꍇ�ɂ́C
���܂܂Ȃ��̂ŁC��2���Bessel����
���ɂ͂Ȃ�B���������āC�����̉~�`���̏ꍇ�ɂ́C![]() ��
��
�����ɂȂ�B����ɁC����̋��E������(10.150)����
���������Ȃ���Ȃ�Ȃ��B���̏�����
�ŗL�l![]() �����肷��B�}-10.39����
�e�Ղɐ����ł���悤�ɁCBessel���́C�������ł͂Ȃ����̂�
�����I�ɗ���܂������ŁC��_�͖������݂���B���������āC
�㎮(
�����肷��B�}-10.39����
�e�Ղɐ����ł���悤�ɁCBessel���́C�������ł͂Ȃ����̂�
�����I�ɗ���܂������ŁC��_�͖������݂���B���������āC
�㎮(![]() )������
)������![]() �͂��ꂼ���
�͂��ꂼ���![]() �ɑ��Ė�����
���݂���B���������āC�����1�ڂ���
�ɑ��Ė�����
���݂���B���������āC�����1�ڂ���![]() , 2,
, 2, ![]() �ƋL�����Ƃ�
���āC
�ƋL�����Ƃ�
���āC![]() �Ƃ����ŗL�l��
�Ƃ����ŗL�l��
�����Ă�����̂Ƃ��ċ��߂���B�\-10.1�ɋ�̓I��
��_��������C�����p����ƗႦ��
�̂悤�Ȓl��![]() �͎����ƂɂȂ�B���������āC
�ŗL��
�͎����ƂɂȂ�B���������āC
�ŗL��![]() �̉��͍ŏI�I��
�̉��͍ŏI�I��
�ƂȂ�BBessel�����������ł͂Ȃ����Ƃ���C![]() ���Ⴆ��
���Ⴆ��![]() ��
�����{�̂悤�ȕ\���ɂ͂Ȃ�Ȃ����Ƃɒ��ӂ��ė~�����B
��
�����{�̂悤�ȕ\���ɂ͂Ȃ�Ȃ����Ƃɒ��ӂ��ė~�����B
�܂���(10.153)�̌ŗL��
![]() �́C�O�߂̌���
�ꍇ�̓���������e�Ղɗ\�z�ł���悤�ɁC
�́C�O�߂̌���
�ꍇ�̓���������e�Ղɗ\�z�ł���悤�ɁC![]() �ɑ��Ē���
�ɑ��Ē���
����������B���Ȃ킿��������
�ł���B
����CBessel���̏ꍇ�͂ǂ��Ȃ��Ă��邾�낤�B���𐫂̌����̏ꍇ�ɂ́C
�荇�����i�����������j�ɂ����̌ŗL�������z�ψʂƑz�肵���Ƃ���
���z�d������p���Ă����B�����ł����l�̃A�v���[�`�����݂�B
����Bessel��![]() �́C��(10.149)���邢��
��(10.155)����
�́C��(10.149)���邢��
��(10.155)����
�����Ă���B�����![]() �����z�ψʂƂ��ď悶��
�~�`�����Őϕ�����B�ɍ��W�̔����ʐς�
�����z�ψʂƂ��ď悶��
�~�`�����Őϕ�����B�ɍ��W�̔����ʐς�
![]() ��
���邱�Ƃɒ��ӂ���C���̉��z�d������
��
���邱�Ƃɒ��ӂ���C���̉��z�d������
�Ƃ��Ȃ���Ȃ�Ȃ����Ƃ��킩��B
��ϕ����̑�1���́C�����ϕ����ċ��E�������l�������
�ƂȂ�̂ŁC��̉��z�d������
�ƂȂ�B�����v���Z�X��![]() ��������������������ɓK�p���邽�߂ɁC
�����
��������������������ɓK�p���邽�߂ɁC
�����![]() ���悶�ĉ��z�d������U�������
���悶�ĉ��z�d������U�������
�ƂȂ�B����2�������������ƁC���Ǒ�1, 2���͓����Ȃ̂ŏ����Ă��܂�
�ƂȂ�B�قȂ�ŗL�l���m�͒l���Ⴄ����C�ŏI�I��![]() �̂Ƃ��C
�����Œ�`�������ς�
�̂Ƃ��C
�����Œ�`�������ς�
�Ƃ����W����������B���Ȃ킿�CBessel��������
��L������B
���̓��ς̒�`��(10.140)�Ƃ͎�قȂ�C`![]() '�Ƃ���
�d�݂����ςɂȂ��Ă��邱�Ƃɒ��ӂ���B
'�Ƃ���
�d�݂����ςɂȂ��Ă��邱�Ƃɒ��ӂ���B
�ŏ��̌ŗL�l���ɖ߂�ƁC��(10.148)�̌ŗL����
�ŏI�I��
�̂����ꂩ�Ƃ��ċ��߂�ꂽ���ƂɂȂ�B
���̓�̌ŗL���́C��(10.159)��
��(10.160)�̒��𐫂���C���̓��ς̂��Ƃ�
�̂悤�Ȓ��𐫂�L����B
�����Ă��̌ŗL��
![]() �́C��(10.147)����
�́C��(10.147)����
������B
�ȒP�̂��߁C���炭��![]() �̏�t���Y����S��C���ȗ�����B
�̏�t���Y����S��C���ȗ�����B
���悢�挳�̖��ɖ߂낤�B���߂�ꂽ�ŗL����p���āC����
�Ɖ��肷��B����̉^��������(10.142)�ɑ�������
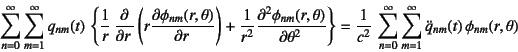
�ƂȂ�B���ӂ̔�ϕ����̒����ʂɎ�(10.163)���������
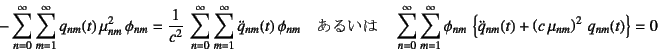
�ƂȂ�B���̗��ӂ�![]() ���悶�ē��ρi���z�d�����j�����߁C
��(10.162)�̒����������l������ƁC
���ǖ��������̒���
���悶�ē��ρi���z�d�����j�����߁C
��(10.162)�̒����������l������ƁC
���ǖ��������̒���![]() ,
, ![]() �̍��݂̂����ɂȂ�
�̍��݂̂����ɂȂ�
���C![]() �ɑ�������������ł���C����
�ɑ�������������ł���C����
�ƂȂ�B���������āC���̖��̈�ʉ���
�ƂȂ�B
�ŏI�I�ɁC����W���͏��������Ō��肳���B��(10.146)�� ��(10.167)���������
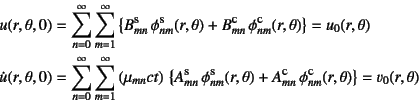
�ƂȂ�B������
![]() ���邢��
���邢��
![]() �Ƃ�
���ς��Ƃ�C��(10.162)�̒����������g����
�Ƃ�
���ς��Ƃ�C��(10.162)�̒����������g����
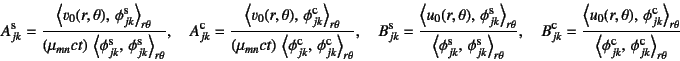
�Ƌ��߂邱�Ƃ��ł���B�}-10.40�ɂ͊e�U�����[�h��
�`�����B�㔼���̋Ȑ���![]() ������
������![]() �̃��[�h�ł���C
��_�������O���ɂ��镔���ł͂���݂����ŁC�����ɂ���ӏ��ł�
���ɂȂ��Ă���ƌ��ė~�����B
�܂�C���̐}�̕��т�2�s�ڂ́C
�̃��[�h�ł���C
��_�������O���ɂ��镔���ł͂���݂����ŁC�����ɂ���ӏ��ł�
���ɂȂ��Ă���ƌ��ė~�����B
�܂�C���̐}�̕��т�2�s�ڂ́C
![]() �܂ł̕�����
���ɂ���ނƂ��ɁC
�܂ł̕�����
���ɂ���ނƂ��ɁC
![]() �̉ӏ��͏�ɕψʂ��邱�Ƃ�
�����Ă���B�܂��C�E�������ɕ`�����̂�
�̉ӏ��͏�ɕψʂ��邱�Ƃ�
�����Ă���B�܂��C�E�������ɕ`�����̂�![]() ������Bessel����
�\���ꂽ���[�h�ł���C���̐}�̉����������̂���݂ƌ��ė~�����B
�Ⴆ��2��ڂ̐}�ł́C���̖������ɂ���ނƂ���
�c��̕����͏�ɕψʂ��邱�Ƃ������Ă���B
������Bessel����
�\���ꂽ���[�h�ł���C���̐}�̉����������̂���݂ƌ��ė~�����B
�Ⴆ��2��ڂ̐}�ł́C���̖������ɂ���ނƂ���
�c��̕����͏�ɕψʂ��邱�Ƃ������Ă���B
�ɂȂ�B
�ɂȂ�B