 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
電子計算機が現在ほど容易には用いることが困難だった時代に多用されていた 応用も含めて,剛性方程式やエネルギ原理等に 関連するもののみを簡単に列挙しておく。
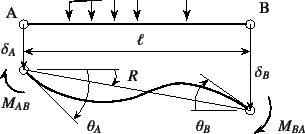
支点沈下が既知の連続梁等の問題では,上で求められた剛性方程式の すべてを用いなくとも不静定モーメントくらいは計算することができる。 従来,このような方法を三連モーメントの定理や四連モーメントの 定理・たわみ角法と称して用いてきた。 このいずれもが梁の要素剛性方程式のうちのモーメントに関するつり合い部分, つまり第2, 4行目の式のみを用いる方法であり,連続梁や対称骨組を 解くのに使われてきた。 例えば図-5.14のような連続梁で,もし節点3にも 支承が配置されていたとすると,まず解く式は節点2, 3のたわみ角を 求める式,すなわち全体剛性方程式のモーメントに関する行である。 したがって,支点沈下が無い場合に一つのスパンを一有限要素で 置き換えたとき,要素剛性方程式のうちの第2, 4行目のみが必要になる。 以下の二つの手法もその二行の式のみを基礎としている。
この公式はまさに剛性方程式の第2, 4行目を並べ替えただけの 式である。 まず,図-5.33のように各不静定モーメント やたわみ角を記すことにする。 記号の正の向きが剛性方程式のそれと異なることに注意しながら 式(5.23)から第2, 4行目を取り出して並べ替えると
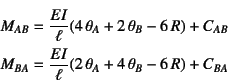
となる。これを用いた解法をたわみ角法
と呼ぶが,
![]() ,
,
![]() ,
,
![]() と定義した。
と定義した。![]() 等は
等価節点外力つまり両端固定の梁に
分布外力が作用したときの不静定反力モーメントであることは
明らかである。
この公式の使い方について,もし知る必要がある場合には,
各種参考書を参照して欲しい。
等は
等価節点外力つまり両端固定の梁に
分布外力が作用したときの不静定反力モーメントであることは
明らかである。
この公式の使い方について,もし知る必要がある場合には,
各種参考書を参照して欲しい。
この定理も同様に,相隣接する二つの要素に対する剛性方程式から
第2, 4行目を取り出して並べ替えたものとして捉えることが
できる。図-5.34に示したような記号と向きで
式(5.23)の第2, 4行目の式をそれぞれの要素に対して
立て,この四つの式から![]() ,
, ![]() ,
,
![]() の三つを消去して誘導される式は
の三つを消去して誘導される式は
となり,三連モーメントの定理
と呼ばれている。ここに![]() および
および![]() が分布外力項,
が分布外力項,![]() は
要素の剛体回転量で,
それぞれ
は
要素の剛体回転量で,
それぞれ
![]() ,
,
![]() ,
,
![]() と定義される。
と定義される。
これに対し,非対称骨組や未知の支点沈下がある問題の場合には, 剛性方程式のうちの用いていない第1, 3行目のせん断力に関する式が必要となる。 そのような場合には,節-5.3.2 (1)で 用いた式(b)の せん断力の連続条件式とこのせん断力に関する剛性方程式部分とを 併せて層方程式 と呼び,同式(b)のモーメントの連続式を節点方程式 と呼び,それを併用して解くことになる。 そうなればもはや,有限要素法の剛性方程式を直接剛性法を 用いて解くのとすべて同じ内容になる。 この使い方についても,もし知る必要がある場合には, 各種参考書を参照して欲しい。
前節までの仮想仕事式は, つり合いを満足している物体各点に仮想の変位を 与えた場合の原理であった。ここではその裏返しの原理を 考えてみる。次の節でそれを用いた簡易解法をいくつか列挙するが, そのような古典的方法だけではなく,例えばハイブリッド有限要素法 のように,応力を未知関数として解く手法を併用するような数値解析法でも 時折用いられる原理であるため,ここにその原理のみを示しておく。 ただし,二つの許容場の使い方には厳密性を若干欠いている。 また簡単のために梁を対象とする。
いま,たわみ![]() と曲げモーメント
と曲げモーメント![]() が
式(4.13b)の
曲げモーメントと曲率の関係を満足しており,
たわみは幾何学的な境界条件を満足している
ものとする。このような場
が
式(4.13b)の
曲げモーメントと曲率の関係を満足しており,
たわみは幾何学的な境界条件を満足している
ものとする。このような場![]() を運動学的許容場
と称している。一方,
この系の分布および端外力を仮想的に変動させたときの内力曲げモーメントの
変動分を
を運動学的許容場
と称している。一方,
この系の分布および端外力を仮想的に変動させたときの内力曲げモーメントの
変動分を![]() と書くと,それは
と書くと,それは
を満足し,変動外力の力学的境界条件も満足している。
このような場![]() を静力学的許容場
と称している。
上の曲げモーメントと曲率の関係にこの仮想的な内力の
変動を乗じて全領域積分し,被積分関数の第1項の部分を2回
部分積分すると
を静力学的許容場
と称している。
上の曲げモーメントと曲率の関係にこの仮想的な内力の
変動を乗じて全領域積分し,被積分関数の第1項の部分を2回
部分積分すると
という関係を得る。右辺第1項は曲率が仮想内力によってされる
仮想的な仕事になっている。第2項目以降もそれと同じように解釈できる。
この
二つの許容場がお互い同じ現象の解(ここが厳密性に欠ける部分)だとすると,
仮想仕事式から全ポテンシャルエネルギを誘導したのと同じ手順を
踏めば,上式から
というスカラー量を定義できることがわかる。
これを補ポテンシャルエネルギ
と呼ぶ。右辺第1項
は補内部ひずみエネルギ と呼ばれる。もちろん この式に曲げモーメントと曲率の関係等を代入して整理すると, 式(5.53)の全ポテンシャルエネルギと形式的には 同じになることは明らかであるが,それを誘導する基礎式が全く 異なっており,厳密には先に述べた二つの許容場を区別して 記さなければならない。 厳密な取り扱いについては文献[115]等を参照のこと。 少しいい加減だが簡単に書けば,補ポテンシャルエネルギが 力を変動させることを前提とした汎関数であるのに対し, 全ポテンシャルエネルギは前節までに用いてきたように, あるつり合い状態から変位を変動させることを 前提とした変位に関する汎関数である。 ただ,前節の全ポテンシャルエネルギの扱いでも二つの 許容場の区別を厳密には行っておらず,少し瞹昧な定義と使い方を している。このあたりも正しくは文献[115]を参照のこと。
ある点![]() に集中外力
に集中外力
![]() が作用してつり合っている
系を考える。デルタ関数の
が作用してつり合っている
系を考える。デルタ関数の![]() と変分の
と変分の![]() とは注意して
区別して欲しい。この同じ系の集中外力
とは注意して
区別して欲しい。この同じ系の集中外力![]() のみを変動させ
た
のみを変動させ
た
![]() に対する
静力学的許容場を用いて,上の式(5.57)の
補仮想仕事の原理を書くと
に対する
静力学的許容場を用いて,上の式(5.57)の
補仮想仕事の原理を書くと
となるから,デルタ関数の定義式(4.55)を
用いると
と書くことができる。ここで,
と考えてもいいから,上式は
という表現もできる。ここに![]() は式(5.59)の
補内部ひずみエネルギである。
この式(5.60)で表される関係をCastiglianoの第2定理
と呼ぶことがある。
は式(5.59)の
補内部ひずみエネルギである。
この式(5.60)で表される関係をCastiglianoの第2定理
と呼ぶことがある。
あるいは,![]() は
は![]() に関しては1次の斉次式であるから
に関しては1次の斉次式であるから
と書いてもよく,これは![]() 点に単位荷重を作用させたときの
同じ系のモーメント分布である。
したがって,式(5.60)の第2式にこれを代入すれば,それは見かけ上
点に単位荷重を作用させたときの
同じ系のモーメント分布である。
したがって,式(5.60)の第2式にこれを代入すれば,それは見かけ上
とも書くことができる。これは単位荷重法 の基礎式(4.58)と 形式的には一致している。ただし単位荷重法の使用例題でも 明らかにしたように,異なる系同士の仮想仕事式として誘導 された単位荷重法の方が汎用性がある。
さて対象としている系に集中外力が作用していない場合にも,
ある架空の集中外力![]() を作用させた場合の静力学的許容場との
積としての式(5.57)が
を作用させた場合の静力学的許容場との
積としての式(5.57)が
となり,ここで
と置くことによって
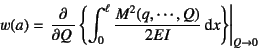
として点![]() のたわみを計算することができる。
のたわみを計算することができる。
例えば図-5.35の(a)のような等分布外力が
作用した片持ち梁先端のたわみを求める場合には,
同じ図(b)のような状態を考える。このモーメント分布は
なので
となり,先端のたわみは上記の定理より
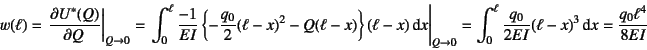
のように,厳密解(4.42)が求められる。
一方,式(5.57)の仮想的な静力学的許容場として,
外力を一定に保ったまま内力![]() だけを変動させたものを
用いるとすると,補仮想仕事の原理には外力補仮想仕事項が
なくなり
だけを変動させたものを
用いるとすると,補仮想仕事の原理には外力補仮想仕事項が
なくなり
となる。したがって前節と同様の考え方をすると,この原理は
とも書くことができる。すなわち,補内部ひずみエネルギ を内力で偏微分したものが零となっている ことから,最小仕事の原理 と呼ばれている。 この原理も前節の定理との混同や同一視がいくつかの文献で見られるが, 論拠となる補仮想仕事の原理が共通しているだけで, 手法としては全く別の概念であることに注意する。
この原理を用いて図-5.36の例を解いてみよう。
曲げ剛性が![]() で伸び剛性が
で伸び剛性が![]() の片持ち梁を,伸び剛性が
の片持ち梁を,伸び剛性が![]() の
ケーブル(トラス)で吊った場合に,梁先端のたわみを
仲介にしてケーブル張力を計算してみよう。この系の内力の一つ
であるケーブル張力を
の
ケーブル(トラス)で吊った場合に,梁先端のたわみを
仲介にしてケーブル張力を計算してみよう。この系の内力の一つ
であるケーブル張力を![]() として,二つの部材を切り離して考えると,
図の右側に示したような載荷状態になる。したがって
として,二つの部材を切り離して考えると,
図の右側に示したような載荷状態になる。したがって
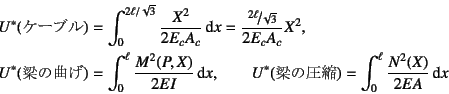
となる。ここに
であるから,上式に代入してその総和を式(5.61)の原理に
代入すると,張力が
と求められる。分母の第2, 3項にある比を
と書くことができる。梁が非常に細長い場合には![]() も
も![]() も
大きくなるため分母の第2, 3項は第1項に比べて無視でき,
ケーブル張力は
も
大きくなるため分母の第2, 3項は第1項に比べて無視でき,
ケーブル張力は![]() になる。あるいは,梁の曲げの剛性に
比較してケーブルの伸び縮み剛性だけが大きく,
になる。あるいは,梁の曲げの剛性に
比較してケーブルの伸び縮み剛性だけが大きく,![]() に関する
第2項だけが無視できる場合には文献[81]の
答と一致する。
に関する
第2項だけが無視できる場合には文献[81]の
答と一致する。
この例題を,つり合い式と変形の整合性だけで解こうとすると,
かなり面倒な演算が必要になるが,微小変位理論の範囲内で
上の解が正しいことを示すことはできる。蛇足ながら
前節で概説したCastiglianoの第2定理との関連を敢えて
述べると,図-5.36右側の分割した系を
別々なものと考え,張力![]() を外力とみなし,それぞれの
系にCastiglianoの第2定理を適用して求められる張力方向の
変位同士を等置したものが,上の最小仕事の原理の
使い方の一つだと考えてもいいのかもしれないが・・・。
を外力とみなし,それぞれの
系にCastiglianoの第2定理を適用して求められる張力方向の
変位同士を等置したものが,上の最小仕事の原理の
使い方の一つだと考えてもいいのかもしれないが・・・。
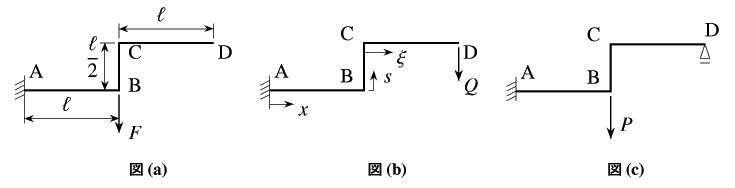
この下に答が書いてあるが,それを見ないでまず上の問題を解いて欲しい。 自分が何回積分したのか確認した上で,以下を読んで欲しい。
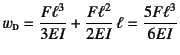 となる。
となる。
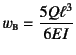 となる。
となる。
![\begin{eqnarray*}
w\subsc{d}&=&\dfrac{Q}{EI}\left[
\int_0^\ell \left(x-2\ell\rig...
...dfrac{\ell^3}{3}-
\ell^3+\ell^3 \right] =\dfrac{19Q\ell^3}{6EI}
\end{eqnarray*}](s2img519.gif)
となる。
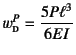 であり,
支点反力
であり,
支点反力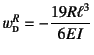 となる。
反力は上向き外力なのでマイナス記号がある。
この和がゼロになることから
となる。
反力は上向き外力なのでマイナス記号がある。
この和がゼロになることから
となる。
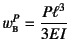 で,
次に,
で,
次に,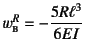 となり,この和から
となり,この和から
となる。
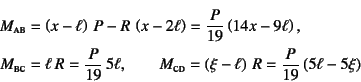
となる。
一方,右端が支えられていない静定系の点Dに右向きに
単位荷重を載せたときの
曲げモーメント分布は
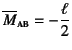 ,
,
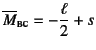 ,
,
![]() となることから,単位荷重法を用いて
となることから,単位荷重法を用いて
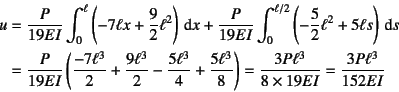
となる。
さて愚痴を書いておきたい。上の問題はある試験で使ったものであるが,
ここで解説したような方法を主に用いた人は皆無であった。
まず1行の足し算で済む問(1)からCastiglianoの第2定理をほとんどの人が使う。
予想はしていたが,問(2) a)や(3) a), b)でも積分ばっかりだったし,
せっかくの積分も計算間違いが少なくなかった。
特に問(3)のa), b)で,積分せずに前問の答を利用したのは
一人か二人だけだったような気がする。
またb)で,エネルギを微分する前に![]() に
に![]() を代入してしまうという
致命的な間違いをした人が数名いた。
力学的な考え方や基本的な数学の理屈が理解されていないようだ。
線形系の重ね合わせは,どこかしら力のつり合いや変形の整合性といった
物理の香りがする数学である。
一方Castiglianoの第2定理を用いた積分には物理の匂いが全くしない。
こういったものが構造力学だと思われてしまうのはちょっとまずいのではないか。
橋を造りたいと思っている人にとっては全然面白くないんじゃないか。
どこが物理でどこが道具の数学か[94]ということを
区別して教えるのはなかなか難しいが,
なんでもかんでも積分というのも問題がある。
を代入してしまうという
致命的な間違いをした人が数名いた。
力学的な考え方や基本的な数学の理屈が理解されていないようだ。
線形系の重ね合わせは,どこかしら力のつり合いや変形の整合性といった
物理の香りがする数学である。
一方Castiglianoの第2定理を用いた積分には物理の匂いが全くしない。
こういったものが構造力学だと思われてしまうのはちょっとまずいのではないか。
橋を造りたいと思っている人にとっては全然面白くないんじゃないか。
どこが物理でどこが道具の数学か[94]ということを
区別して教えるのはなかなか難しいが,
なんでもかんでも積分というのも問題がある。
もちろん自分のことは棚に上げて書いているが, 曲げ理論も習っていないうちから断面の性質(何じゃそりゃ?)と 称して断面2次モーメントを 計算したり,意味も知らずに中立軸を求めたりしたのが 構造力学ではなかっただろうか。 仮想仕事の原理をトラスで教えてもらったような気がするが, 実は単位荷重法とかCastiglianoの定理だったかもしれない。 大学入試のための高校の物理学のように,どういうときにはどの公式を使うかという 記憶科目だったのかもしれない。 本当はどうやって教えるのが一番いいのだろうか。
| つり合い式(4.19) | 構成式(4.13b) | |||
|
方程式(
|
|
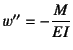 |
共役梁(仮の境界条件)
|
|
| 式(4.23) | ヒンジ | [E1] |
[C1] |
ヒンジ (
|
| 式(4.23) | 固定 | [E2] |
[C2] |
自由 (
|
| 式(4.23) | スライダー | [E3] |
[C3] |
スライダー (
|
| 式(4.23) | 自由 | [E4] |
[C4] |
固定 (
|
| 式(4.23) | 中間支持 | [E5] |
[C5] |
中間ヒンジ (
|
| 式(4.23) | 中間ヒンジ | [E6] |
[C6] |
中間支持 (
|
| 式(4.23) | 中間スライダー | [E7] |
[C7] |
中間スライダー (
|
ついでにもう一つ書いておこう。
上の問題に対する何人かの回答では悪名高いMohrの定理
が使われていた。
これは物理でも数学でもなく,
単に支配方程式が同じ形になっていることを述べているに過ぎない定理である。
とは,文献[111]著者の田村武先生がなにかの講演でおっしゃって
いたことでもあり,その通りである。
くだらない(敢えて書いておこう)定理である。
静定構造であればこの表-5.4の
左半分
![]() で
モーメント分布を求めることができる。
一方この表の右半分
で
モーメント分布を求めることができる。
一方この表の右半分
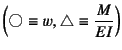 で,
で,![]() ,
,
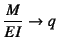 の
置き換えをした上で,境界条件を共役梁
の欄に示したように置き換えさえすれば
(たわみ角のマイナス記号は気にしなくていい),
それは左半分の中の対応する支配方程式に一致する。
つまり,仮の境界条件に置き換えた共役梁に,
求めてあった本当のモーメント分布
の
置き換えをした上で,境界条件を共役梁
の欄に示したように置き換えさえすれば
(たわみ角のマイナス記号は気にしなくていい),
それは左半分の中の対応する支配方程式に一致する。
つまり,仮の境界条件に置き換えた共役梁に,
求めてあった本当のモーメント分布![]() を
仮の分布荷重として載せたときの
仮のモーメント分布を求めれば,それが本当のたわみであるというものである。
この解法は弾性荷重法
と呼ばれているが,どこにも楽しいところが無い。
を
仮の分布荷重として載せたときの
仮のモーメント分布を求めれば,それが本当のたわみであるというものである。
この解法は弾性荷重法
と呼ばれているが,どこにも楽しいところが無い。
ただし,たわみを求めるために力のつり合いを利用していることから, 解くときの頭の中には物理があるのかもしれない。 そういう点ではCastiglianoの定理よりはましかもしれないが, モーメント曲率関係は幾何関係なので,それを力学的に解くことには 意味が無い。 やはり,モーメントを求めた上で微分方程式をきちんと解いた方がいい。 実は上の試験でMohrの定理を使った人の回答の半分は結局, 分布荷重のつり合いの計算,つまり積分で間違ってしまっていた。 やっぱり構造力学は積分の練習科目なのかもしれないな。呵呵。
解析的な解(ここでは敢えて英訳を書いておくがanalytical solution)と 数値(解析)的な解(numerical solution)はもちろん違う。 私の推測では,解析的な解しかなかった時代には, 当たり前だが解析解はそもそも解析的な解だった。 何のことかわからない人の方が多いか。 英語で書くとclosed-formの解,日本語では閉じた解あるいは 陽な解(explicit solution)と直訳するが,そういった解が解析解である。 簡単に言うと,ノートに式で表すことができる解が解析解である。 これに対し, 陰な解(implicit solution: 積分や極限といった作用を含んだものや, 何らかの数値的な計算, 例えば逐次代入法[もう誰も知らないか]や繰り返し計算を 用いないと求められないような解)は,厳密には解析的な解ではないだろう。 が,しかし,それは後述の数値解ではない。というのも, 式の「表現」から直接どのようなパラメータがどう影響するかが把握可能だからだ。 例えば共振曲線の「式(解析的な解)」を見れば(微分すれば) 正確な共振点を求めることが可能だが, 数値解析をして種々の周波数の外力で共振曲線を描いても, 正確な共振点は決して求めることができないことを考えれば, その違いが明らかだ。
さて,コンピュータが広く利用されるようなると, 有限要素法のように計算手法そのものに誤差がある方法も含んで 計算機が出す解を,解析解と区別して数値解と呼ぶようになった。 しかし,数値的に解を求めることを数値解析と呼ぶことから混乱が生まれ, 数値的な解も解析して求められる解だから, つまり実験で求められたものではない解や値だから, それを解析解とか解析値と呼ぶ人達が増えてきたように思う。 特に実験屋さんが間違って使っているような印象がある。 実際に日本人による英語の論文で,実験と数値解析をした研究の 序論に`experimental and analytical studies'とある。 正しくは`experimental and numerical(そうでないならtheoretical)studies'である。 特に解析「値」という言葉を使うようになって混乱は増えたと思う。 数値的な解を,数値解あるいは数値解析解や数値解析値と 呼んでもらえるといいのだが,あるいは 常に「的」をつけたらどうだろう。解析的解と数値的解。 解析的解を求める行為を「解析する」とし, 数値的解を求める行為は「数値解析する」として欲しい。
破壊力学に関する初期の有限要素法の本(例えば[139])を いくつかご執筆になった宮本博東京大学名誉教授の講義に座っていたことがある。 非線形破壊力学だったろうか。全く中身がわからない授業だったが, 授業の中では,有限要素法等の数値解析に変換する「前の」 解析解の大切さを強く説いておられた。 おおいにそうだと思う。 どんなパラメータが答に強い影響を与えるのか調べるという点については, 数値解析にはほとんどメリットは無いからだ。 研究・アプローチの簡単な分類を表-5.5に示した。 真実と事実を区別5.8していることに注意する。 もちろん,この三つのアプローチを網羅した研究が一番望ましいのではあるが。 また最近あるところで気になったのだが,萌芽的研究を除いて工学的研究では, 実証や検証(事実の予測や事実との比較)の無い研究には全く意味が無い。