 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
柱と同様,大きな圧縮力の作用下で平板やシェルが局部座屈 を起こすことは,下敷きやジュースの缶や ペットボトルを圧縮してみればすぐにわかるが, 実際に阪神・淡路大震災時の橋脚等でも多くの局部座屈が発生してしまった。 局部座屈は鋼構造部材の設計に当たって考慮すべき 重要な点である。このような板の安定問題を 解析するために,節-6.4で 定式化した梁-柱理論と同じように, 比較的変位が小さい状態で,平板の安定理論を求めてみよう。 これは通常von Kármánの板理論 と呼ばれている。
図-8.8のように,少したわんだ状態にある
微分要素で断面力の
つり合いを考えよう。
図は見易くなるように,![]() 方向の力と
方向の力と![]() 方向の力に分けてある。
梁-柱理論の誘導でもわかるように,
微小変位理論と異なるのはせん断力のつり合いだけなので,
曲げモーメントは図示していない。さて,せん断力のつり合いをとってみよう。
まず左側の図の
方向の力に分けてある。
梁-柱理論の誘導でもわかるように,
微小変位理論と異なるのはせん断力のつり合いだけなので,
曲げモーメントは図示していない。さて,せん断力のつり合いをとってみよう。
まず左側の図の![]() 方向の力の総和をとり,分布外力
方向の力の総和をとり,分布外力![]() が
無い場合の式(8.18a)を用いると
が
無い場合の式(8.18a)を用いると
![\begin{eqnarray*}
\lefteqn{\left(V_x+\D{V_x}{x}\dint x\right)\dint y-V_x\dint y
...
...uad\qquad
\D{V_x}{x}+N_x \D[2]{w}{x}+N_{xy} \D[2][1][x]{w}{y}
\end{eqnarray*}](s2img1544.gif)
同様に,右側の図の力の総和に![]() 無しの式(8.18b)を
考慮すると
無しの式(8.18b)を
考慮すると
となる。この二つの成分の総和が分布外力![]() とつり合うことに
なり,最終的には
とつり合うことに
なり,最終的には
がせん断力のつり合い式になる。モーメントのつり合い式が 微小変位の範囲での式(8.20)で近似できるのは, 梁-柱理論と同じである。
式(8.20)のモーメントのつり合い式を
式(8.26)に代入してせん断力を消去すると,von Kármánの
平板のつり合い式は
と表すことができる。最初の括弧内が式(8.21)で示される
微小変位理論の枠組内の成分で,次の括弧内が少したわんだ影響,
つまり面内力による付加的なモーメントの影響を表している。
さらに式(8.15)の構成関係をこれに代入すると,
たわみ![]() で表したつり合い式が
で表したつり合い式が
となる。
せん断力についての境界条件にも同様の付加項が
加わる。
![]() の面を例にとると,そのせん断外力に対して
境界でつり合う断面力は,図-8.8左側の左辺に
発生している
の面を例にとると,そのせん断外力に対して
境界でつり合う断面力は,図-8.8左側の左辺に
発生している
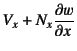 の成分と右図の左辺に
発生している
の成分と右図の左辺に
発生している
![]() との和がその候補である。
一方,
との和がその候補である。
一方,
![]() の
面の場合は
の
面の場合は
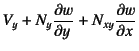 であるだろうことも,
同じ図の奥の辺に発生している内力からわかる。したがって,
それぞれの境界条件は
であるだろうことも,
同じ図の奥の辺に発生している内力からわかる。したがって,
それぞれの境界条件は
となる。 式(8.28)と式(8.18)の面内問題のつり合い式とを連成させ, 与えられた境界条件に対して解けば平板の座屈解析ができることになる。
さて,梁-柱理論の場合においてそうであったように,
この平板の座屈理論でも,面内場のつり合い式は形式的には
線形理論の式(8.18)で表されるが,その
ひずみと変位の関係には,ある程度の非線形項を含むことになる。すなわち
梁-柱理論の式(6.29b)の右辺の表現と同様,
ひずみ成分は変位成分の微係数との間が
という非線形関係で与えられることになる。一方,その面内のつり合い
式(8.18)は形式的に平面問題のつり合い式と一致しているから,
例えば節-3.5.3で紹介したAiryの応力関数
を用いて解くことができる。
つまり式(3.127)と同じように,面内の応力成分がある
応力関数![]() によって
によって
で与えられれば,式(8.8)に式(8.31)を
代入して得る
が,式(8.18)のつり合い式を自動的に満足するのは明らかである。
ここで![]() は曲げの問題から派生する乱れのようなものと考えて,
式(8.30)のひずみ変位関係は面内の
変位成分
は曲げの問題から派生する乱れのようなものと考えて,
式(8.30)のひずみ変位関係は面内の
変位成分![]() ,
, ![]() と面内ひずみの関係であると考えておこう。
すると,微小変位理論の範囲での
平面問題のための適合条件式(3.17)が
ここでも成立すると考えていいから,その左辺に
この式(8.30)を代入して整理すると
と面内ひずみの関係であると考えておこう。
すると,微小変位理論の範囲での
平面問題のための適合条件式(3.17)が
ここでも成立すると考えていいから,その左辺に
この式(8.30)を代入して整理すると
が,この平板の面内問題に対する新しい適合条件
になる。
これに式(8.6)の応力ひずみ関係の
逆関係式(3.114)を代入し,それに
式(8.31)の応力関数で表した応力成分を代入すると,
応力関数![]() は
は
を満足しなければならないことになる。 右辺が零の場合が微小変位理論の式(3.17)で, その場合の応力関数は重調和関数 である。
一方曲げについてのつり合い式に応力関数を導入するために,
式(8.32)を式(8.28)に代入すると,
最終的な曲げに関するつり合い式がたわみ![]() と応力関数
と応力関数![]() で
で
と表されることになる。
この曲げのつり合い式(8.35)と面内問題の
適合条件式(8.34)とを連成させて,![]() および
および![]() に対して,
与えられた境界条件を満たすように解けば,任意の面内力に対する
座屈解析が可能になる。
具体的な解等については参考文献等を参照して欲しい。
に対して,
与えられた境界条件を満たすように解けば,任意の面内力に対する
座屈解析が可能になる。
具体的な解等については参考文献等を参照して欲しい。
もし面内問題について理想的に支持された条件の元で,周辺が
一様な面内圧縮外力で載荷された板の座屈のみを対象とするなら,Airyの
応力関数を用いるまでもなく,一様場の
が面内問題の解と考えていい。
ここに![]() ,
, ![]() はそれぞれ
の方向の面内圧縮外力成分である。
はそれぞれ
の方向の面内圧縮外力成分である。![]() の負の符号は
他の二つの圧縮外力に合わせただけで,特に意味はないが,
曲げを受けてせん断状態にあるプレートガーダのウェブの状態を
モデル化したものに相当する。
この式を式(8.27)に代入すると,
一様に圧縮された
板の比較的大きな変位が生じた状態での板曲げのつり合い式が
の負の符号は
他の二つの圧縮外力に合わせただけで,特に意味はないが,
曲げを受けてせん断状態にあるプレートガーダのウェブの状態を
モデル化したものに相当する。
この式を式(8.27)に代入すると,
一様に圧縮された
板の比較的大きな変位が生じた状態での板曲げのつり合い式が
となる。
もし![]() 方向に無限に
長い板で
方向に無限に
長い板で![]() 方向には一様な外力しか作用せず,端外力も
方向には一様な外力しか作用せず,端外力も![]() のみ
であれば,上式は
のみ
であれば,上式は
となる。これは式(6.27)の梁-柱の
つり合い式と本質的に同じであり,その程度の非線形性を
考慮した理論になっていることが確かめられた。元に戻って,
式(8.37)に式(8.15)のモーメントとたわみ
の関係を代入すると,結局たわみで表したつり合い式は
と書くことができる。
せん断力に関する境界条件は,
式(8.29)を用いて,
式(8.36)の外力条件のもとでは
となる。モーメントに関する境界条件は式(8.24)と同じままである。
最も基本的な例として,図-8.9のように4辺
単純支持された矩形板を,![]() 方向にのみ
一様に圧縮したときの座屈問題を解いておこう。
式(8.38)より,この問題の場合のたわみ
方向にのみ
一様に圧縮したときの座屈問題を解いておこう。
式(8.38)より,この問題の場合のたわみ![]() で
表したつり合い式は
で
表したつり合い式は
となり,境界条件は
でいい。この場合も,Navierの解と同じ様に境界条件を満足する関数で
解を表現してみよう。ここではある一組の三角関数を用いて
と置いてみよう。この関数は明らかに
境界条件式(![]() )を満足している。
式(
)を満足している。
式(![]() )を式(
)を式(![]() )に代入して
整理すると
)に代入して
整理すると
となる。この式が非零の![]() を持つためには,
その係数が零であればいいから,その条件から
それぞれの座屈モード
を持つためには,
その係数が零であればいいから,その条件から
それぞれの座屈モード![]() ,
, ![]() に対する座屈荷重が
に対する座屈荷重が
と求められる。
式(8.40)は,![]() 方向について第
方向について第![]() 次座屈モードで,
次座屈モードで,![]() 方向
について第
方向
について第![]() 次座屈モードの座屈荷重を与えている。
次座屈モードの座屈荷重を与えている。![]() に
関しては
に
関しては![]() のときがこの式の右辺を最小にするので,荷重を零から
単調に増加させたときの最初の座屈荷重は
のときがこの式の右辺を最小にするので,荷重を零から
単調に増加させたときの最初の座屈荷重は![]() のときの
値になる。この分布圧縮座屈荷重を板厚で除して
応力の次元に換算すると
のときの
値になる。この分布圧縮座屈荷重を板厚で除して
応力の次元に換算すると
と定義すると,式(8.41)の座屈応力は
と書くことができる。
したがって,板の座屈強度は
![]() の2乗に
反比例することがわかる。
この
の2乗に
反比例することがわかる。
この
![]() は幅厚比はばあつひ
と呼ばれる寸法比パラメータである。
式(6.36)の梁-柱の
座屈荷重との表現上の比較から明らかなように,
幅厚比は,梁-柱の細長比に
対応する重要なパラメータであることがわかる。
つまりEuler荷重やEuler曲線と特性は同じになる。
基本的にこの式を根拠にした種々の境界条件下の座屈強度から,
フランジ板等の圧縮許容応力や最小板厚等が規定されている。
は幅厚比はばあつひ
と呼ばれる寸法比パラメータである。
式(6.36)の梁-柱の
座屈荷重との表現上の比較から明らかなように,
幅厚比は,梁-柱の細長比に
対応する重要なパラメータであることがわかる。
つまりEuler荷重やEuler曲線と特性は同じになる。
基本的にこの式を根拠にした種々の境界条件下の座屈強度から,
フランジ板等の圧縮許容応力や最小板厚等が規定されている。
一方,
座屈係数の式(8.42)は板の縦横比じゅうおうひ
あるいは辺長
比
![]() の関数になっている。
これを図示したのが図-8.10である。
各縦横比に対して最小の座屈荷重(係数)を与えるモード
の関数になっている。
これを図示したのが図-8.10である。
各縦横比に対して最小の座屈荷重(係数)を与えるモード![]() が
違っている。例えば
が
違っている。例えば
![]() のときの最小の
座屈係数は
のときの最小の
座屈係数は![]() のモードで求められ,
のモードで求められ,![]() となる。
一方,
となる。
一方,
![]() のときの最小の座屈係数は
のときの最小の座屈係数は![]() のモードで
求められ,その座屈係数も
のモードで
求められ,その座屈係数も
![]() のときと同じ
のときと同じ![]() となる。
梁の座屈モードと座屈荷重の関係から考えると,とても妙に感じるが,
これは一体どういうことだろう。この二つの例の
座屈モードを図-8.11に示しておいた。
つまり,二つの正方形が横に並んだ長方形板の最初の座屈は,
それぞれの正方形がそれぞれ独立して,逆の曲率を持って
座屈するのと同じなのだ。
したがって,正方形の座屈荷重と
それを横に2枚並べた長方形の座屈荷重とが一致するのである。
当然,
となる。
梁の座屈モードと座屈荷重の関係から考えると,とても妙に感じるが,
これは一体どういうことだろう。この二つの例の
座屈モードを図-8.11に示しておいた。
つまり,二つの正方形が横に並んだ長方形板の最初の座屈は,
それぞれの正方形がそれぞれ独立して,逆の曲率を持って
座屈するのと同じなのだ。
したがって,正方形の座屈荷重と
それを横に2枚並べた長方形の座屈荷重とが一致するのである。
当然,
![]() のときには
のときには![]() で,やはり同じ最小の
座屈係数
で,やはり同じ最小の
座屈係数![]() になる。
ここでは最も簡単な境界条件の解を示したが,一般的な
場合も式(8.43)の形で座屈荷重を表すのが普通である。
梁-柱の
場合と同様,座屈係数
になる。
ここでは最も簡単な境界条件の解を示したが,一般的な
場合も式(8.43)の形で座屈荷重を表すのが普通である。
梁-柱の
場合と同様,座屈係数![]() が面内外力条件・曲げに関する境界条件・
縦横比の関数として公式集等に与えられている。
が面内外力条件・曲げに関する境界条件・
縦横比の関数として公式集等に与えられている。
さて板の座屈の場合には, 座屈後の変位が梁-柱くらいには大きくならないことが わかっている。 したがって,後座屈挙動についてもvon Kármánの 理論の枠組の中で解を得ることが,ある程度はできる。 ここでは,曲げのつり合い式(8.35)と面内問題の 適合条件式(8.34)とを用いた, 弾性板の1解析例[122]を図-8.12に 示したが,プレートガーダのウェブのように, 面内に曲げを受ける平板の座屈である。 曲げによる面内力は,前節で 紹介したAiryの応力関数を求めることによって,その分布を与えてある。
外力モーメントのレベルが 点Bに至るまでは平板は平面のままを維持するが, この点Bが最初の座屈点であり,安定な経路は板が面外に たわんだ状態つまり実線の方になる。単純な曲げのみを 受けているので,板の上方の2点a, bのたわみと下方の2点c, dの たわみとは異なる挙動を示しているが,それぞれの組は同じ値を持っている。 その後,たわみが板厚の2倍程度に達したときに, 点Aの外力モーメントのレベルで2回目の分岐座屈が 発生する。点Bから点Aまでは,その載荷条件と同様左右対称の 変形モードを板は示しながら面外変形をしているが, 点A以降は左右の対称性も無くなりさらに面外変位が増大していく。 なおこの2回目の座屈外力レベルは,2次モードの座屈荷重レベルよりも 小さいことも興味深い。
ところで膜は,
弦と梁の関係と同様に,
面内張力を受ける平板において曲げ剛性が零になった極限の理論と
考えてよさそうだ。
すなわち式(8.38)で曲げ剛性![]() を零とし,
外力を
を零とし,
外力を
![]() ,
, ![]() と置いた
と置いた
がそのつり合い式
になる。ここに![]() は膜を等方的に
引張っている応力である。
もしこれが運動していれば,Newtonの法則から
は膜を等方的に
引張っている応力である。
もしこれが運動していれば,Newtonの法則から
が運動方程式
になる。ここに![]() は膜の単位表面積当たりの質量であり,
上に付したドットは時間微分である。
さらに分布外力が零であれば,上式は
は膜の単位表面積当たりの質量であり,
上に付したドットは時間微分である。
さらに分布外力が零であれば,上式は
と変形でき,式(3.99)と同じ波動方程式
になる。つまり膜を伝わる波の速度が
であることを示している。ここに![]() は膜の密度である。
式(8.44)は弦の運動方程式(6.85)を2次元に
拡張したものである。
は膜の密度である。
式(8.44)は弦の運動方程式(6.85)を2次元に
拡張したものである。
例えば上フランジに直接輪荷重を載せたとき(あまり 現実味は無いが)の局所的な強度を確かめたいものとする。 ここでは輪荷重は,ある程度小さい面に適切に分布させた表面力だとしよう。 この上フランジをシェル要素でモデル化した上で数値解析をし, 車輪直下で得られた応力を用いてその箇所の上フランジの表面付近の 抵抗挙動を把握できるだろうか。
板厚方向の座標を![]() としておこう。
近頃の汎用プログラムではシェル要素でも
としておこう。
近頃の汎用プログラムではシェル要素でも![]() を求めてくれるのだろうか。
シェルは板と同様,板表面に直接は荷重は載らないし,
板厚方向の応力は零(平面応力)を仮定して構築された理論である。
「おや? 梁に分布外力が載るように,
板やシェルにも分布荷重は載るのでは?」という人は正しい。
しかし,それは板厚中心面上に作用させることになっている。
しかも,それでもなお平面応力状態を仮定してある。
ここが近似力学としての構造力学の面白く不思議なところだ。
汎用プログラムが例えば相当応力を出力してくれたとき,
そこに
を求めてくれるのだろうか。
シェルは板と同様,板表面に直接は荷重は載らないし,
板厚方向の応力は零(平面応力)を仮定して構築された理論である。
「おや? 梁に分布外力が載るように,
板やシェルにも分布荷重は載るのでは?」という人は正しい。
しかし,それは板厚中心面上に作用させることになっている。
しかも,それでもなお平面応力状態を仮定してある。
ここが近似力学としての構造力学の面白く不思議なところだ。
汎用プログラムが例えば相当応力を出力してくれたとき,
そこに![]() が含まれているかどうかを,
皆さんはいつも確かめているのだろうか。
が含まれているかどうかを,
皆さんはいつも確かめているのだろうか。
では上フランジの問題に戻ろう。
実際には直接上フランジの上面に輪荷重が載っているので,
特にウェブ直上ではそれなりに大きな![]() が発生しているはずである。
例えば,
梁の上面に直接荷重が載った場合の図-3.21の
が発生しているはずである。
例えば,
梁の上面に直接荷重が載った場合の図-3.21の![]() を
見れば明らかである。
この応力は,構造部材の有限要素解析ではどこに行ってしまったのだろう。
板曲げによる応力成分
を
見れば明らかである。
この応力は,構造部材の有限要素解析ではどこに行ってしまったのだろう。
板曲げによる応力成分![]() や
や![]() よりも
無視できるくらい小さいのであれば問題は無いが,
果たして目の前の問題はそういう状況にあるのだろうか。
それはシェル要素を用いた有限要素解析をいくらやったって確認できない。
有限要素解析をしてその解を信じる「前に」,何らかの方法を
用いて(頭をちょっと使って)確かめなければならない。
よりも
無視できるくらい小さいのであれば問題は無いが,
果たして目の前の問題はそういう状況にあるのだろうか。
それはシェル要素を用いた有限要素解析をいくらやったって確認できない。
有限要素解析をしてその解を信じる「前に」,何らかの方法を
用いて(頭をちょっと使って)確かめなければならない。