最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• 8.4.1 仮想仕事式
• 8.4.2 変位関数

8.4 剛性方程式

8.4.1 仮想仕事式

Navierの解法で解ける問題は限られているし，級数の収束の問題等， 工学的にも多くの問題がある。そこで章-5で紹介した 有限要素近似を平板に適用しよう。 仮想仕事式 を，つり合い式(8.21)からGaussの 発散定理を用い，式(8.15)の曲げモーメントと 変位の関係式を代入して書き直すと，物理的に意味のある表現として

$$\int_x\int_y D \Biggr[ \left\{\D[2]{w}{x}+\nu\D[2]{w}{y}\right\} \delta\D[2]{w}{x} + \left\{\D[2]{w}{y}+\nu\D[2]{w}{x}\right\} \delta\D[2]{w}{y}$$ (8.25)

$$\qquad\mbox{}+ 2(1-\nu)\D[2][1][y]{w}{x} \delta\D[2][1][y]{w}{x}... ...\dint x \dint y -\int_x\int_y q \delta w\dint x \dint y - \mbox{（境界項）} =0$$

が求められる。別の表現も可能だが，なぜかこの形を使う。 これに変位関数を適切に選んで代入すれば， 平板の要素剛性方程式を求めることができる。

8.4.2 変位関数

物体が2次元の拡がりを持つ場合，変位関数は一般的には

$$w(x,y)=\sum_{0\leq i,j\leq N} \alpha_{ij} x^i y^j$$

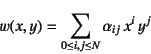
の形で与えられるが，物理的に適切な変位関数であるためには

1. 式(8.25)の表現からみて2階の微係数が存在し
2. 境界条件も併せて考慮すると， 要素の周囲に沿って，1階の微係数が連続つまりたわんだ板の表面が滑らかで
3. 剛体変位を表現できればいい

という条件を満足しなければならない。 実はこの二番目の条件を満足する関数を 選ぶのは困難で，しかも苦労の割には精度がよくないことがわかっている。 例えば長方形要素を用いた場合に，そのたわみの微係数が4隅の節点で 連続するような関数を選べたとしても，要素の辺に沿っても微係数が 連続するとは限らないのである。これは，要素に辺を 持たない棒要素では考える必要の無かった点である。この条件を 満足しない要素は物理的にはおかしいわけだが，逆に， そういった板要素の方が良い結果を与えることがあることも わかっている。このような要素を非適合要素 と呼んでいる。 代表的な適合・非適合要素（古典?）を一つずつ紹介しておこう。

1. Hermite補間式を用いた長方形適合要素: 4隅 の節点で$w$, $\D{w}{x}$, $\D{w}{y}$, $\D[2][1][y]{w}{x}$の四つの自由度を選ぶと，この要素の 総自由度が16となる。表-8.1の 下線で示した項を用いる。
2. Adini-Clough-Meloshの長方形非適合要素: 4隅の 節点で，$w$, $\D{w}{x}$, $\D{w}{y}$の合計12自由度を 選ぶ。表-8.2の下線の項を用いる。

それぞれの特徴やその他の要素についての詳細については 有限要素法に関する多くの参考文献等を参照のこと。

表 8.1: 適合長方形要素の例
表 8.2: 非適合長方形要素の例

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。