最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
章-4では棒の曲げ理論として初等梁理論を定式化したが, 例えば「丸太を縦横に組んだいかだ」のようなものをイメージして, この梁が縦横に多数組み合わさったものとして平板を捉えてみよう。 そうすると,梁に対して観察された現象とほとんど同じような 挙動を平板も示すと予想され,多くの実験から
という二つの基本的な仮定を設けることができることがわかっている。
図-8.1に示した座標系のひずみ成分で この仮定を表現すると
(8.1)
となる。最初の条件式が第1の仮定に,第2, 3式が二番目の 仮定に対応する。 これを式(3.6)のひずみの定義に代入すると 変位成分で表した仮定が
(8.2)
となる。したがって,まず式(8.2a)から
という結論を得る。つまり平板の任意点のたわみは![]() には
依存せず,例えば板厚中心面上(
には
依存せず,例えば板厚中心面上(![]() )でのたわみでその
肉厚方向の任意点のたわみを代表させることができることになる。
この結論を式(8.2b) (8.2c)に代入して,
)でのたわみでその
肉厚方向の任意点のたわみを代表させることができることになる。
この結論を式(8.2b) (8.2c)に代入して,![]() に
関して積分すると
に
関して積分すると
というように,![]() ,
, ![]() 方向の変位成分も,板厚中心面上での変位
成分
方向の変位成分も,板厚中心面上での変位
成分![]() ,
, ![]() ,
, ![]() で表現できることになる。
この形は,式(4.5)で求められていた棒の
変位成分の表現とほとんど同じである。
この結果を示したのが図-8.2である。
このように,3次元物体でありながら,
で表現できることになる。
この形は,式(4.5)で求められていた棒の
変位成分の表現とほとんど同じである。
この結果を示したのが図-8.2である。
このように,3次元物体でありながら,![]() 方向への拡りが他の2方向の
それより極端に小さい平板では,主に
方向への拡りが他の2方向の
それより極端に小さい平板では,主に![]() と
と![]() の関数として変位成分を
捉え,
の関数として変位成分を
捉え,![]() については線形項のみを考慮してやればいいことになる。
このようにして独立変数の数を
減らした近似力学が構造力学である。
については線形項のみを考慮してやればいいことになる。
このようにして独立変数の数を
減らした近似力学が構造力学である。
以上の平板理論の枠組の中での変位成分を,式(3.6)の
ひずみの定義に代入して,零でない他の成分を算定すると
となる。第1, 2式は
曲げを受ける棒のひずみの線形分布式(4.6)と本質的には
同じ表現になっており,平板の板厚中心面の持つそれぞれの方向に
対応する曲率に比例した![]() 方向へのひずみの線形(三角形)分布を
示している。
第3式はこの板厚中心面内でのせん断変形であり,
棒の場合(
方向へのひずみの線形(三角形)分布を
示している。
第3式はこの板厚中心面内でのせん断変形であり,
棒の場合(![]() ,
, ![]() ,
, ![]() )には存在しなかった量である。
)には存在しなかった量である。
棒の場合とは異なり,2次元的に拡った構造系なので,
応力ひずみ関係も1次元のHookeの法則のような
簡単なものは使えない。図-8.1には
平板表面に直接分布外力が作用して
いるように描いてあるが,例えばI形断面梁のウェブのように,
実際の構造部材としての平板表面には
直接外力を直接作用させることは稀である。
さらにここで対象としているのは非常に薄肉の平板であることから,
板内部の![]() 方向の応力成分は他の成分に比べて非常に小さいと
考えていい。したがって平板は平面応力状態にあると
近似・仮定してもよさそうだ。
つまり構成関係は式(3.114)で与えられることになる。
この関係式(3.114)の逆関係
は
方向の応力成分は他の成分に比べて非常に小さいと
考えていい。したがって平板は平面応力状態にあると
近似・仮定してもよさそうだ。
つまり構成関係は式(3.114)で与えられることになる。
この関係式(3.114)の逆関係
は
となるので,これに式(8.5)を代入して
整理すると,応力成分は
のように,変位成分で表すことができる。
もちろん平面応力状態では,
式(3.115a)のように![]() は零ではないはずだが,
平板の最初の板厚不変の仮定式(8.1a)では
は零ではないはずだが,
平板の最初の板厚不変の仮定式(8.1a)では![]() を
零と置き,事実上,平面ひずみ状態も同時に仮定してしまっていることになる。
したがって,式(3.115a)で
を
零と置き,事実上,平面ひずみ状態も同時に仮定してしまっていることになる。
したがって,式(3.115a)で![]() を零に
すると,
を零に
すると,
![]() という
拘束条件をも仮定したことになる。この関係式と
式(3.114)からは,さらに
という
拘束条件をも仮定したことになる。この関係式と
式(3.114)からは,さらに
![]() の
拘束条件も同時に導入してしまったことに相当する。
これは明らかにおかしい。しかしこれも梁理論の場合と同様,
最も重要な直応力分布を精度良く求めるために導入した
仮定から派生する矛盾であり,
ここでも特に注意は払わないことにする。
の
拘束条件も同時に導入してしまったことに相当する。
これは明らかにおかしい。しかしこれも梁理論の場合と同様,
最も重要な直応力分布を精度良く求めるために導入した
仮定から派生する矛盾であり,
ここでも特に注意は払わないことにする。
断面力のうち,棒理論の軸力に対応する平板の面内問題に関する内力は
の三つである。ここに![]() は板厚である。
これに応力と変位の関係式(8.7)を代入すると
は板厚である。
これに応力と変位の関係式(8.7)を代入すると
が三つの断面力と変位成分の関係になる。ここでは
および
という関係を用いている。後者左辺は棒の断面1次モーメントに
対応しており,暗黙のうちに一様な材料でできた板厚中心面上に![]() -
-![]() 面が
あり,その面上で
面が
あり,その面上で![]() が零になるとしているので,
式(8.11)が成立する。
が零になるとしているので,
式(8.11)が成立する。
同様に,梁の曲げモーメントやねじりモーメントに
対応する断面力は
と定義しておけばいい。式(8.11)に注意して,
式(8.7)の応力と変位の関係を式(8.12)に
代入すると
がそれぞれのモーメントと変位成分の関係になる。
ここで,断面2次モーメントに相当する量は単位幅の矩形断面と
して板の断面を考えれば
で定義し,上のモーメントと変位の関係を
と書き表すのが普通である。
最後に,応力を断面力で表現しておく。
式(8.9) (8.15)の表現と
式(8.7)の関係式とを見比べることによって
と表現できることがわかる。単位幅の板の断面積が![]() であるから,
式(4.14)の梁の応力・断面力関係と本質的に同じに
なっている。
さらに断面内板厚方向のせん断応力(仮定の式(8.1b)
(8.1c)からは零になる)に
ついては,節-4.6.1で取り上げたのと
同じ考え方を用い,
求められた直応力につり合う成分として算定しておくと
であるから,
式(4.14)の梁の応力・断面力関係と本質的に同じに
なっている。
さらに断面内板厚方向のせん断応力(仮定の式(8.1b)
(8.1c)からは零になる)に
ついては,節-4.6.1で取り上げたのと
同じ考え方を用い,
求められた直応力につり合う成分として算定しておくと
となる。ここでは単位幅の長方形断面梁内のせん断応力分布として考えて
おり,![]() と
と![]() が梁理論と同様,曲げモーメントの反力と
して,次の節で定義されるせん断力である。
が梁理論と同様,曲げモーメントの反力と
して,次の節で定義されるせん断力である。
以上の六つの断面力の定義を見ながら,
平板の微分要素
![]() に発生している内力の
定義を示したのが図-8.3である。
に発生している内力の
定義を示したのが図-8.3である。![]() と
と![]() は
それぞれ,紙面手前方向あるいは奥行方向のベクトルを表す。
一般化するために,この微分要素に作用している
は
それぞれ,紙面手前方向あるいは奥行方向のベクトルを表す。
一般化するために,この微分要素に作用している![]() ,
, ![]() ,
, ![]() 方向の
分布外力も
方向の
分布外力も![]() ,
, ![]() ,
, ![]() としておいた。
特にモーメントに関して,その2重矢印で示した向きが
座標の正方向を必ずしも指してはいないが,それは
それぞれのモーメントの定義式(8.12)を,
座標の向きとは無関係に
梁の曲げモーメントと同じになるように与えたからである。
また前節の式(8.17)においても述べたように,
曲げに抵抗するであろうせん断力も図には付加してある。
としておいた。
特にモーメントに関して,その2重矢印で示した向きが
座標の正方向を必ずしも指してはいないが,それは
それぞれのモーメントの定義式(8.12)を,
座標の向きとは無関係に
梁の曲げモーメントと同じになるように与えたからである。
また前節の式(8.17)においても述べたように,
曲げに抵抗するであろうせん断力も図には付加してある。
まず図-8.3左側の微分要素の面内力の つり合いは
(8.18)
となる。
この面内のモーメントのつり合いは![]() であり,
連続体のモーメントのつり合い式(3.23)同様,
成立するのが自明なので省略し,式(8.18)でも使ってある。
この式(8.18)は,章-3の
連続体の
であり,
連続体のモーメントのつり合い式(3.23)同様,
成立するのが自明なので省略し,式(8.18)でも使ってある。
この式(8.18)は,章-3の
連続体の![]() ,
, ![]() 方向の
つり合い式(3.21)と形式的に一致している。
このように,面内問題のつり合い式(8.18)は章-3の
連続体のそれと形式的に一致している上に,
実は境界条件も同様になるので,以下,座屈の節までは省略する。
方向の
つり合い式(3.21)と形式的に一致している。
このように,面内問題のつり合い式(8.18)は章-3の
連続体のそれと形式的に一致している上に,
実は境界条件も同様になるので,以下,座屈の節までは省略する。
曲げに関するつり合い式も,図-8.3の
右側に示した微分要素の力とモーメントのつり合いから求めることができる。
まず![]() 方向の力のつり合いから
方向の力のつり合いから
が求められる。この![]() と
と![]() は共に梁理論と同様の考えで
導入したせん断力であり,変形と一対一に対応した断面力ではない。
つまり,板厚面内に発生するせん断応力成分
は共に梁理論と同様の考えで
導入したせん断力であり,変形と一対一に対応した断面力ではない。
つまり,板厚面内に発生するせん断応力成分![]() と
と![]() が
仮定と構成則からは零になるため,その合応力としての
せん断力は零になるはずだが,梁理論と全く同じ理由でこの成分も存在し,
断面にせん断力という内力が発生していると考えることにする。
この部分に疑問を感じる読者は,節-C.3の
数学的誘導を参照して欲しい。
次に
が
仮定と構成則からは零になるため,その合応力としての
せん断力は零になるはずだが,梁理論と全く同じ理由でこの成分も存在し,
断面にせん断力という内力が発生していると考えることにする。
この部分に疑問を感じる読者は,節-C.3の
数学的誘導を参照して欲しい。
次に![]() 軸回りと
軸回りと![]() 軸回りのモーメントのつり合いをとると,
それぞれから
軸回りのモーメントのつり合いをとると,
それぞれから
の2式を得る。これがせん断力![]() ,
, ![]() を定義しているとみなしても
いい。
式(8.20)を式(8.19)に代入して
せん断力を消去すると,最終的に平板の曲げに関するつり合い式
は
を定義しているとみなしても
いい。
式(8.20)を式(8.19)に代入して
せん断力を消去すると,最終的に平板の曲げに関するつり合い式
は
と表現できる。
曲げに関するつり合いの最後の表現式(8.21)に,
モーメントとたわみの関係式(8.15)を代入すると,
板のたわみ![]() で表した曲げに関するつり合い式が
で表した曲げに関するつり合い式が
と求められる。あるいは
という表現になり,![]() のときの解
のときの解![]() が重調和関数
であることを示している。
ちなみに,もし
が重調和関数
であることを示している。
ちなみに,もし![]() 方向に無限に長い平板に
方向に無限に長い平板に![]() 方向には
一様な外力しか作用していない場合には,
方向には
一様な外力しか作用していない場合には,![]() の
の![]() 方向の変化が無いため,
上式での
方向の変化が無いため,
上式での![]() に関する微係数を零としていい。その場合のつり合い式は
に関する微係数を零としていい。その場合のつり合い式は
であるが,もし![]() を無視すれば,最後の式は単位幅の長方形断面の
梁の曲げのつり合い式に一致している。
「梁を丸太のように縦横に組んで板をモデル化する」と前に記したのは,
このような結果に基づいている。
ただし,梁理論には
を無視すれば,最後の式は単位幅の長方形断面の
梁の曲げのつり合い式に一致している。
「梁を丸太のように縦横に組んで板をモデル化する」と前に記したのは,
このような結果に基づいている。
ただし,梁理論には![]() という概念が存在しなかったことには
注意が必要である。節-4.6.3で取り上げた,
幅が広い梁の場合に考慮すべきフランジのせん断遅れ・せん断変形に
関係しているのが,この断面力である。
また円板の曲げの問題の場合には,以上の定式化を極座標で行えば
いいが,上の式から極座標での
という概念が存在しなかったことには
注意が必要である。節-4.6.3で取り上げた,
幅が広い梁の場合に考慮すべきフランジのせん断遅れ・せん断変形に
関係しているのが,この断面力である。
また円板の曲げの問題の場合には,以上の定式化を極座標で行えば
いいが,上の式から極座標での![]() の表現がわかれば,最終的な
つり合い式はやはり式(8.23)で与えられる。
の表現がわかれば,最終的な
つり合い式はやはり式(8.23)で与えられる。
角の存在が![]() の及ぼす奇妙な影響を顕著にしてくれるので,
ここでは矩形板のみを対象とする。
変位を拘束する境界条件は,
梁理論からの類推でも容易にわかるように,たわみやたわみ角を与える
条件である。たわみは
の及ぼす奇妙な影響を顕著にしてくれるので,
ここでは矩形板のみを対象とする。
変位を拘束する境界条件は,
梁理論からの類推でも容易にわかるように,たわみやたわみ角を与える
条件である。たわみは![]() そのものを与える条件になる一方で,
たわみ角は
そのものを与える条件になる一方で,
たわみ角は
![]() の辺上なのか,
の辺上なのか,
![]() の辺なのかで
異なる。これも幾何学的な考察からわかるように
の辺なのかで
異なる。これも幾何学的な考察からわかるように
となる。
力の境界条件はちょっと厄介である。
これも梁理論から類推するとせん断力と曲げモーメントを
規定する二つの条件で表すことができそうだ。
幸い後者は![]() あるいは
あるいは![]() を規定する条件になるが,
前者については注意が必要になる。板の場合の曲げに関する
断面力には,例えば
を規定する条件になるが,
前者については注意が必要になる。板の場合の曲げに関する
断面力には,例えば
![]() の断面ならせん断力
の断面ならせん断力![]() と
曲げモーメント
と
曲げモーメント![]() の他に
の他に![]() が存在する。
この最後の分布ねじりのような断面力
が存在する。
この最後の分布ねじりのような断面力![]() は
境界でどのような成分になっているのだろうか。
文献[126]の解説が一番わかり易いので引用する。
は
境界でどのような成分になっているのだろうか。
文献[126]の解説が一番わかり易いので引用する。
実は,この![]() と
と![]() は,それぞれを独立した境界条件として
与えられる断面力ではないのである。
これをわかり易く示したのが図-8.4である。
これはある
は,それぞれを独立した境界条件として
与えられる断面力ではないのである。
これをわかり易く示したのが図-8.4である。
これはある
![]() の辺の肉厚を眺めたものである。
まず右上の図のように,
せん断力
の辺の肉厚を眺めたものである。
まず右上の図のように,
せん断力![]() は幅
は幅![]() の部分に
の部分に![]() だけ
発生しているだろう。
一方ねじりモーメント
だけ
発生しているだろう。
一方ねじりモーメント![]() は,左上図のように微分要素
は,左上図のように微分要素![]() を
区切って評価すると,図示したような分布をしているが,このモーメントは
そのすぐ下の図のような偶力すなわち
を
区切って評価すると,図示したような分布をしているが,このモーメントは
そのすぐ下の図のような偶力すなわち
![]() といった
力の対によるモーメントとして解釈することができる。
そうすると,二つの微分要素の共有点(図の中央)にはそれぞれの
偶力成分の差である
といった
力の対によるモーメントとして解釈することができる。
そうすると,二つの微分要素の共有点(図の中央)にはそれぞれの
偶力成分の差である
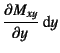 だけの食い違いが,
「せん断力」として生じていると考えていい。
これが右下の図のように,二つの微分要素にまたがる
微分要素
だけの食い違いが,
「せん断力」として生じていると考えていい。
これが右下の図のように,二つの微分要素にまたがる
微分要素![]() に発生している見かけ上のせん断力成分とみなす
ことができる。したがって,せん断力に関する境界条件は,この二つの
せん断力成分の合計で
に発生している見かけ上のせん断力成分とみなす
ことができる。したがって,せん断力に関する境界条件は,この二つの
せん断力成分の合計で
のようになるべきなのである。
モーメントの境界条件は変位のそれと同様,
![]() の
辺上なのか,
の
辺上なのか,
![]() の辺なのかで異なることには注意が必要だが,
最終的には,式(8.20)を考慮して
以上をまとめると,矩形板の境界条件
は
の辺なのかで異なることには注意が必要だが,
最終的には,式(8.20)を考慮して
以上をまとめると,矩形板の境界条件
は
と表現される。ここで示したような誘導は,結果を知っている者だけができる。
したがって,これに疑問を持つ読者は,これも文献[126]を参考にした
数学的な誘導を節-C.3に
示しておいたので,参照して欲しい。
そのような誘導を用いれば,境界条件での![]() の特殊な取り扱いや,
仮定では発生しないせん断力
の特殊な取り扱いや,
仮定では発生しないせん断力![]() と
と![]() の導入に,恣意性を必要としない。
の導入に,恣意性を必要としない。
さて,
このわかり難いねじりモーメント![]() は,もう一つ
おかしな力に深く関係している。というのも,
矩形板のように角を持ちその辺の周方向の幾何形状が
滑らかでない板の場合には,
その角点において不静定反力
が発生するからである。
上の境界条件と同じように
考えると,図-8.5に示したように
板の角の部分では,角を挟む両面でお互いに逆向きの
モーメント
は,もう一つ
おかしな力に深く関係している。というのも,
矩形板のように角を持ちその辺の周方向の幾何形状が
滑らかでない板の場合には,
その角点において不静定反力
が発生するからである。
上の境界条件と同じように
考えると,図-8.5に示したように
板の角の部分では,角を挟む両面でお互いに逆向きの
モーメント![]() が
発生している。このモーメントも上の境界条件での考察と同様,
偶力として取り扱うことにすると,図の右側に示したように
合計
が
発生している。このモーメントも上の境界条件での考察と同様,
偶力として取り扱うことにすると,図の右側に示したように
合計![]() の角反力が発生しているっことになる。
つまり,両辺共に単純支持されている場合,
その角点には
の角反力が発生しているっことになる。
つまり,両辺共に単純支持されている場合,
その角点には![]() だけの支点反力が集中して発生し,
角が跳ね上がったり潜ったりするのを防いでいることになる。
これも数学的な誘導については,節-C.3を参照のこと。
だけの支点反力が集中して発生し,
角が跳ね上がったり潜ったりするのを防いでいることになる。
これも数学的な誘導については,節-C.3を参照のこと。