 |
�ŐV�ł𐳊m�ɓǂޏꍇ�ɂ� pdf �t�@�C�� ���ǂ����B����� web �����̂��߂̊ȈՋ��łł��B
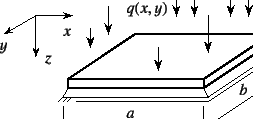
�ł���{�I�ȗ�Ƃ��āC�}-8.6��4�Ӌ���
�P���x�����ꂽ��`�������B
�C�ӂ̕��z�O��![]() ����p������`�̏ꍇ��
����p������`�̏ꍇ��![]() ��
�\���ꂽ�荇�����́C��(8.22)�ŗ^�����Ă���B
���E�����͎�(8.24)����
��
�\���ꂽ�荇�����́C��(8.22)�ŗ^�����Ă���B
���E�����͎�(8.24)����
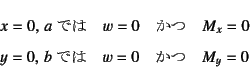
�ƂȂ�B�͂̋��E�����͂ǂ�������[�����g����p���Ă��Ȃ�
�����ŁC���[�����g�ƕψʂ̊W��(8.15)��������ƁC
�Ⴆ��
![]() �̕ӂł�
�̕ӂł�
�ƂȂ�B�������C����
![]() �̕ӏ�ł�
�̕ӏ�ł�![]() ��
��![]() �����ɂ�
�ێ����Ă��邩��
�����ɂ�
�ێ����Ă��邩��![]() �͗�ł���B
���������ď㎮�̑�2���͎����I�ɍl����K�v�������B
���̂悤�ɍl����ƁC�����
�͗�ł���B
���������ď㎮�̑�2���͎����I�ɍl����K�v�������B
���̂悤�ɍl����ƁC�����![]() �ŕ\�������E������
�ŕ\�������E������
�ƍl���Ă����B
��(![]() )�̋��E�����̂��ƂŎ�(8.22)��
�荇�����������������C�����ł͋��E�������������
�p���āC�����
)�̋��E�����̂��ƂŎ�(8.22)��
�荇�����������������C�����ł͋��E�������������
�p���āC�����![]() ��
��
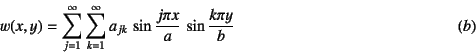
�̂悤�ɋ����ʼn��肷��Bsine����I�̂́C
���E������(![]() )��
���ׂĖ������邩��ł���B��-4.7.2��
���̐U�����������̂ɗp�����ŗL���@�ɂ悭���Ă���B
�i�H�w�I�Ɂj�قƂ�ǂ��ׂĂ̊��炩�Ȋ���Fourier������
�\���ł��邱�Ƃ������ɂ��āC2�dFourier����
�œW�J�����ƍl���Ă������B�����Navier�̉�@
�ƌĂ�ł���B
)��
���ׂĖ������邩��ł���B��-4.7.2��
���̐U�����������̂ɗp�����ŗL���@�ɂ悭���Ă���B
�i�H�w�I�Ɂj�قƂ�ǂ��ׂĂ̊��炩�Ȋ���Fourier������
�\���ł��邱�Ƃ������ɂ��āC2�dFourier����
�œW�J�����ƍl���Ă������B�����Navier�̉�@
�ƌĂ�ł���B
���̉��肵����(![]() )����(8.22)��
�荇�����ɑ�������
)����(8.22)��
�荇�����ɑ�������
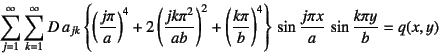
�ƂȂ�B���̗��ӂ�
�Ƃ������Z�i���ς��邢�͉��z�d���̎Z��j���s�����B
����sine���͐�-4.7.2�ł�
�������悤�ɁC�Ⴆ��
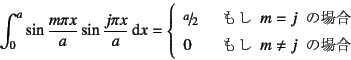
�Ƃ��������i�����j�������Ă���B
���������āC��̐ϕ����Z�����s�����
���ӂ̋����͎���![]() ,
, ![]() �̏ꍇ��1���݂̂����c�炸�C
���͂��ׂė�ɂȂ�B����ČX��
�̏ꍇ��1���݂̂����c�炸�C
���͂��ׂė�ɂȂ�B����ČX��![]() �ɑ���
�ɑ���
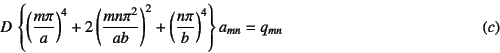
���������Ȃ���Ȃ�Ȃ��B������
�ƒu�����B��(![]() )���
)���
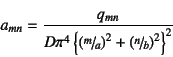
�ƌW���邩��C��(![]() )�ɑ���������Ή���B
���ʓI��
)�ɑ���������Ή���B
���ʓI��![]() �͊�
�͊�![]() ��2�dsine Fourier�W���ɑ�������B
��2�dsine Fourier�W���ɑ�������B
���z�O�͂���l��
![]() �̏ꍇ�ɂ͎�(
�̏ꍇ�ɂ͎�(![]() )���
)���
�ƂȂ�B����������
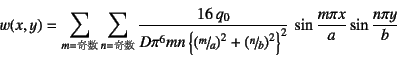
�ƂȂ�B�}-8.7�ɂ�
![]() �ɂ̂�
�ɂ̂�
�̂悤��
�݂��镪�z�O�͂���p�������Ƃ��̓��l�̉����C������
�o��悤�Ɍ֒����Ď����Ă������B�}�ł�![]() ,
, ![]() ���ɋ�����
�ŏ���10���܂łőł��������ʂ�p�����B
���ɋ�����
�ŏ���10���܂łőł��������ʂ�p�����B