最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• 12.7.1 updated Lagrange的数値解析法
• 12.7.2 繰り返し計算と増分計算
  • 12.7.2.1 弾性体モデルの場合
  • 12.7.2.2 弾塑性体モデルの場合
  • 12.7.2.3 単純な増分計算
  • 12.7.2.4 接線剛性は何でもいい

12.7 数値解析

12.7.1 updated Lagrange的数値解析法

ここでは，単純な増分計算に基づく有限要素の定式化について 簡単に整理しておく。まずnominal応力速度で表した 増分つり合い式(12.128)が

$$\dot{n}_{ji,j}+\rho \dot{\pi}_i=0$$

である。これより，対応する仮想仕事式は現配置の体積$v$に対して

$$-\int_{v} \delta v_i \left(\dot{n}_{ji,j}+\rho \pi_i\right... ...\pi_i\right)\dint v -\int_{s} \delta v_i \dot{t}_i \dint s=0$$

となる。構成則では降伏判定等細かい工夫が必要ではあるが， どのようなモデルであっても式(12.126)のnominal応力速度と 速度勾配の間の

$$\dot{n}_{ji}=F_{jikl} v_{k,l}$$

という関係に書き直すことができる。 以上の式は形式的に微小変形理論の仮想仕事式と同じになるので，$\fat{v}$に 適切な多項式を仮定して同様の形状関数も適用した標準的な有限要素の定式化により， 基準配置を$t=t$とする量だけで表した増分剛性方程式

$$\vect{\dot{T}}+\vect{\dot{\Pi}}=\mat{K\subsc{t}} \vect{V}$$

を得る。 $\mat{K\subsc{t}}$が接線剛性行列である。 原則として繰り返し計算を用いずに，この増分剛性方程式を単純に解き， 得られた変位増分$\fat{v}(t)$で節点座標を $\fat{x}(t+\Delta t) \coloneqq\fat{x}(t)+\fat{v}(t)$で更新し， 要素データを新しい $\fat{x}(t+\Delta t)$で再設定する。 応力等の物理量も適切に更新した上で， 次には$t=t+\Delta t$を基準配置にした剛性行列等を 求めて増分計算をさらに継続させていけばいい。 残念ながら，updated Lagrange的表現のためにnominal応力速度を 用いていることから，接線剛性行列が非対称になることには注意する必要がある。 また，要素の形が変形に伴っていびつになることや， 定ひずみ要素でない場合には節点座標の更新だけでは要素の 幾何情報を更新できないことにも注意が必要がある。

12.7.2 繰り返し計算と増分計算

12.7.2.1 弾性体モデルの場合

第1著者が東北大学に赴任したころ，増分表現しかできない 弾塑性問題の数値解析にNewton-Raphson法が用いられている研究を多数見て， 実はかなり動揺した。 そしてそれ以来，種々の論文や発表を通して，少しずつわかってきたような 気がするので，それをまとめておこう。

まず，著者がきちんとしたNewton-Raphson法と呼ぶものの例を示しておこう。 力学とは全く関係は無いが，ある多項式の関数で数値解析をしてみる。 対象とする関数（内力）が

$$f(x,y)\equiv 10 x+x^2y+2xy^2, \quad g(x,y)\equiv 20 y +xy^2+2x^2y, \quad h(x,y)\equiv \dfrac16 \left(xy^3+x^3y\right)$$ (12.196)

と定義されて，問題（つり合い式）は，与えられた$p$, $q$（外力）に対し

$$p=f(x,y)+h(x,y), \quad q=g(x,y)$$ (12.197)

で与えられるものとする。Newton-Raphson法で 第$n$回目の解の改善に用いる接線係数（接線剛性）は

$$\matrx{K_{(n)}}\equiv \left(\begin{array}{cc} \D{(f+h)}{x}\... ...t) & \D{g}{y}\left(x_{(n)}, y_{(n)}\right) \end{array}\right)$$

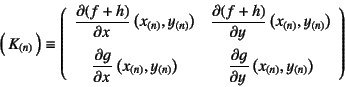
で定義され，改善は

$$\left\{\begin{array}{c} x_{(n+1)} \ y_{(n+1)} \end{array}\... ...h(x_{(n)},y_{(n)}) \ q-g(x_{(n)},y_{(n)}) \end{array}\right\}$$ (12.198)

で行われ，なんらかの誤差が許容範囲に入るまで繰り返すというものだ。 この右辺のベクトルは，第$n$回目の解が持つ不整合な量（不つり合い力）で

$$\left\{\begin{array}{l} p-\left(10 x_{(n)}+x_{(n)}^2y_{(n)}... ...+x_{(n)}y_{(n)}^2+2x_{(n)}^2y_{(n)}\right) \end{array}\right\}$$ (12.199)

と陽に表現できる。 これは式(12.196)で陽に関数が定義されているからで ある。節-E.6.2において極分解の定理を 応用して定式化した弾性梁の 面内有限変位解析法では，増分関係は必要無いことから， 不つり合い力を陽に定式化でき，きちんとしたNewton-Raphson法を 適用できている。ただし，接線剛性は非対称行列になる。

これに対し，例えば増分関係でしか表現できない塑性モデルがこの関数$h$に 含まれている場合をあとで検討しよう。 そのため，ここではまだ元の関数$h$のままで， 増分を用いたNewton-Raphson法を説明しよう。 多分，こういう方法を多くの研究者が用いているのではないかと想像している。 まず$h$の増分は式(12.196)の増分をとることにより

$$\Delta h=\Delta x \dfrac16 \left(y^3+3x^2 y\right) +\Delta y \dfrac16 \left(3xy^2+x^3\right)$$ (12.200)

と求められる。そこで，式(12.199)の代わりに， その不つり合い力を

$$\left\{\begin{array}{l} p-\left(10 x_{(n)}+x_{(n)}^2y_{(n)}... ...+x_{(n)}y_{(n)}^2+2x_{(n)}^2y_{(n)}\right) \end{array}\right\}$$ (12.201)

のような増分で近似計算をすることにしよう。ここに $\Delta h_{(i)}$は 式(12.200)から

$$\Delta h_{(i)}\equiv \Delta x_{(i-1)} \dfrac16 \left(y_{(... ...)} \dfrac16 \left(3x_{(i-1)}y_{(i-1)}^2+x_{(i-1)}^3\right)$$

のようにしてみる。ただし初期値は

$$x_0=0, \quad y_0=0, \quad \Delta x_0=0, \quad \Delta y_0=0$$

とする。 この方法をこの文書では，厳密な（きちんとした）Newton-Raphson法と 区別するために増分Newton-Raphson法と呼ぶことにしよう。 この近似のために，繰り返しの収束半径は小さくなって， 与えられた$(p,q)$に対して， 必ずしも1回で解を得ることができるとは限らなくなる。 そのため，与える量も何回かに分割して 増分 $\left(\Delta p, \Delta q\right)$を与えながら，各増分ステップ毎に 繰り返し収束計算をすることになる。

上の式を用いて解析した例を示してみよう。 与える量の$(p,q)$の組は(250, 200)としておくが，特に意味は無い。 収束判定をする誤差は

$$\sqrt{\dfrac{\Delta x_{(n)}^2+\Delta y_{(n)}^2}{x_{(n)}^2+y_{(n)}^2}} < 10^{-9}$$

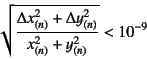
とした。 まず，厳密なNewton-Raphson法の式(12.198)を用いた 場合には， $(p,q)=(250,200)$を ステップ分割せず直接与えても20回以内の繰り返しで解に収束した。 これを$p$と$q$の比は一定にしたまま（比例載荷）で50ステップに分割して 得た解を図-12.24に一点鎖線 （太い実線と重なってしまっている）で示した。 これに対し，増分Newton-Raphson法の式(12.201)で500ステップで 求めたのが実線である。 破線はステップ数を少なくした場合の結果であるが，100ステップで 十分な精度が得られている。

図 12.24: 増分Newton-Raphson法の精度
図 12.25: 弾性体は履歴に非依存

一方図-12.25には，載荷の順序を変えた 場合の結果を実線と破線で示した。一点鎖線が図-12.24の 比例載荷の場合の結果である。実線は$p$を先に，破線は$q$を先に 作用させた場合であるが，式(12.196)からも 明らかなように，$p$を先にしたときは$x$が，$q$を 先にしたときは$y$が線形解として求められている。 しかし，いずれにしても，最終的な $(p,q)=(250,200)$における 解はすべて一致している。 これは，式(12.196)には履歴依存が無いから， つまり$p$と$q$の与え方に依存することが無いからである。

12.7.2.2 弾塑性体モデルの場合

では次に，$h$が増分関係でしか与えられず，$h$そのものを$x$と$y$の 関数として定義することができない場合を対象と してみよう。節-9.2.3で 説明したように，一般には流れ則は積分可能ではないから， その簡便な例をここで示そうとしている。 特に意味は無いが，式(12.200)を大胆にも・・・呵呵

$$\Delta h=\Delta x \dfrac16 \left(y^3+\underline{4}x^2 y\right) +\Delta y \dfrac16 \left(\underline{2}xy^2+x^3\right)$$ (12.202)

と変更してみた。下線を引いた部分の数値は両方共元々は`3'だったから， これを積分して$h(x,y)$を求めることはできず， これがちょうど流れ則に相当する。 つまり，$\Delta h$の「代数和」でしか$h$を計算できない点が， 積分不可能な塑性ひずみ増分を「代数和」で求めることに相当している。 したがって増分Newton-Raphson法でしか解析できない。

図 12.26: 増分関係しか定義できないモデル
図 12.27: 弾塑性体は履歴依存

図-12.26がその結果であるが， $(p,q)=(250,200)$を その比で500ステップで載荷した結果が実線である。 一点鎖線が前節の式(12.200)のモデルの結果である。 破線が50ステップで載荷した場合の結果であるが，このくらいでも 精度はさほど悪くない。増分関係は 大胆に変更したが，最終状態にはあまり違いが出ていないようにも見える。 そこで，載荷の順番を変えた場合の解析をして その結果を図-12.27に示した。 細い実線が図-12.26の比例載荷の結果である。 最終状態は塗りつぶした丸（●）で示してある。 これに対し，破線は$q$を先にしたもので最終状態は白抜き丸（○）。 一点鎖線は$p$を先に載荷して最終状態が四角（□）。 実線は$p$を半分載荷したあと$q$を最後まで載せて， そのあと残りの$p$を載せたもので最終状態は罰点（×）である。 このように，載荷履歴に影響を受けて最終状態が異なり， 塑性の特性をよく現していることがわかる。

12.7.2.3 単純な増分計算

図 12.28: 単純な増分計算

このように，履歴依存の弾塑性モデルの場合はもちろん， そうでないとしても，式(12.131)のように応力の更新のためには ある程度小さい増分の範囲でステップ毎の計算をしなければならないことを 考えると，何も繰り返し計算をしなくてもいいのではないかと， 誰もが考えるだろう。 つまり荷重増分 $\left(\Delta p, \Delta q\right)$に対して単純に

$$\left\{\begin{array}{c} x_{(n+1)} \ y_{(n+1)} \end{array}\... ...ft\{\begin{array}{l} \Delta p \ \Delta q \end{array}\right\}$$

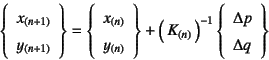
のようにして，増分つり合い式を時々刻々累積して計算したときに生じる 誤差は，増分Newton-Raphson法と同程度ではないかと予想される。 そこで，前節の弾塑性体モデルを，繰り返し無しに，単純に接線剛性を 用いて累積計算してみたのが図-12.28である。 いずれも50ステップで最終状態までを求めてみた。 繰り返し計算の結果を細い線で，単純な増分計算の累積結果を 太い線で描いたのだが，ほとんど重なって見分けがつかない。 また細い破線は，比例載荷の場合を10ステップで計算したものだが， この程度の誤差しか無い。 インセットの図は比例載荷の結果だけを抽出したものである。 このような高い精度の結果が，すべての有限変形理論の枠組の弾塑性解析で 成立するとは考えていないが，しょせん流れ則のような関係と 増分による更新を余儀なくされる解析で，増分つり合い式に基づく 解析には間違いは無く物理的にも十分に意味が有る。

12.7.2.4 接線剛性は何でもいい

もう一つ，第1著者が東北大学に赴任したころに動揺したことがある。 それは「接線剛性は何でもいい」という表現だった。 元を辿ると「修正Newton-Raphson法」という名称で知られている 方法に原因があると想像するが，これは収束繰り返し計算時の最初の接線剛性を 更新せずに用いる方法である。 しかし，弾塑性増分理論においては物理的に意味のある接線剛性を 定義できるため，それを正しく用いるのが望ましい。 それを曖昧に定義すると，繰り返し計算の収束半径が小さくなるだけではなく， 場合によっては収束すらしない可能性も高くなるからだ。 上記の「修正Newton-Raphson法」は，接線剛性を更新はしないものの， 用いる剛性は物理的に正しいものを用いているために問題が生じない。

米国大学大学院ではこのような内容は講義されるが， 我が国では独学なんであろうか。 どちらがいいかわからないが・・・ 文献[59,93]で勉強してみてください。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。