 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
長さ![]() で断面積が
で断面積が![]() の一様な棒の中の,長手方向の熱伝導を
対象とする。
の一様な棒の中の,長手方向の熱伝導を
対象とする。![]() を場所
を場所![]() における時刻
における時刻![]() の温度とし,
断面を通過する単位断面積当りの熱流を
の温度とし,
断面を通過する単位断面積当りの熱流を![]() とする。
符号は,熱が
とする。
符号は,熱が![]() の正方向に流れているときに
の正方向に流れているときに![]() とする。
また,棒の中間部には外からの入熱が単位体積当り
とする。
また,棒の中間部には外からの入熱が単位体積当り![]() だけ
存在するものとする。
多くの実験結果から,材料中に蓄積される単位質量当りの熱は
温度の時間変化率に比例することがわかっていて
だけ
存在するものとする。
多くの実験結果から,材料中に蓄積される単位質量当りの熱は
温度の時間変化率に比例することがわかっていて
となる。ここに![]() は熱容量
であり
は熱容量
であり![]() は密度で,いずれも材料の定数である。
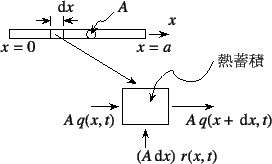
したがって,図-I.1の微分要素の熱(エネルギ)の
保存則から
は密度で,いずれも材料の定数である。
したがって,図-I.1の微分要素の熱(エネルギ)の
保存則から
あるいは
となることから,![]() の極限を考えれば
の極限を考えれば
が熱伝導方程式の基礎になる。
さらにFourierの法則
から,熱流は温度の高いところから低いところに生じることから
という関係になる。ここに![]() は熱伝導率
と呼ばれる材料の定数である。
式(I.3)を式(I.2)に代入すれば,
一般的な熱伝導方程式が
は熱伝導率
と呼ばれる材料の定数である。
式(I.3)を式(I.2)に代入すれば,
一般的な熱伝導方程式が
と求められる。
もし材料が一様であれば,材料の定数は![]() 方向に一定となるため,
上式は
方向に一定となるため,
上式は
と定義されている。
熱伝導方程式は式(I.5)の偏微分方程式で与えられ, これを用いて唯一な未来予測ができるためには, さらに初期条件と境界条件が与えられなければならない。
初期条件は,時刻![]() における棒中の温度分布で与えられるだろうから
における棒中の温度分布で与えられるだろうから
と表される。ここに![]() は時刻
は時刻![]() における任意の場所
における任意の場所![]() の温度分布であり,
未来予測を始める時点で測定する等して与えられる関数である。
の温度分布であり,
未来予測を始める時点で測定する等して与えられる関数である。
さらに,棒の端部の![]() および
および![]() における状態を境界条件として
与えないと,解が唯一にはならない。
境界条件は一般に3種類あるが,最も基本的なものは,
その端部での温度を与える条件(Dirichlet条件あるいは第1種条件
)だろう。つまり
における状態を境界条件として
与えないと,解が唯一にはならない。
境界条件は一般に3種類あるが,最も基本的なものは,
その端部での温度を与える条件(Dirichlet条件あるいは第1種条件
)だろう。つまり
であり,![]() と
と![]() は,
時々刻々端部で測定されている温度を表す与えられる関数である。
は,
時々刻々端部で測定されている温度を表す与えられる関数である。
もう一つの種類は発泡スチロールのような材料で端部を断熱する
条件(Neumann条件あるいは第2種条件
)である。
この場合は,端部での熱流が零になる条件なので
となる。あるいは,外部からの入熱装置を用いて,![]() の正の向きに
指定した熱流を与える条件も考えられ,その場合は
の正の向きに
指定した熱流を与える条件も考えられ,その場合は
となる。![]() と
と![]() が端部の
が端部の![]() の正方向の熱流量を
表した与えられる関数である。
の正方向の熱流量を
表した与えられる関数である。
三つ目の種類の境界条件は,上の二つの混合したもので,
熱伝導問題ではNewtonの冷却法則
という条件(Robin条件あるいは第3種条件または混合条件
)である。それは
のように与えられる。
つまり,端部の熱流はそこの温度に比例する
というもので,![]() や
や![]() ,
,
![]() ,
, ![]() は材料の定数である。
は材料の定数である。
ひとつ,アメリカ合州国Illinois州Evanston,
Northwestern大学Olmstead教授(1980年頃当時)
の`Differential Equations of Mathematical Physics'の
講義ノートに,面白い考察がある。
「逆向きの熱伝導方程式」という話題で,
簡単のために![]() としたときに無限に長い棒での
としたときに無限に長い棒での
| (I.11) |
という,時間の逆向きの熱伝導の問題を
| (I.12) |
の条件で解いたときに,「どんお」![]() が存在するかどうかという問題である。
講義ノートを今読んでも理解できないが,結局,発散しない解が
存在しないことを比較的容易に証明できるようだ。
つまり,時間の逆向きの熱伝導方程式には物理的に意味のある答が無いことが
証明できるというのだ。
逆向きに再生された拡散する煙の映像には違和感を持つと思うが,
それが物理ではないことを数学は証明できるというのだ。
数学はすごい。
が存在するかどうかという問題である。
講義ノートを今読んでも理解できないが,結局,発散しない解が
存在しないことを比較的容易に証明できるようだ。
つまり,時間の逆向きの熱伝導方程式には物理的に意味のある答が無いことが
証明できるというのだ。
逆向きに再生された拡散する煙の映像には違和感を持つと思うが,
それが物理ではないことを数学は証明できるというのだ。
数学はすごい。