最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

• E.7.1 片端を斜面上で支持された棒
  • E.7.1.0.1 固定端の場合:
  • E.7.1.0.2 回転ばね端の場合:
  
  
• E.7.2 リンクで押された棒

E.7 やや不安定な梁-柱の座屈と数値解

E.7.1 片端を斜面上で支持された棒

図 E.6: 片端を斜面上で支持された棒

E.7.1.0.1 固定端の場合:

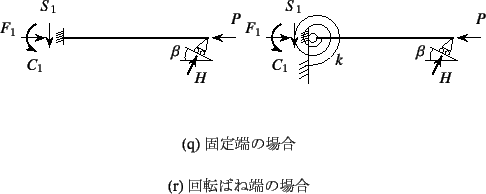
文献[9]にある演習問題であるが，図-E.6の ように右端の支点が斜面に置いてある。 まず図-E.6(a)のように左端が固定されている場合， 反力を図のように定義しておくと，全体のつり合いから

$$F_1=P-H\sin\beta, \quad S_1=H\cos\beta, \quad C_1=-\left(\e... ...beta \underline{\mbox{}+w(\ell) \left(P-H\sin\beta\right)}$$ (E.115)

となる。これを用いて境界条件は，$x=0$で

$$w(0)=0, \quad w'(0)=0, \quad S_1=-\left(-EI w'''(0)-F_1 w'(0)\right), \quad C_1=-\left(-EI w''(0)\right)$$

であり，$x=\ell$では

(E.116)

となる。斜面が無い$\beta=0$のときの$x=\ell$の 境界条件式(E.117a)は，$S_2$を 与えるのではなく$w(\ell)=0$であることに 注意しなければならない。 また，$x=0$の条件は，変位も反力も同時に規定しているように見えることから， 果たして境界条件と呼べるかどうかは疑問ではあるが， 右端が斜面上の支持であることから$w(\ell)$を規定することはできず， したがって反力$H$を陽に含めざるを得ないため，こうなると考えた。 さて，その右端が斜面上の支持であることは，式(E.116)の$C_1$の 右辺の下線・波下線部の二箇所のみにしか現れない。 しかし，波下線部は非線形項であり， 以下の線形固有値解析には含めることができない。 それはつまり，右の支点が斜面上にあるという条件が以下の固有値解析には 含まれないことを示している。

棒の軸力$N$は支点反力$H$の分だけ$P$より減って$F_1$であると考えればいいから， 梁-柱理論の一般解は

$$w(x)=a+bx+c\sin\mu x+d\cos\mu x, \quad \mu\equiv\sqrt{\dfrac{F_1}{EI}}=\sqrt{\dfrac{P-H\sin\beta}{EI}}$$ (E.117)

である。これを境界条件に代入すると， せん断力の条件は左右端で同じ式になり， 結局，残りの五つが$a$〜$d$と$H$に対して

$$a+d=0, \quad b+\mu c=0, \quad \mu^2 b=\dfrac{H}{EI}\cos\beta, \quad c\sin\mu\ell+d\cos\mu\ell=0$$ (E.118)

$$-d\mu^2=-\dfrac{H\ell}{EI}\cos\beta \underline{\mbox{}+ \mu^2 \left\{a+b\ell+c\sin\mu\ell+d\cos\mu\ell \right\}}$$

となるので，$H$を消去して特性方程式を求めると

$$\det\left\vert\begin{array}{cccc} 1 & 0 & 0 & 1 \\ 0 & 1 ... ...ght\vert=\sin\mu\ell \cos\mu\ell- \sin\mu\ell \cos\mu\ell=0$$ (E.119)

となり，明らかに従属な式が並んでいる。つまり，$P$の値， つまり$\mu$の値によらず特性方程式は常に成立している。 これは，右端支点が斜面上にあることを考慮できていないことから， 条件が一つ足りないことを示している。

図 E.7: 座屈モード

そこで，これに対するたわみモードを求めると

$$w(x)=\dfrac{a}{\sin\mu\ell}\left[ \sin\mu\ell-\mu x \cos\mu\ell -\sin\left\{\mu\left(\ell-x\right)\right\} \right]$$ (E.120)

となることから，右端のたわみ$W$は

$$W\equiv w(\ell)=\dfrac{a}{\sin\mu\ell} \left(\sin\mu\ell-\mu\ell\cos\mu\ell\right)$$ (E.121)

となる。図-E.7に，3種類の$\mu\ell$の値に対する モードを描いた。 さて，特性方程式には条件が一つ足りないために それが常に成立してしまうので，不足する条件について検討する必要がある。 そこで，梁-柱はほとんど縮むことができないことから， 座屈する瞬間にはまだ右支点が斜面を登るとは考えられず，$w(\ell)=0$であると 考え，この式(E.122)から座屈の特性方程式を求めると

$$W=0 \quad\to\quad \sin\mu\ell-\mu\ell\cos\mu\ell \quad\to\quad \tan\mu\ell-\mu\ell=0$$ (E.122)

となる。 これは，右端が水平な床にある片端固定・片端単純支持棒の特性方程式と一致する。 ただし，$\mu$の中にも$H$が残り

$$\mu^2=\dfrac{F_1}{EI}=\dfrac{P}{EI}-\dfrac{H}{EI} \sin\beta$$

であり，支点反力$H$は不定のままなので，この特性方程式は解けていない。 また，上の条件から$H=0$は$\cos\mu\ell=0$あるいは$\sin\mu\ell=0$でない限り 自明な解である。 そして右端が何らかの支持をされていることから，$\cos\mu\ell=0$では あり得ない。また外力が固定端に向いていない限り$\sin\mu\ell=0$では あり得ない。したがって，$H\neq 0$でなければならない。 ただし，後述の数値解析でも確かめられるが，座屈する瞬間の 支点反力$H$あるいはせん断力$H\sin\beta$は， 棒の軸力$N$と比較してかなり小さいと考えていいので， 実際には

$$\mu^2=\dfrac{P}{EI}-\dfrac{H}{EI} \sin\beta\simeq \dfrac{P}{EI}$$ (E.123)

と近似していいと予想される。

それならば，モーメントのつり合いにおける右の支点の変位の影響を 無視してもよさそうだ。したがって，式(E.116)の下線部， つまり式(E.119)の下線部を無視すると，その特性方程式は

$$\det\left\vert\begin{array}{cccc} 1 & 0 & 0 & 1 \\ 0 & 1 ... ...0 & -1 \end{array}\right\vert=\mu\ell\cos\mu\ell-\sin\mu\ell=0$$

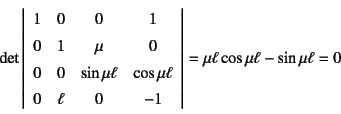
となり，上式(E.123)が得られる。 式(E.116)の下線部を無視したことは，$w(\ell)=0$と 置いたことと同じであるから， 片端固定・片端単純支持棒の特性方程式が得られるのは当然である。

図 E.8: 大変位数値解析
図 E.9: 座屈後の変形

図 E.10: $\beta =15$度の場合の分岐経路
図 E.11: 各段階における変形

そこで，弧長法を用いた有限変位有限要素 （節-E.6.2 (1)参照） で数値解析をしたのが図-E.8である。 細長比はすべて1,000に設定し， 軸の伸び縮みが無いElasticaに近いモデルとした。 図中に示したように，数値解析で与える外力を$P\cos\beta$とみなして 作用させたが，縦軸はそれを$\cos\beta$で割った$P$で 算定してあり，図-E.6(a)の元の問題の$P$と 同じ定義になる。 横軸の$U$は載荷点の水平右向きの変位 $U\equiv u(\ell)$である。 棒は16要素でモデル化したが，座屈をさせるために 一番右端の1要素だけ， $\Delta\beta=\pm 0.5$度だけ さらに傾けてある。$\beta$は図のように反時計回りを正にした。$\beta=0$の場合の 座屈荷重は式(E.123)から $\mu\ell\simeq 4.493$, $\frac{P\ell^2}{EI}\simeq 20.19$なので，$\beta\neq 0$の場合にも ほとんど$\beta$の影響が無いことをこの結果は示している。 これは前述のように，支点反力$H$の影響が非常に小さいからであり， 数値解析でそれが確かめられた。 また，応答が柔らかい方（実験では生じるであろうと 考えられる方）の$\Delta\beta>0$の場合，$\beta$が10度くらいよりも 大きくなると，座屈点は不安定になる。 ちなみに，$\Delta\beta$の符号の違いによる変形形状の 違いを図-E.9に示したが，初期不整に追随した 変形になっている。

$\beta =15$度の場合に，要素数を増やして32要素を用い， 先端の1要素だけを29.9度の傾きにして初期不整を小さくし， 弧長も小さくして求めた最小分岐点からの 分岐経路が図-E.10の実線である。 座屈後はピークまでは安定であった。 一点鎖線は先端の1要素だけを30.1度の傾きにして求めたものである。 図中，a〜gおよびhで示した状態の変形が図-E.11で ある。図-E.10の破線は左の埋め込み端の 棒の軸力$N(0)$であり，座屈荷重レベルでは縦軸の$P$（実線）と 実際の軸力$N$との差が無いことが明らかである。 なお，状態aとc, f, g, hは安定であった。

図 E.12: $\beta =30$度の場合の分岐経路
図 E.13: 各段階における変形

表 E.4: 座屈荷重

$n$	$\mu_n\ell$	$\dfrac{P_n\ell^2}{EI}$
1	4.4934	20.191
2	7.7253	59.680
3	10.904	118.90
4	14.066	197.86
5	17.221	296.55

さらに，$\beta =30$度と大きくして， 最小分岐点からの二つの経路を求めたのが図-E.12で あり，a〜hおよびi, jの状態の変形が図-E.13である。 ここでも32要素を用いて，先端の1要素だけ29.9度の傾きに し，小さめの弧長を用いた。図-E.12の破線は 左の埋め込み端の棒の軸力$N(0)$であり，この場合も座屈荷重レベルでは 縦軸の$P$（実線）と実際の軸力$N$との差が無いことが明らかである。 つまり支点反力$H$が軸力に比べて無視できるほど小さいことを示している。 このことからも，式(E.124)の近似が可能であることを示している。 なお，状態aとjのみが安定であった。 実際の数値解析では，先端の1要素に初期不整として加えた異なる向きの 影響で，まずaの状態に分岐したあと， 順にbからjに至る経路を（偶然，呵呵）計算した。 さて，この図-E.13の 変形形状と図-E.7のモードとを 比較すると，$\mu\ell$が初期座屈点のその値4.493より小さい場合の モードが， $\frac{P\ell^2}{EI}\simeq 20$で荷重低下する方の分岐経路の 一点鎖線の変形形状iやjに似ている。一方，4.493より大きい場合の モードが， $\frac{P\ell^2}{EI}\simeq 20$で荷重増加する方の分岐経路の 実線の変形形状a〜hに似ている。 このように，荷重レベルと変形モードとの関係も整合している。

次に，16要素に戻して$\beta =30$度のまっすぐの棒に大きめの弧長を 用いて載荷した場合の結果が図-E.14である。 ただし，第2分岐経路からの経路（一点鎖線）は， まっすぐの棒のまま分岐直前までを載荷した後， 先端の1要素を0.1度曲げて載荷を続けることに よって求めた。式(E.123)から低次五つの 座屈荷重は表-E.4のように求められる。 このように，実際の実験で多分観察されるであろう最小分岐点からの 不安定な座屈経路以外は，すべて一筆書きのように連続しているのはとても面白い。 この図-E.14に示した記号a〜dの状態での 各変形状態を，それぞれ図-E.15に 示した。図-E.13と比較すれば， 高次モードになっているのが明らかである。 もちろんすべて不安定な状態である。図-E.13の 状態aとiが，1次の座屈における初期不整による安定経路と それに対する不安定経路の組になっており， 安定な状態は右支点付近は上に凸の変形をしている。 同様に，図-E.13の 状態hと，図-E.15の状態dとが，2次の 座屈における初期不整による安定経路とそれに対する不安定経路の 組になっている。この場合も，安定な状態は右支点付近が上に凸の 不自然な変形をしている。

図 E.14: $\beta =30$度のときの高次分岐経路
図 E.15: 高次座屈後の変形

図 E.16: 角度$\beta$が大きい場合
図 E.17: $\beta$が大きい場合の細長比の影響

さて，数値解析における外力を$\cos\beta$で除した$P$と 実際の軸力$N$との座屈点付近の差について 考察するために，もっと角度$\beta$を大きくした場合を 考察する。図-E.16が32要素のまっすぐな棒に対して， この角度$\beta$が90度に近い場合の結果である。 横軸は下の軸が角度の大きい$\beta>88$度の場合の実線に対するもので， 上の軸が$\beta=75$, 80度の一点鎖線に対するものである。 角度$\beta$が88度より小さい場合には， この換算外力$P$で表した座屈荷重は，片端固定・片端単純支持棒の 座屈荷重 $\frac{P\ell^2}{EI}\simeq 20.19$になっている。 また$\beta=75$度の場合には，埋め込み端側の軸力$N$も破線 （図中75($-N$)と記した）で示したが， このくらいの大きな角度であっても，支点反力$H$の影響も含めた 軸力$N$が座屈荷重に至って座屈している。 そして数値結果は，実際に与えた外力を$\cos\beta$で割った 縦軸$P$で表現しても，20.19の荷重レベルで座屈している。 また， $\cos(75\mbox{度})=0.2588$であることから， 横軸が0.4を超える付近から軸力$N$が引張りになるのも当たり前である。 そのあとの変位$U$はもちろん，せいぜい$\ell\cos\beta$の2倍程度までしか 変位できないことになる。

しかし角度$\beta$が88度よりも大きな角度に対する結果を見ると， 上軸のスケールで描いた場合には分岐座屈のように見えてしまうが， 実際にはこの図-E.16のように， ピークを持つ不安定な挙動になっている。 これは，図-E.17の中の対象モデルの図に 示したように， 棒は座屈せずに曲がらないまま縮んで左の方に移動する変形である。 これは棒が縮むために座屈しないで済んでいるので， 軸の伸び縮みを無視したElasticaにもっと近づけるために， 細長比$\lambda$をさらに大きくして再計算したところ， 例えば細長比が10,000より大きい場合には， 式(E.123)で与えられる座屈荷重値 $\frac{P\ell^2}{EI}\simeq 20.19$で分岐座屈した。 逆に細長比を小さくして伸び縮みし易くした場合の 解析結果を図-E.17に示した。 つまり，細長比が10,000より小さい場合には， 座屈せずにほぼまっすぐのまま縮んで左方に変位する。 梁-柱理論も軸方向のひずみは連成させずに解ける 線形理論になっており， その線形座屈解析から得られる結果は，軸ひずみを無視した結果になっているはずだ。 結局，ここの数値解析で細長比をかなり大きくした場合の結果と 線形座屈解析結果はよく整合している。

さて，式(E.120)の特性方程式が不定であったことが 物理的におかしいことを示すために，右端に$e$だけの下方初期変位がある 場合を解いてみる。 この場合には，変位の一般解の係数は次式を満たす必要がある。

$$\bigl( A \bigr)\equiv \left(\begin{array}{cccc} 1 & 0 & 0 &... ...ray}{c} a \ b \ c \ d \end{array}\right\}=\bigl\{y\bigr\}$$ (E.124)

そこで，p.で 述べたAlternative Theoremを用いて解の存在について検討する。 上式(E.125)の付随的 問題である $\bigl( A \bigr)\supersc{t} \bigl\{v\bigr\}= \bigl\{0\bigr\}$の解を求めると， $\bigl\{v\bigr\}= \bigl\lfloor 1 0 1 -1 \bigr\rfloor\supersc{t}$となるので， 初期不整に対して解く問題の右辺と $\bigl\{y\bigr\}\supersc{t} \bigl\{v\bigr\}\neq 0$となり，この代数方程式(E.125)は 解を持たない。逆に， 境界条件式(E.116)で下線部の$w(\ell)$の項を無視した場合には

$$w(x)=\dfrac{-e}{\Delta}\left[ \sin\mu\ell-\mu x \cos\mu\el... ...} \right], \quad \Delta\equiv \mu\ell \cos\mu\ell-\sin\mu\ell$$

これは式(E.121)の $\frac{a}{\sin\mu\ell}$を $\frac{-e}{\Delta}$で 置き換えたものに一致する。 やはり境界条件は，右端で$w(\ell)=0$とするのが正しいのであろうと 考えられる。

E.7.1.0.2 回転ばね端の場合:

図-E.6(b)のような回転ばね支持の場合も同様に反力を定義し， モーメントのつり合いの非線形項を無視すると，その全体のつり合いから

$$F_1=P-H\sin\beta, \quad S_1=H\cos\beta, \quad C_1=-\ell H... ...\beta \underline{\mbox{}+w(\ell) \left(P-H\sin\beta\right)}$$ (E.125)

となる。これを用いて境界条件は，$x=0$で

$$w(0)=0, \quad k w'(0)=-\left(-EI w''(0)\right)=C_1, \quad S_1=-\left(-EI w'''(0)-F_1 w'(0)\right)$$

であり，$x=\ell$では

(E.126)

となる。式(E.127a)は$x=0$のせん断力の条件と同じになるので 考慮する必要がない。 この境界条件に式(E.118)の一般解を代入すると，$H$を消去すれば

$$a+d=0, \quad k\left(b+\mu c\right)+EI \mu^2 d=0, \quad c\sin\mu\ell+d\cos\mu\ell=0$$ (E.127)

$$-d\mu^2=-\ell\mu^2 b^2 \underline{\mbox{}+ \mu^2 \left\{a+b\ell+c\sin\mu\ell+d\cos\mu\ell \right\}}$$

となるので，特性方程式は

$$\det\left\vert\begin{array}{cccc} 1 & 0 & 0 & 1 \\ 0 & \a... ...ght\vert=\sin\mu\ell \cos\mu\ell- \sin\mu\ell \cos\mu\ell=0$$

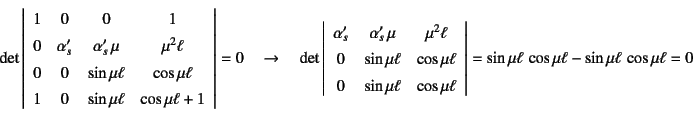
となる。 ここに$\alpha'_s$は，ばね定数$k$と曲げ剛性$EI$の比で

$$\alpha'_s\equiv \dfrac{k\ell}{EI}$$ (E.128)

と定義した。 この場合も，$\mu$の値によらず，また ばね定数$k$の値によらず，特性方程式は常に成立する。 そこで，この場合もたわみを求めると

$$w(x)=\dfrac{a}{\alpha'_s\sin\mu\ell}\left\{ \alpha'_s\left(\... ...\cos\mu\ell\right) +\left(\mu\ell\right)^2\sin\mu\ell\right\}$$

となるので，右端のたわみ $W\equiv w(\ell)$が 零になる条件から座屈の特性方程式は

$$W=0 \quad\to\quad \alpha'_s \left(\mu\ell \cos\mu\ell-\sin\mu\ell\right)- \left(\mu\ell\right)^2\sin\mu\ell=0$$ (E.129)

と求められる。$\alpha'_s$が零のときは両端単純支持棒の 座屈特性方程式$\sin\mu\ell=0$になり，$\alpha'_s$が無限大のときは 片端固定・片端単純支持棒の座屈特性方程式(E.123)に一致する。 そして式(E.130)は，$\mu$の中に未知の$H$を含む ことを除けば，$\beta=0$の水平な床に置かれた 片端回転ばね支持・片端単純支持棒の座屈の特性方程式に形式的には一致する。

次にここでも再度，モーメントのつり合いにおける$w(\ell)$の 影響を無視し，式(E.126)つまり式(E.128)の 下線部を無視すると，特性方程式は

$$\det\left\vert\begin{array}{cccc} 1 & 0 & 0 & 1 \\ 0 & \a... ...u\ell-\sin\mu\ell\right)- \left(\mu\ell\right)^2\sin\mu\ell=0$$

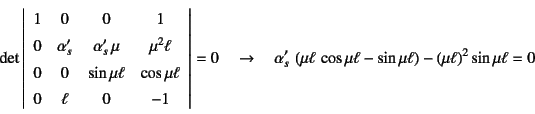
となり，式(E.130)が得られる。

E.7.2 リンクで押された棒

図 E.18: リンクで押された棒
図 E.19: 特性方程式の解

図-E.18の(a)のような，リンクで押された 片持ち棒の問題の場合も， 図のように反力を定義すると，全体のつり合いより

$$F_1=P, \quad S_1=H, \quad C_1=eP-\left(\ell+a\right) H$$

である。境界条件は$x=0$では

$$w(0)=0, \quad w'(0)=0, \quad S_1=EI w'''(0)+P w'(0),\quad C_1=EI w''(0)$$

であり，$x=\ell$では

$$S_2=-EI w'''(\ell)-P w'(\ell)=-H, \quad C_2=-EI w''(\ell)=0$$

となる。これに一般解を代入すると，せん断の境界条件は左右で同じ式になり， 最終的には$a$〜$d$と$H$に対する五つの条件になり，それを解くと

$$w(x)=e \dfrac{\left(1-\cos\mu x\right)\sin\mu\ell+ \left(\... ...{\sin\mu\ell-\mu\ell\left(1+\dfrac{a}{\ell}\right)\cos\mu\ell}$$ (E.130)

と求められる。ただし，ここでは

$$\mu^2\equiv \dfrac{P}{EI}$$

である。そこで，$x=\ell$のたわみを求めると

$$W\equiv w(\ell)=e \dfrac{\sin\mu\ell-\mu\ell\cos\mu\ell}% {\sin\mu\ell-\mu\ell\left(1+\dfrac{a}{\ell}\right)\cos\mu\ell}$$ (E.131)

となる。 したがって，$a=0$のときは分子と分母が同じになるので$w(\ell)=e$である。 座屈荷重については，式(E.131)つまり式(E.132)の 分母が零になる条件から

$$\tan\mu\ell-\mu\ell\left(1+\dfrac{a}{\ell}\right)=0$$

が特性方程式になる。 これは$a=0$のときは，片端固定・片端単純支持棒の座屈荷重の 特性方程式と一致する。 面白いのは，$a\neq 0$のときに，その座屈荷重よりも かなり小さい座屈荷重になるということである。 つまり，図-E.19に示したように，$a=0$なら この解の最小解は $\mu\ell\simeq 4.4934$であるが，$a\neq 0$になった 途端に $0<\mu\ell<\slfrac{\pi}{2}$の間に 解が発生するからである。表-E.5にその 座屈荷重を列挙した。

図 E.20: 大変位数値解析
図 E.21: 解析解と数値解の比較

ここで，先端に $\slfrac{a}{\ell}=\frac14$の長さの リンクが水平から時計回りに2.3度傾いたモデル， つまり $\slfrac{e}{a}=\tan 2.3=0.04016, \slfrac{e}{\ell}=0.01004$で取り付けたモデルを 対象にして数値解析を行った。ここでも細長比は1,000に設定した。 棒は16要素でモデル化し，リンクはどうせ変形しないので1要素とした。 その結果が図-E.20の実線と破線である。 実線は棒端部の下方への変位 $W\equiv w(\ell)$であり， 破線は載荷点の水平右向きの変位 $U\equiv u(\ell+a)$である。 この場合の座屈荷重は表-E.5（図-E.19中にも示した）から $\sqrt{\frac{P\ell^2}{EI}}\simeq 0.7593$， つまり $\frac{P\ell^2}{EI}\simeq 0.5765$になる。 偏心$e$のために， その最初の座屈前から荷重が正の最大値（図中の点A付近）に至るまでは安定で， その後，今度は荷重が負の最大値に至るまでは不安定である。 つまり，支点がヒンジの下にもぐりこんだあと 左に移動してしまうまでは，$P$は次第に小さくなってつり合い， ヒンジ真下の位置を過ぎたところからは$P<0$でブレーキをかけながら変形が進む。 負の最大荷重に至ったあとは，片端固定・片端単純支持棒の座屈に至るまでは 安定である。 つまり，図-E.18の(b)や(c)のように， リンクの部分がくるっと1回転して，載荷支点が棒端部のヒンジよりも 左に移動してしまってから，片端固定・片端単純支持棒の載荷状態に 至るようになるのである。 最初の座屈点付近までの変位$W$の，式(E.132)の解と数値解を 比較したのが図-E.21である。 破線が図-E.20の実線で示した数値解である。 梁-柱理論によって，変位が小さい範囲では精度良く 解が求められていることがわかる。

表 E.5: 座屈荷重

$\dfrac{a}{\ell}$	$\mu\ell$	$\dfrac{P\ell^2}{EI}$
0.05	0.3762	0.1415
0.10	0.5175	0.2678
0.15	0.6175	0.3812
0.20	0.6954	0.4837
0.25	0.7593	0.5765

実際に荷重制御で実験すると，図-E.20の $\frac{% P\ell^2}{EI}\simeq 0.5$レベルに達した 点A付近の状態で，その荷重レベルのまま，$W$は図の右方の$W>0$の 点B付近の解へ，$U$も図のように $U=\slfrac{-\ell}{2}$の点B'付近の解へと 動的に飛び移ることになる。 その後は変位にはあまり変化がなく， 片端固定・片端単純支持棒の座屈荷重 $\frac{P\ell^2}{EI}\simeq 20.19$付近で 再度座屈をする。 ちなみに，図-E.18の(a)のような変形は， 初期状態として右側支点の位置よりも図の下方にヒンジが位置するように 曲がった状態の棒を圧縮した場合に 得ることができるが，棒端部の変位$W$が常に$W>0$な （図-E.20の実線のループが$W>0$側にある） ことを除けば，変形特性は上述の結果とほぼ同じであった。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。