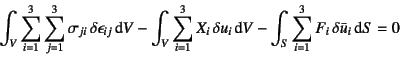最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。

C.1 仮想仕事式

Bernoulli-Eulerの仮定の元で定式化される初等梁理論と， Kirchhoff-Loveの仮定の元で定式化される平板理論とでは， せん断力が内部のせん断応力と定義上は対応しておらず， 一見妙な理論に見えていたと思う。 ここでは仮定に基づく定式化を純粋に実行する[126]ことによって， せん断力が見かけ上の断面力であることを示しておく。 ただもちろん，梁理論や平板理論が，まず直応力を簡便かつ正確に求めるための 近似理論であるということは注記しておきたい。

梁も平板も3次元の空間中の細長いものあるいは薄いものとして捉えればいいので， その仮想仕事式は3次元の式(B.1)と同じであり

$$\int_V \sum_{i=1}^3 \sum_{j=1}^3 \sigma_{ji} \delta \epsi... ... V -\int_{S} \sum_{i=1}^3 F_i \delta \bar{u}_i \dint S = 0$$ (C.1)

でいいことになる。 ここを出発点としよう。

最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。