 |
最新版を正確に読む場合には pdf ファイル をどうぞ。これは web 検索のための簡易旧版です。
第1著者が最も嫌いなもの。 食べても味がしない。 触っても感触が無い。 よく見えないから実は触ることも困難だ。
さて,第2次世界大戦のころ,溶接を用いた橋梁や船舶がいくつか崩壊した。
作用している外力がほぼ無い状態だったため,生じている応力は
かなり小さいと想像された。
金属材料の中に転位という欠陥があることは章-9で述べたが,
転位が結晶界面に移動して延性破壊する応力はある程度高いことがわかっている。
そこで,次のような理想的へき開強度
との比較がなされた。
まず,欠陥の無い結晶構造の金属材料が破断する状況を考えるために,
その結晶格子の原子間に新たに表面を作る(破断させる)のに
必要なエネルギを![]() とする。
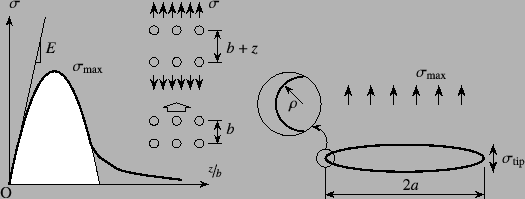
一方,原子間距離と生じる応力の関係は図-F.1の
ようになるため,
この応力と原子間距離の図の面積部分(近似としての図中の網掛け部分)の
エネルギが用いられて表面が生成され,破断するものと考えてみよう。
この図の網掛け部の面積は微小変形の仮定等を用いて近似的に
とする。
一方,原子間距離と生じる応力の関係は図-F.1の
ようになるため,
この応力と原子間距離の図の面積部分(近似としての図中の網掛け部分)の
エネルギが用いられて表面が生成され,破断するものと考えてみよう。
この図の網掛け部の面積は微小変形の仮定等を用いて近似的に
となる。ここに![]() はYoung率であり,
はYoung率であり,![]() は原子間隔である。そして,
そのエネルギが上述の表面生成エネルギ
は原子間隔である。そして,
そのエネルギが上述の表面生成エネルギ![]() (面が2枚あるので)に
達したところで破断が生じると仮定すると,最大応力は
(面が2枚あるので)に
達したところで破断が生じると仮定すると,最大応力は
となる。例えば
![]() くらいだとすると
破断応力は
くらいだとすると
破断応力は
![]() 程度になるが,
具体的な値を鋼を参考にして代入すると
程度になるが,
具体的な値を鋼を参考にして代入すると
となり,
やはりオーダーとしては
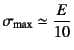 程度となる。
実際の破断応力は
程度となる。
実際の破断応力は
![]() 程度であることから,
この理想的へき開強度で破断していると考えることはできないことがわかる。
程度であることから,
この理想的へき開強度で破断していると考えることはできないことがわかる。
そこでGriffithは,材料中には亀裂
という欠陥が最初から存在し,その先端の応力集中によって
亀裂が進展して破断すると提唱した。
それに基づきOrowanとInglisは,図-F.2に
示したようなとても扁平な楕円形状の空隙が存在する場から,
上述と同様のエネルギ的な概算を行った。
無限遠点に
![]() の応力に相当する荷重が作用している
ときの,楕円空隙の先端付近の応力集中によって拡大された
応力
の応力に相当する荷重が作用している
ときの,楕円空隙の先端付近の応力集中によって拡大された
応力
![]() は
は
程度になる。ここに![]() は楕円空隙の長軸半径であり,
は楕円空隙の長軸半径であり,![]() は
その先端の曲率半径である。ここで非常に扁平な空隙(ほぼ亀裂)であると
すると,上式の第2項の方が第1項よりもかなり大きくなるため,
第1項を無視してもいいことになる。そして,この先端応力が
上述の理想的へき開強度に一致するとすると
は
その先端の曲率半径である。ここで非常に扁平な空隙(ほぼ亀裂)であると
すると,上式の第2項の方が第1項よりもかなり大きくなるため,
第1項を無視してもいいことになる。そして,この先端応力が
上述の理想的へき開強度に一致するとすると
と置くことができる。曲率半径はほぼ結晶格子間隔程度だと
近似(![]() )すれば,上式から
)すれば,上式から
となる。実際に生じている初期亀裂はかなり長いものと
考えて
![]() 程度で
あるとし,
程度で
あるとし,
![]() くらいだとすると
くらいだとすると
のような現実的な値になることがわかる。
したがって,実際に生じた船舶等の崩壊では,亀裂の存在が不可欠であると
考えられるようになった。
このように,亀裂が予め存在する場の挙動を対象とする力学を破壊力学
と呼ぶようになった。
ただここの算定は弾性体としての近似的なモデルに基づくものであり,
実際の亀裂先端の応力はかなり高いことから塑性変形も生じているはずであり,
厳密に破断強度を求めることは困難であることには注意する。
また![]() の極限の空隙を数学的亀裂
と呼ぶ。
の極限の空隙を数学的亀裂
と呼ぶ。